RESOURCE CALC

Teoretisk bakgrunn

innholdsfortegnelse

Innledning

cantilever beam er en av de mest enkle strukturer. Det har bare en støtte, på en av endene. Støtten er en så kalt, fast støtte som hemmer all bevegelse, inkludert vertikale eller horisontale forskyvninger samt eventuelle rotasjoner. Den andre enden er uegnet, og derfor er det gratis å flytte eller rotere. Denne gratis enden kalles ofte tuppen av cantilever.,

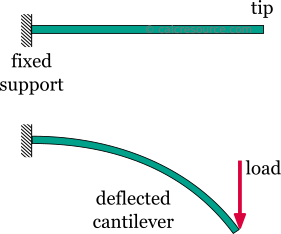
å Fjerne svi støtte eller sette inn en intern hengsel, ville gjengi cantilever bredde til en mekanisme: en kropp som beveger seg uten begrensning i en eller flere retninger. Dette er en uønsket situasjon for en lastbærende struktur. Som et resultat, cantilever bredde tilbyr ingen redundans i form av støtte. Hvis en lokal svikt oppstår hele strukturen ville kollaps., Disse type strukturer, som tilbyr ingen redundans, kalles kritisk eller determinanten strukturer. Det motsatte, en struktur som har mer støtte enn nødvendig for å begrense sin frie bevegelser kalles overflødige eller ubestemte struktur. Den cantilever beam er en determinant struktur.

Forutsetninger

statisk analyse av lastbærende struktur innebærer estimering av sin interne krefter og momenter, så vel som dens deflections., Vanligvis, for et fly struktur, med i flyet legge den interne tiltak av interesse er aksial kraft N , tverrgående skjær kraft V og bøyemoment M . For en cantilever bredde som bærer bare tverrgående laster, den aksial kraft er alltid null, forutsatt at deflections er små. Derfor er det ganske vanlig å overse aksialkreftene.,

De beregnede resultatene på denne siden er basert på følgende forutsetninger:

• material er homogen og isotropic (med andre ord dens egenskaper er de samme i stadig punkt og mot alle retninger
• material er lineær elastisk
• laster anvendes på en statisk måte (de ikke endrer seg med tiden)
• tverrsnitt er den samme på hele bredde lengde
• deflections er små
• Alle tverrsnitt som i utgangspunktet er flyet og også vanlig å lengdeaksen, forblir plane og normal til avledet aksen også., Dette er tilfelle når tverrsnittet høyde er ganske mindre enn bredde lengde (10 ganger eller mer), og også tverrsnitt er ikke multi lagdelt (ikke en sandwich-type-delen).

De to siste forutsetningene tilfredsstille kinematisk krav til Euler Bernoulli stråle teori som er vedtatt her også.

Fortegn

For beregning av interne krefter og momenter på en del kutt av strålen, et tegn konvensjonen er nødvendig., Følgende er vedtatt her:

1. aksial kraft regnes som positive når det fører til spenning til den delen
2. skjær kraft er positive når det fører til en klokke-messig rotasjon av en del.
3. bøyemoment er positive når det fører til spenning til lavere fiber av bredde og komprimering til toppen fiber.

Disse reglene, selv om den ikke er obligatorisk, er ganske universelle. Et annet sett av regler som, hvis de følges konsekvent ville også produsere de samme fysiske resultater.,e, V, og bøyemoment, M

Symboler

• E : materiale elastisitetsmodul (Young ‘ s modulus)
• jeg : treghetsmoment av tverrsnitt rundt elastisk nøytral aksen bøye
• L : total bredde lengde
• R : støtte reaksjon
• d : nedbøyning
• M : bøyemoment
• V : tverrgående skjær kraft
• \theta : helling

Cantilever strålen med ensartet fordelt fyll

load w er fordelt over hele cantilever span, har konstant størrelse og retning., Dens mål er kraft per lengde. Den totale mengden kraft brukt til cantilever bredde er W=w L , der L bredde lengde. Enten det totale kraft W eller distribuert kraft per lengde w kan gis, avhengig av omstendighetene.

følgende tabell inneholder formler som beskriver statisk respons for cantilever bredde under et jevnt fordelt last w .

Cantilever bredde med punkt kraft på spissen

Den makt er konsentrert i ett punkt, som ligger på den frie enden av bjelken., I praksis imidlertid den makt kan være spredt over et lite område, selv om dimensjonene på dette området bør være vesentlig mindre enn cantilever lengde. Like i nærheten av styrken i programmet, stress konsentrasjoner er forventet, og som resultat svar spådd av den klassiske stråle teori er kanskje unøyaktig. Dette er bare et lokalt fenomen, men. Som vi beveger oss bort fra de force beliggenhet, resultatene bli gyldig, i kraft av Saint-Venant prinsippet.,

følgende tabell inneholder formler som beskriver statisk respons for cantilever bredde under et konsentrert punkt kraft P , pålagt på spissen.

Cantilever bredde med punkt kraft på en tilfeldig posisjon

Den makt er konsentrert i ett punkt, hvor som helst over cantilever lengde. I praksis imidlertid den makt kan være spredt over et lite område. For å vurdere styrken som konsentrert, selv om dimensjonene av programmet området bør være vesentlig mindre enn bredde lengde., Like i nærheten av kraft, stress konsentrasjoner er forventet, og som resultat svar spådd av den klassiske bredde teorien kanskje unøyaktig. Dette er bare et lokalt fenomen imidlertid, og som vi beveger oss bort fra de force beliggenhet, spredningen av resultatene blir ubetydelig.

følgende tabell inneholder formler som beskriver statisk respons for cantilever bredde under et konsentrert punkt kraft P , som er pålagt på en tilfeldig avstand fra en fast støtte.,

Cantilever bredde med punkt øyeblikket

I dette tilfellet, et øyeblikk er pålagt i et enkelt punkt av strålen, hvor som helst i hele spennet. I praksis, det kan være en styrke for par, eller et medlem i torsjon, koblet ut av flyet og vinkelrett på strålen.

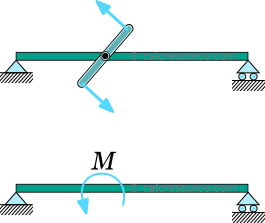
I alle fall, i det øyeblikket programmet området skulle spre seg til et lite lengde av cantilever, slik at det kan være vellykket idealisert som et konsentrert øyeblikk til et punkt., Selv om like i nærheten programmet området, den forventede resultater gjennom den klassiske stråle teori er forventet å være unøyaktige på grunn av stress konsentrasjoner og andre lokale virkninger), den forventede resultater blir helt gyldig, når vi beveger oss bort, som det fremgår av Saint-Venant prinsippet.

følgende tabell inneholder formler som beskriver statisk respons for cantilever bredde under et konsentrert punkt øyeblikket M , som er pålagt på en avstand a fra fast støtte.,

Cantilever strålen med varierende fordelt fyll

lasten er fordelt over hele cantilever lengde, etter å ha lineært varierende størrelse, fra w_1 på fast støtte, for å w_2 på den frie enden. Dimensjonene av w_1 og w_2 er kraft per lengde. Den totale mengden kraft brukt til strålen er W={L\over2}(w_1+w_2) , der L cantilever lengde.

følgende tabell inneholder formler som beskriver statisk respons for cantilever bredde under en varierende fordelt last, av trapesformet form.,

Cantilever strålen med skive-type trapesformet lastfordeling

Dette lastfordeling er typisk for cantilever-bjelker som støtter en skive. Fordelingen ser ut som en rett trapes, med en økende del nærheten til fast støtte og en konstant del, med størrelse lik w , på den gjenværende lengde, opp til tips. Dimensjonene av w er kraft per lengde. Den totale mengden kraft brukt til strålen er W=w (L-a/2) der L er cantilever lengde og, en , er lengden nær fast støtte, hvor lastfordeling er varierende (trekantet).,

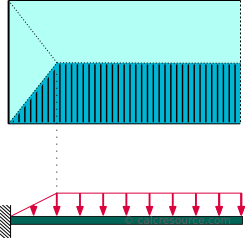
følgende tabell inneholder formler som beskriver statisk respons for cantilever bredde under en trapesformet lastfordeling, på grunn av en skive, som vist i illustrasjon ovenfor.

Cantilever strålen med delvis distribuert uniform fyll

lasten er fordelt til en del av cantilever lengde, med konstant størrelse w , mens de resterende lengde er losset. Dimensjonene av w er kraft per lengde., Den totale mengden kraft brukt til strålen er W=w\venstre(L-a-b\right) , der L cantilever lengde og a , b losset lengder på venstre og høyre side av bjelken, henholdsvis.

følgende tabell inneholder formler som beskriver statisk respons for cantilever bredde under en delvis distribuert jevn belastning.

Cantilever strålen med delvis distribuert trapesformet fyll

lasten er fordelt til en del av cantilever lengde, etter å ha lineært varierende størrelse fra w_1 å w_2 , mens de resterende lengde er losset., Dimensjonene av w_1 og w_2 er kraft per lengde. Den totale mengden kraft brukt til strålen er W={L-a-b\over2}(w_1+w_2) , der L bredde lengde og a , b losset lengder på venstre og høyre side av bjelken henholdsvis.

følgende tabell inneholder formler som beskriver statisk respons for cantilever bredde under en delvis distribuert trapesformet belastning.,