I denne leksjonen skal vi bygge fem (5) felles logisk connectives eller operatører. De er betraktet som vanlige logiske connectives fordi de er svært populære, nyttig og alltid lært sammen.
Før vi begynner, vil jeg foreslå at du leser min andre leksjon i hvor koblingen er vist nedenfor.
Dette innledende leksjon om sannheten tabeller inneholder nødvendige kunnskap eller informasjon som vil hjelpe deg å bedre forstå innholdet i denne leksjonen.,
Introduksjon til Sannheten Tabeller, Uttalelser og Connectives
Le oss starte ved å liste opp de fem (5) felles logisk connectives.
De Fem (5) Felles Logisk Connectives eller Operatører
- Logisk Negasjon
- Logisk Konjunksjon (OG)
- Logiske Motsetninger (Inkludert ELLER)
- Logisk Implikasjon (Betinget)
- Logisk Biconditional (Dobbel Implikasjon)
I., Sannheten Tabell Logisk Negasjon
negasjonen av et utsagn er også en uttalelse med en sannhetsverdi som er akkurat motsatt av den opprinnelige erklæringen. For eksempel, negasjonen av uttrykket er skrevet symbolsk som
~\large{P} eller \large{\neg P}.
~{P} eller {\neg P} leses som «ikke S.»
Husk: negasjon operatør merket med symbolet ~ eller \neg tar sannheten verdi av det opprinnelige utsagnet deretter lagre den motsatte av den sannhet som verdi., Med andre ord, negasjon bare vrenger sannheten verdien av en gitt uttalelse. Dermed, hvis uttalelse P er sann, så er sannheten verdien av dens negasjon er falske. På samme måte hvis P er usann sannheten verdien av dens negasjon er sant.

II. Sannheten Bordet av Logiske Bindeord
En forbindelse er en type sammensatt setning som består av to proposisjoner (også kjent som enkle utsagn) sluttet seg av OG operatør.,
symbolet som brukes for å representere OG eller logisk sammenheng operatøren \color{red}\Large{\kile}. Det ser ut som en omvendt bokstaven V.
Hvis vi har to enkle utsagn P og Q, og vi ønsker å danne en sammensatt setning sammen med det OG operatør, kan vi skrive det slik:
\large{P \kile Q}.
{P \kile Q} leses som «P og Q.»
Husk: sannheten verdi av det sammensatte utsagnet P \kile Q er bare sant hvis sannheten verdier P og Q er både sant., Ellers, S \kile Q er usann.
Merke i sannhet tabellen nedenfor at når P er sann og Q er sanne, S \kile Q er sanne. Imidlertid, de tre andre kombinasjoner av punkter P og Q er usann.

III. Sannheten Tabell Logiske Motsetninger
En motsetninger er en slags sammensatt setning som består av to enkle utsagn dannet ved å bli med i uttalelser med ELLER operatør.
I en motsetninger utsagn, bruk av ELLER er inkluderende. Det betyr at «det ene eller det andre eller begge deler.,
symbolet som brukes for å representere ELLER logiske motsetninger operatøren \color{red}\Large{ \vee }. Det ligner på bokstaven V i alfabetet.
To punkter P og Q sammen med ELLER-operatøren for å danne en sammensatt setning er skrevet som:
\large{P \vee Q}.
{P \vee Q} leses som «P eller Q»
Husk: sannheten verdi av det sammensatte utsagnet P \vee Q er sann hvis sannheten verdi av enten to enkle utsagn P og Q er sanne., Dessuten, S \vee Q er også sant når sannheten verdier av både uttalelser P og Q er sanne. Men, den eneste gangen motsetninger uttalelse P \vee Q er usann, skjer når sannheten verdier av både P og Q er usann.
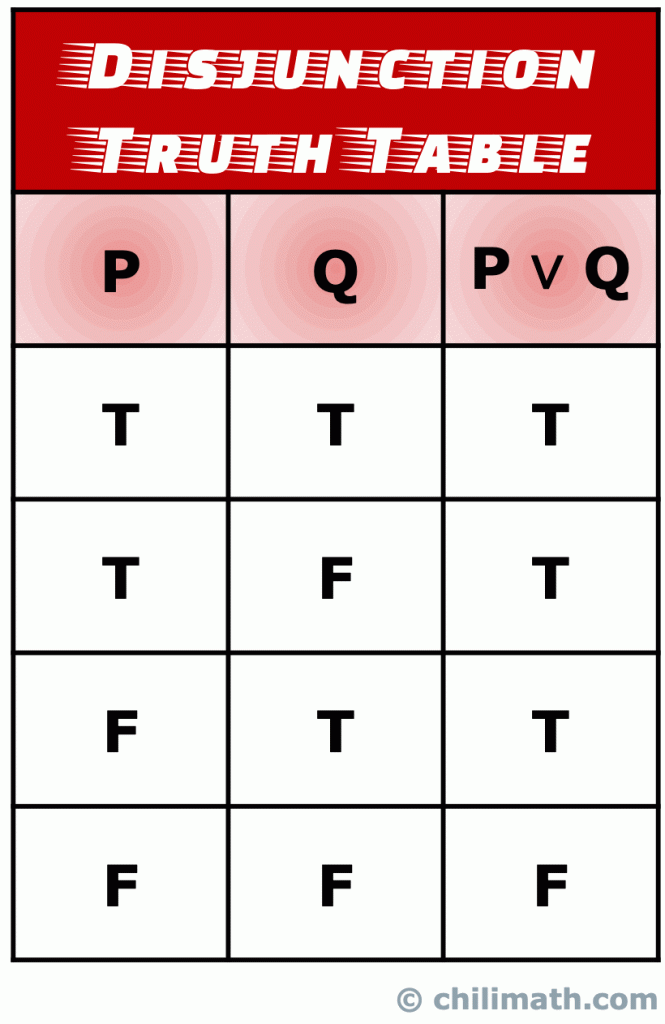
IV. Sannheten Tabell Logiske Implikasjon
En implikasjon (også kjent som et betinget utsagn) er en type sammensatte utsagn som er dannet ved å slå sammen to enkle utsagn med den logiske implikasjon omkringliggende eller operatør.,
symbolet som brukes til å representere den logiske implikasjon operatør er en pil som peker mot høyre, og dermed en pil mot høgre.

Når to enkle utsagn P og Q er koblet sammen med den implikasjon operatør, har vi:
\Large{P \til Q}.
- der P er kjent som hypotese
- hvor Q er kjent som den konklusjon
Det er mange måter å lese betinget {P \til Q}., Nedenfor er noen av de få vanlige.
Husk: sannheten verdi av det sammensatte utsagnet P \til Q er sann når både enkle utsagn P og Q er sanne. Dessuten, S \til Q er alltid sant hvis P er usann. Det eneste scenariet som P \til Q er usann skjer når P er sann og Q er usann.
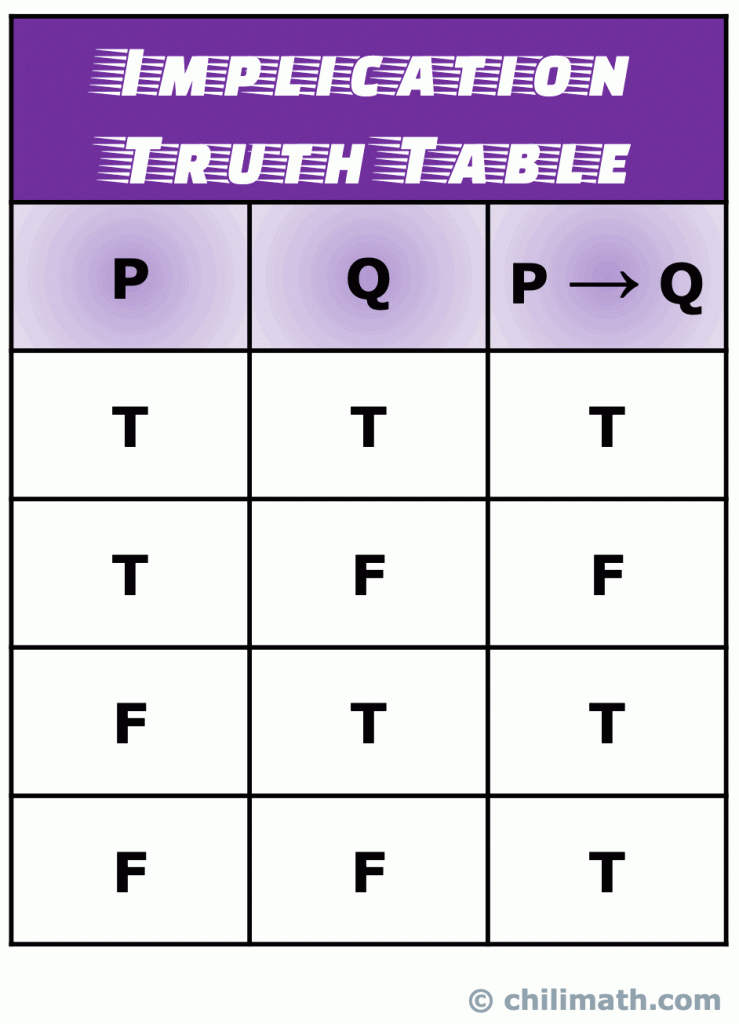
V., Sannheten Tabell Logiske Biconditional eller Dobbeltrom Implikasjon
En dobbel implikasjon (også kjent som en biconditional statement) er en type sammensatte utsagn som er dannet ved å slå sammen to enkle setninger med biconditional operatør. En biconditional uttalelsen er egentlig en kombinasjon av et betinget utsagn og dens snakke.
biconditional operatør er merket med en tohodet pil.,

Når du blir med to enkle setninger (også kjent som molecular utsagn) med biconditional operatør, får vi:
\Large{P \leftrightarrow Q}
{P \leftrightarrow Q} leses som «P hvis og bare hvis Q.,»
- der P er kjent som antecedent
- hvor Q er kjent som en konsekvens
Husk: sannheten verdien av biconditional uttalelse P \leftrightarrow Q er sann når både enkle utsagn P og Q er både sant eller begge forfalskning. Ellers, S \leftrightarrow Q er usann.
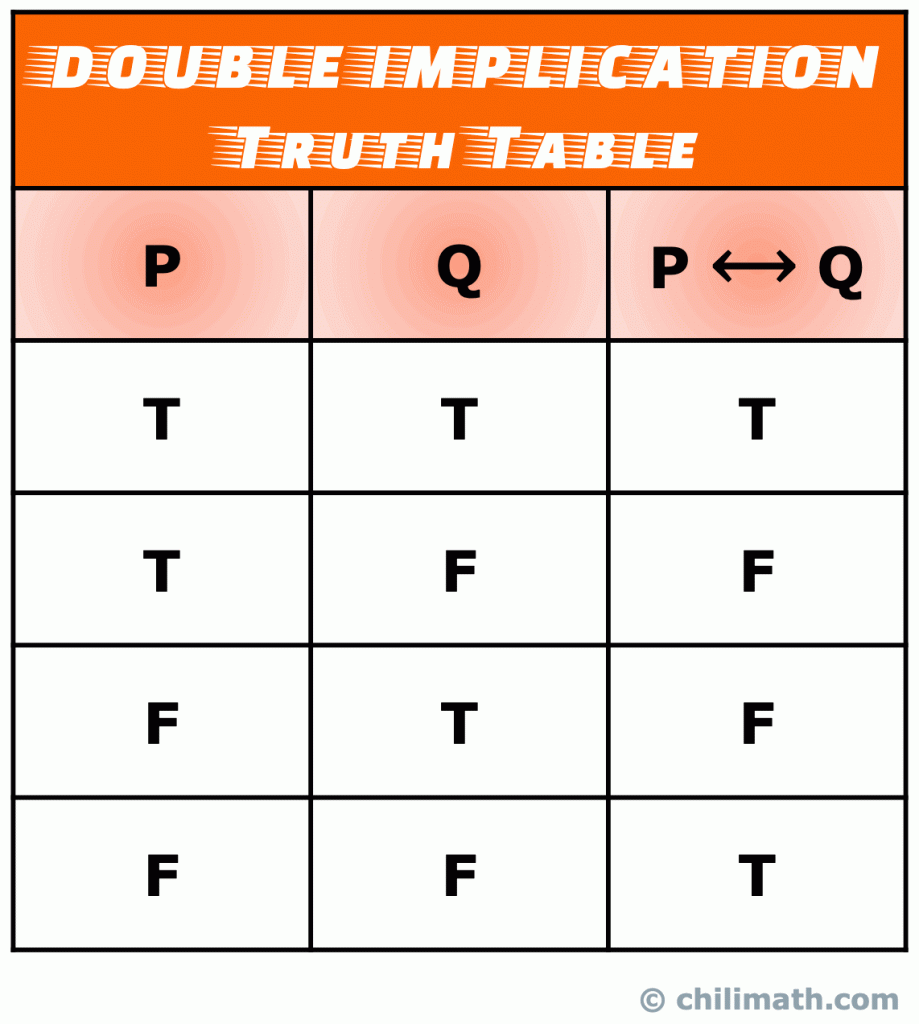
Du kan også være interessert i:
Introduksjon til Sannheten Tabeller, Utsagn og Logiske Connectives
Converse, Invers, og Contrapositive av en Obligatorisk Erklæring
Legg igjen en kommentar