De binomiale verdeling

” Bi “betekent” twee ” (zoals een fiets twee wielen heeft) … … dit gaat over dingen met twee resultaten.,

stel een Muntje!

gooi drie keer een eerlijke munt op … Wat is de kans op twee hoofden?,tr>

THH THT TTH TTT

Which outcomes do we want?,

” twee koppen “kan in elke volgorde zijn:” HHT”,” THH “en” HTH ” hebben allemaal twee koppen (en één staart).

dus 3 van de uitkomsten produceren “twee koppen”.

Wat is de waarschijnlijkheid van elk resultaat?,stellingen zijn (P betekent “Kans”):

• P(Drie Hoofden) = P(HHH) = 1/8
• P(Twee Hoofden) = P(HHT) + P(HTH) + P(THH) = 1/8 + 1/8 + 1/8 = 3/8
• P(Een Hoofd) = P(HTT) + P(THT) + P(TTH) = 1/8 + 1/8 + 1/8 = 3/8
• P(Nul Hoofden) = P(TTT) = 1/8

We schrijven dit in termen van een Random Variabele, X, = “Het getal van de Hoofden van de 3 keer opgooien van een munt”:

• P(X = 3) = 1/8
• P(X = 2) = 3/8
• P(X = 1) = 3/8
• P(X = 0) = 1/8

En dit is hoe het eruit ziet als een grafiek:

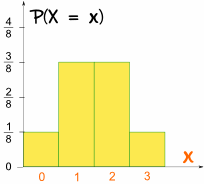
Het is symmetrisch.,

het maken van een formule

stel je nu voor dat we de kans willen hebben op 5 heads in 9 tossen: om alle 512 uitkomsten op te sommen zal lang duren!

dus laten we een formule maken.

in ons vorige voorbeeld, hoe kunnen we de waarden 1, 3, 3 en 1 krijgen ?

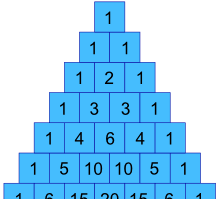
Nou, ze zijn eigenlijk in Pascal ‘ s driehoek !

kunnen we ze maken met behulp van een formule?

zeker kunnen we, en hier is het:

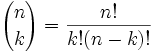
Het wordt vaak genoemd “n choose k”

• n = totaal aantal
• k = aantal dat we willen
• de “!,”betekent ” faculteit”, bijvoorbeeld 4! = 1×2×3×4 = 24

u kunt er meer over lezen bij combinaties en permutaties.

laten we het proberen:

laten we het gebruiken voor een hardere vraag:

Bias!

tot nu toe waren de kansen op succes of mislukking even waarschijnlijk.

maar wat als de munten bevooroordeeld zijn (land meer aan de ene kant dan aan de andere) of keuzes niet 50/50 zijn.

laten we een boomdiagram tekenen:

De “twee kippen” gevallen zijn gemarkeerd.

de kansen voor “twee kippen” zijn allemaal 0,147, omdat we in elk geval twee 0,7 s en één 0,3 vermenigvuldigen. Met andere woorden

0.147 = 0.7 × 0.7 × 0.3

of, gebruikmakend van exponenten:

= 0,72 × 0,31

de 0,7 is de waarschijnlijkheid van elke keuze die we willen, noem het p

de 2 is het aantal keuzes dat we willen, noem het k

en we hebben (tot nu toe):

= pk × 0,31

de 0.,3 is de waarschijnlijkheid van het andere keuze, dus wordt het: 1−p

De 1 is het aantal tegengestelde keuzes, dus het is: n−k

Die ons geeft:

= pk(1-p)(n-k)

Waar

• p de kans is dat elke keuze die we willen
• k is het aantal van de keuzes die we willen
• n is het totaal aantal keuzes

Nu we weten dat de waarschijnlijkheid van elk resultaat is 0.147

OK. Dat was veel werk voor iets wat we al wisten, maar nu hebben we een formule die we kunnen gebruiken voor moeilijkere vragen.,

het samenvoegen

nu weten we hoe we moeten berekenen hoeveel:

n!k!(n-k)!

en de waarschijnlijkheid van elk:

pk(1-p)(n-k)

wanneer we samen vermenigvuldigen krijgen we:

belangrijke opmerkingen:

• de onderzoeken zijn onafhankelijk,
• Er zijn slechts twee mogelijke uitkomsten bij elk onderzoek,
• de kans op “succes” bij elk onderzoek is constant.,

Quincunx

speel met de Quincunx (lees Quincunx uitgelegd) om de binomiale distributie in actie te zien.

gooi de dobbelsteen

een eerlijke dobbelsteen wordt vier keer gegooid. Bereken de kans op het verkrijgen van:

• 0 twee
• 1 twee
• 2 Twee
• 3 Twee
• 4 twee

In dit geval n=4, p = P(twee) = 1/6

X is de willekeurige variabele ‘Aantal twee uit vier worpen’.,

vervang x = 0 tot 4 in de formule:

P (k uit n) = n!k!(n-k)! pk(1-p) (n-k)

op deze manier (tot op 4 decimalen):

Deze keer is de grafiek niet symmetrisch:

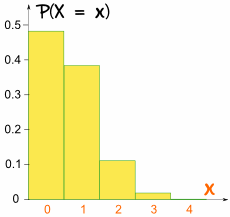
Het is niet symmetrisch!

Het is scheef omdat p niet 0,5

sportfietsen

uw bedrijf maakt sportfietsen. 90% pas definitieve inspectie (en 10% falen en moeten worden vastgesteld).

Wat is het verwachte gemiddelde en de variantie van de volgende vier inspecties?

laten we eerst alle waarschijnlijkheden berekenen.,

• n= 4,
• p = P ( Pass) = 0,9

X is de willekeurige variabele “aantal passes van vier inspecties”.

vervang x = 0 tot 4 in de formule:

P (k uit n) = n!k!(n-k)! pk(1-p) (n-k)

gemiddelde, variantie en standaardafwijking

laten we het gemiddelde, variantie en standaardafwijking voor de inspecties van sportfietsen berekenen.

Er zijn (relatief) eenvoudige formules voor hen. Ze zijn een beetje moeilijk te bewijzen,maar ze werken!,

Het gemiddelde, of “verwachte waarde”, is:

μ = NP

De formule voor variantie is:

variantie: σ2 = np(1-p)

en standaarddeviatie is de vierkantswortel van variantie:

σ = √(np(1-p))