de Stelling van Pythagoras

een van de bekendste wiskundige formules is de Stelling van Pythagoras, die ons de relatie verschaft tussen de zijden in een rechthoekige driehoek. Een rechthoekige driehoek bestaat uit twee poten en een schuine zijde. De twee benen ontmoeten elkaar onder een hoek van 90° en de hypotenusa is de langste zijde van de rechthoekige driehoek en is de zijde tegenover de rechte hoek.,

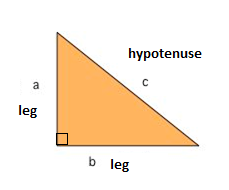
De Stelling van Pythagoras vertelt ons dat de relatie in elke rechthoekige driehoek is:

$$a^{2}+b^{2}=c^{2}$$

Voorbeeld

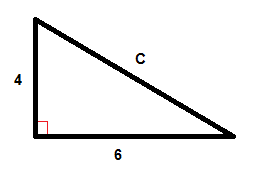
$$C^{2}=6^{2}+4^{2}$$

$$C^{2}=36+16$$

$$C^{2}=52$$

$$C=\sqrt{52}$$

$$C\ca 7.2$$

Er zijn een paar bijzondere soorten rechthoekige driehoeken, zoals de 45°-45° rechts driehoeken en de 30°-60° rechthoekige driehoek.,

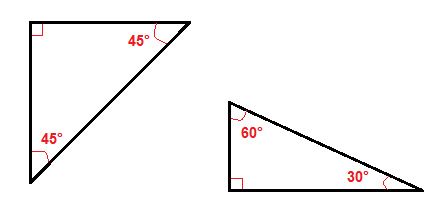
vanwege hun hoeken is het gemakkelijker om de hypotenusa of de poten in deze rechthoekige driehoeken te vinden dan in alle andere rechthoekige driehoeken.

in een rechthoekige driehoek van 45°-45° hoeven we slechts één been met √2 te vermenigvuldigen om de lengte van de hypotenusa te krijgen.

voorbeeld

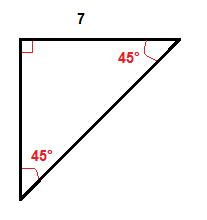
we vermenigvuldigen de lengte van het been dat 7 inches is met √2 om de lengte van de hypotenusa te krijgen.

$$7 \ cdot \ sqrt{2} \ approx 9.,9$$

In een rechthoekige driehoek van 30°-60° kunnen we de lengte van het been vinden dat tegenover de hoek van 30° staat met behulp van deze formule:

$$a=\frac{1}{2}\cdot C$$

voorbeeld

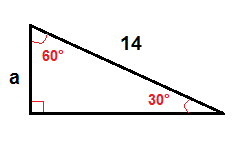
om a te vinden gebruiken we de bovenstaande formule.

$$a=\frac{1}{2}\cdot 14$$

$$a = 7$$

Video les

Zoek de zijden van deze rechthoekige driehoek