de determinant van een matrix is een speciaal getal dat kan worden berekend uit een vierkante matrix.
een Matrix is een array van getallen:
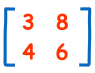
Een Matrix
(Deze heeft 2 rijen en 2 kolommen)
de determinant van die matrix is (berekeningen worden later uitgelegd):
waar is het voor?
de determinant helpt ons de inverse van een matrix te vinden, vertelt ons dingen over de matrix die nuttig zijn in systemen van lineaire vergelijkingen, calculus en meer.,
symbool
Het symbool voor determinant is twee verticale lijnen aan weerszijden.
voorbeeld: <|p>
| A/betekent de determinant van de matrix a
(exact hetzelfde symbool als de absolute waarde.)
het berekenen van de Determinant
Allereerst moet de matrix vierkant zijn (d.w.z. hetzelfde aantal rijen als kolommen hebben). Dan is het gewoon Basis Rekenen., remember when you think of a cross:
- Blue is positive (+ad),
- Red is negative (−bc)
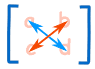
Example:
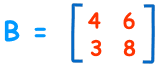
For a 3×3 Matrix
For a 3×3 matrix (3 rows and 3 columns):
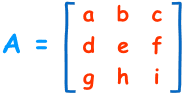
The determinant is:
|A| = a(ei − fh) − b(di − fg) + c(dh − eg)
“The determinant of A equals .,.. etc ”
Het kan ingewikkeld lijken, maar er is een patroon:
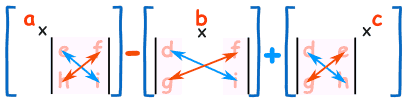
om de determinant van een 3×3 matrix uit te werken:
- vermenigvuldig a met de determinant van de 2×2 matrix die niet in de rij of kolom van a staat.
- hetzelfde voor b, en voor c
- Som ze op, maar onthoud de min voor de b
als een formule (onthoud de verticale maten || gemiddelde “determinant van”):
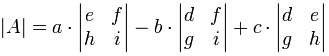
“de determinant van A is gelijk aan a maal de determinant van …,
Voor 4×4 Matrices en Hoger
Het patroon blijft voor 4×4 matrices:
- plus een keer de determinant van de matrix die is niet in een rij of kolom
- min b keer de determinant van de matrix die is niet in b rij of kolom
- plus c keer de determinant van de matrix die is niet in de c rij of kolom
- minus d maal de determinant van de matrix die is niet in d rij of kolom

Als een formule:
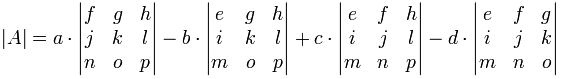
let op de +−+− patroon (+een.,.. – b… + c… – d…). Dit is belangrijk om te onthouden.
het patroon gaat verder voor 5 × 5 matrices en hoger. Meestal het beste om een Matrix Calculator te gebruiken voor die!
niet de enige manier
deze berekeningsmethode wordt de “Laplace-uitbreiding” genoemd en ik vind het leuk omdat het patroon Gemakkelijk te onthouden is. Maar er zijn andere methoden (zodat je het Weet).,
samenvatting
- voor een 2×2-matrix is de determinant ad – bc
- voor een 3×3-matrix vermenigvuldig a met de determinant van de 2×2-matrix die niet in de rij of kolom van a staat, ook voor b en c, maar onthoud dat b een negatief teken heeft!
- het patroon gaat verder voor grotere matrices: vermenigvuldig a met de determinant van de matrix die niet in A ‘ S rij of kolom staat, ga zo verder over de hele rij, maar denk aan het + − + − patroon.
Geef een reactie