Geluid Snelheid in Gassen

De snelheid van het geluid in een ideaal gas wordt gegeven door de relatie

Toon

• R = universele gasconstante = 8.314 J/mol K),
• T = de absolute temperatuur
• M = molecuulgewicht van het gas in kg/mol
• γ = de adiabatische constante, kenmerk van het specifieke gas

Voor de lucht, de adiabatische constante γ = 1.,4 en de gemiddelde molecuulmassa voor droge lucht is 28,95 gm / mol. Dit leidt tot

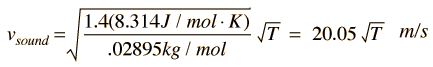
door deze berekening voor lucht bij 0°C geeft vsound = 331,39 m/s en bij 1°C geeft vsound = 332,00 m/s., Dit leidt tot een veelgebruikte benaderingsformule voor de geluidssnelheid in de lucht:

voor temperaturen bij kamertemperatuur kan de geluidssnelheid in de lucht worden berekend op basis van deze handige benaderende relatie, maar de meer algemene relatie is nodig voor berekeningen in helium of andere gassen.

de bovenstaande berekening werd gedaan voor droge lucht, en het vochtgehalte in de lucht zou naar verwachting de geluidssnelheid iets verhogen omdat het molecuulgewicht van waterdamp 18 is vergeleken met 28.,95 voor droge lucht. Een herzien gemiddelde molecuulgewicht kan worden berekend op basis van de dampdruk van water in de lucht. Echter, de aanname van een adiabatische constante van γ = 1.4 gebruikt in de berekening is gebaseerd op de diatomaire moleculen N2 en O2 en is niet van toepassing op watermoleculen. Dus de gedetailleerde modellering van het effect van waterdamp op de geluidssnelheid zou zich moeten vestigen op een geschikte waarde van γ te gebruiken.