|
twee driehoeken zijn congruent als ze:
maar we hoeven niet alle drie zijden en alle drie hoeken te kennen …meestal is drie van de zes genoeg. |
Er zijn vijf manieren om te vinden of twee driehoeken congruent zijn: SSS, SAS, ASA, AAS en HL.,
SSS (side, side, side)
SSS staat voor “side, side, side” en betekent dat we twee driehoeken hebben met alle drie zijden gelijk.
bijvoorbeeld:
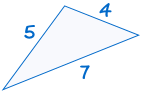 |
is congruent aan: | 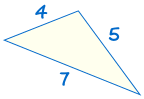 |
(Zie het Oplossen van SSS Driehoeken om meer te weten)
Als drie zijden van een driehoek gelijk zijn aan drie zijden van de andere driehoek, driehoeken zijn congruent.,
SAS (side, angle, side)
SAS staat voor “side, angle, side” en betekent dat we twee driehoeken hebben waarvan we weten dat twee zijden en de meegeleverde hoek gelijk zijn.,
bijvoorbeeld:
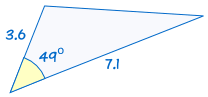 |
is congruent aan: | 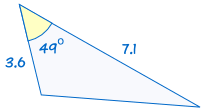 |
(Zie het Oplossen van SAS Driehoeken om meer te weten)
Als twee zijden en de hoek van een driehoek gelijk zijn aan de overeenkomstige zijden en de hoek van een andere driehoek, driehoeken zijn congruent.,
ASA (angle, side, angle)
ASA staat voor “angle, side, angle” en betekent dat we twee driehoeken hebben waarvan we weten dat twee hoeken en de meegeleverde zijde gelijk zijn.,
bijvoorbeeld:
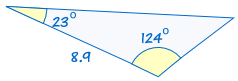 |
is congruent aan: | 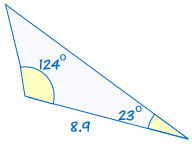 |
(Zie het Oplossen van ASA Driehoeken om meer te weten)
Als twee hoeken en zijden van een driehoek zijn gelijk aan de overeenkomstige hoeken en zijden van de andere driehoek, driehoeken zijn congruent.,
AAS (angle, angle, side)
AAS staat voor “angle, angle, side” en betekent dat we twee driehoeken hebben waarvan we weten dat twee hoeken en de niet-opgenomen zijde gelijk zijn.,
bijvoorbeeld:
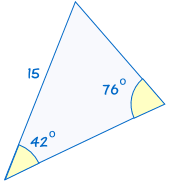 |
is congruent aan: | 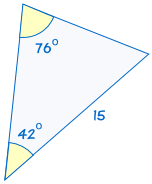 |
(Zie Problemen met de AAS Driehoeken om meer te weten)
Als twee hoeken en de niet-opgenomen zijde van een driehoek gelijk zijn aan de overeenkomstige hoeken en zijden van de andere driehoek, driehoeken zijn congruent.
HL (hypotenusa, been)
Dit geldt alleen voor rechthoekige driehoeken!,
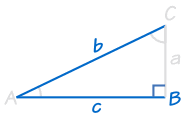 |
en | 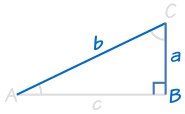 |
HL staat voor “schuine zijde, Been” (de langste zijde van een rechthoekige driehoek is de “schuine zijde”, de andere twee zijden worden genoemd “benen”)
Het betekent dat we twee rechthoekige driehoeken met
- dezelfde lengte van de schuine zijde en
- dezelfde lengte voor één van de andere twee poten.
Het maakt niet uit welk been aangezien de driehoeken kunnen worden geroteerd.,
bijvoorbeeld:
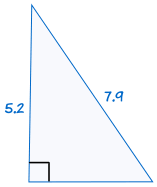 |
is congruent aan: | 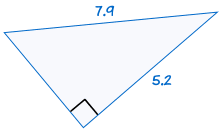 |
(Zie de Stelling van Pythagoras om meer te weten)
Als de schuine zijde en een poot van een rechthoekige driehoek zijn gelijk aan de corresponderende schuine zijde en been van een andere rechthoekige driehoek, de twee driehoeken zijn congruent.
voorzichtig! Gebruik ” AAA ”
AAA betekent dat we alle drie hoeken van een driehoek krijgen, maar geen zijden.,
Dit is niet genoeg informatie om te beslissen of twee driehoeken congruent zijn!
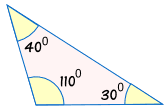
omdat de driehoeken dezelfde hoeken kunnen hebben, maar verschillende groottes kunnen hebben:
| is niet congruent aan: | 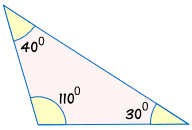 |
zonder ten minste één zijde te weten, weten we niet zeker of twee driehoeken congruent zijn.





Geef een reactie