in deze les gaan we de vijf (5) common logische connectives of operators construeren. Ze worden beschouwd als gemeenschappelijke logische connectiva omdat ze erg populair, nuttig en altijd samen onderwezen.
voordat we beginnen, stel ik voor dat u mijn andere les bekijkt waarin de link hieronder wordt getoond.
deze inleidende les over waarheidstabellen bevat voorkennis of informatie die u zal helpen de inhoud van deze les beter te begrijpen.,
Inleiding tot waarheidstabellen, Statements en Connectiva
Le ‘ s beginnen met een opsomming van de vijf (5) gemeenschappelijke logische connectiva.
de vijf (5) gemeenschappelijke logische Connectiva of operatoren
- logische negatie
- logische conjunctie (en)
- logische disjunctie (inclusief OR)
- logische implicatie (voorwaardelijk)
- logische Biconditionele (Dubbele implicatie)
I., Waarheidstabel van logische negatie
de negatie van een verklaring is ook een verklaring met een waarheidswaarde die precies tegengesteld is aan die van de oorspronkelijke verklaring. Bijvoorbeeld, de negatie van het statement wordt symbolisch geschreven als
~\large{P} of \large{\neg P}.
~{p} of {\neg P} wordt gelezen als”not P.”
onthoud: de negatie-operator die wordt aangeduid met het symbool ~ of \neg neemt de waarheidswaarde van het oorspronkelijke statement en voert dan het exacte tegenovergestelde van de waarheidswaarde uit., Met andere woorden, ontkenning keert gewoon de waarheidswaarde van een bepaalde verklaring om. Dus, als verklaring P waar is, dan is de waarheidswaarde van haar negatie vals. Op dezelfde manier als P vals is, is de waarheidswaarde van haar negatie waar.

II. waarheidstabel van logische Conjunctie
een conjunctie is een type samengestelde statement dat bestaat uit twee proposities (ook bekend als eenvoudige statements) die worden samengevoegd door de en-operator.,
Het symbool dat wordt gebruikt om de en of logische conjunctie operator weer te geven is \color{red}\Large{\wedge}. Het lijkt op een omgekeerde letter V.
als we twee eenvoudige statements P en Q hebben, en we willen een samengestelde statement vormen samen met de en operator, kunnen we het schrijven als:
\large{P \wedge Q}.
{p \wedge Q} wordt gelezen als”P en Q.”
onthoud: de waarheidswaarde van het samengestelde statement P \wedge Q is alleen waar als de waarheidswaarden P en Q beide waar zijn., Anders is P \ wig Q onwaar.
merk in de waarheidstabel hieronder op dat wanneer P waar is en Q Waar, P \wedge Q Waar is. De andere drie combinaties van stellingen P en Q zijn echter onwaar.

III. waarheidstabel van logische disjunctie
een disjunctie is een soort samengestelde statement dat bestaat uit twee eenvoudige statements gevormd door de statements te verbinden met de OR operator.
in een disjunctie statement is het gebruik van OR inclusief. Dat betekent “het een of het ander” of beide.,
Het symbool dat wordt gebruikt om de OR of logische disjunctie operator weer te geven is \color{red}\Large{ \vee }. Het lijkt op de letter V van het alfabet.
twee proposities P en Q die door of operator worden samengevoegd om een samengestelde verklaring te vormen, worden geschreven als:
\large{P \vee Q}.
{p \vee Q} wordt gelezen als”P of Q.”
onthoud: de waarheidswaarde van het samengestelde statement P \vee Q is waar als de waarheidswaarde van beide eenvoudige statements P en Q Waar is., Moreso, P \ vee Q is ook waar wanneer de waarheidswaarden van beide stellingen P en Q Waar zijn. Echter, de enige keer dat de disjunctie statement P \vee Q onwaar is, gebeurt wanneer de waarheidswaarden van zowel P als Q onwaar zijn.
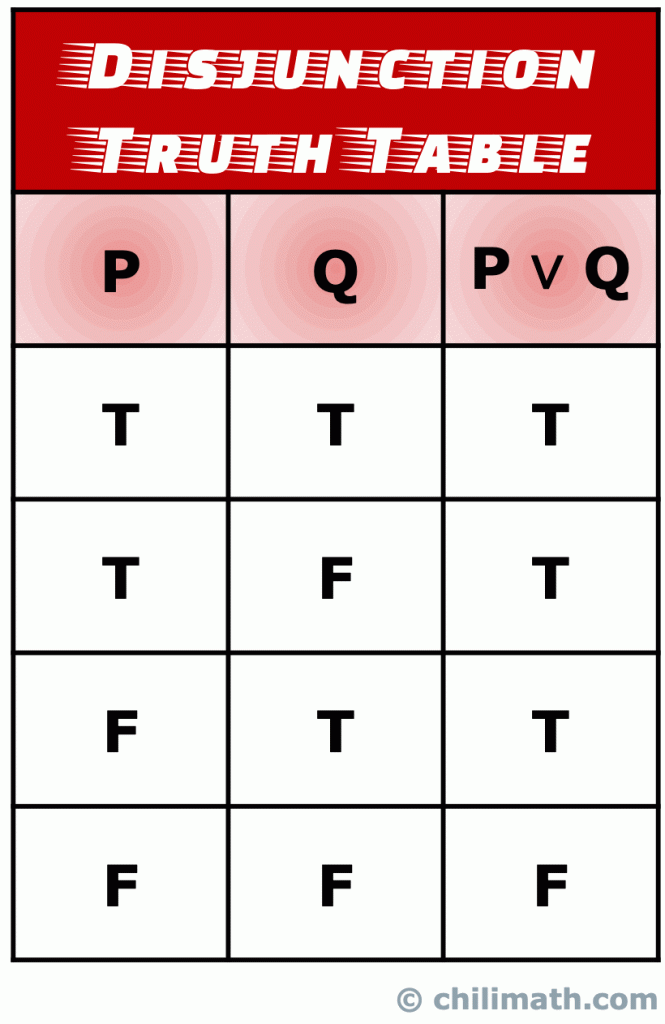
IV. waarheidstabel van logische implicatie
een implicatie (ook bekend als een voorwaardelijke verklaring) is een type samengestelde verklaring die wordt gevormd door twee eenvoudige statements te verbinden met de logische implicatie connective or operator.,
Het symbool dat wordt gebruikt om de logische implicatie-operator weer te geven is een pijl die naar rechts wijst, dus een pijl naar rechts.

wanneer twee eenvoudige statements P en Q worden samengevoegd door de implicatie operator, hebben we:
\large{P \to Q}.
- waar P bekend staat als de hypothese
- waar Q bekend staat als de conclusie
Er zijn vele manieren om de voorwaardelijke {P \to Q} te lezen., Hieronder staan enkele van de weinige veel voorkomende.
onthoud: de waarheidswaarde van het samengestelde statement P \tot en met Q is waar wanneer zowel de eenvoudige statements P als Q Waar zijn. Moreso, P \tot Q is altijd waar als P onwaar is. Het enige scenario dat P \tot Q onwaar is gebeurt als P waar is, en Q onwaar is.
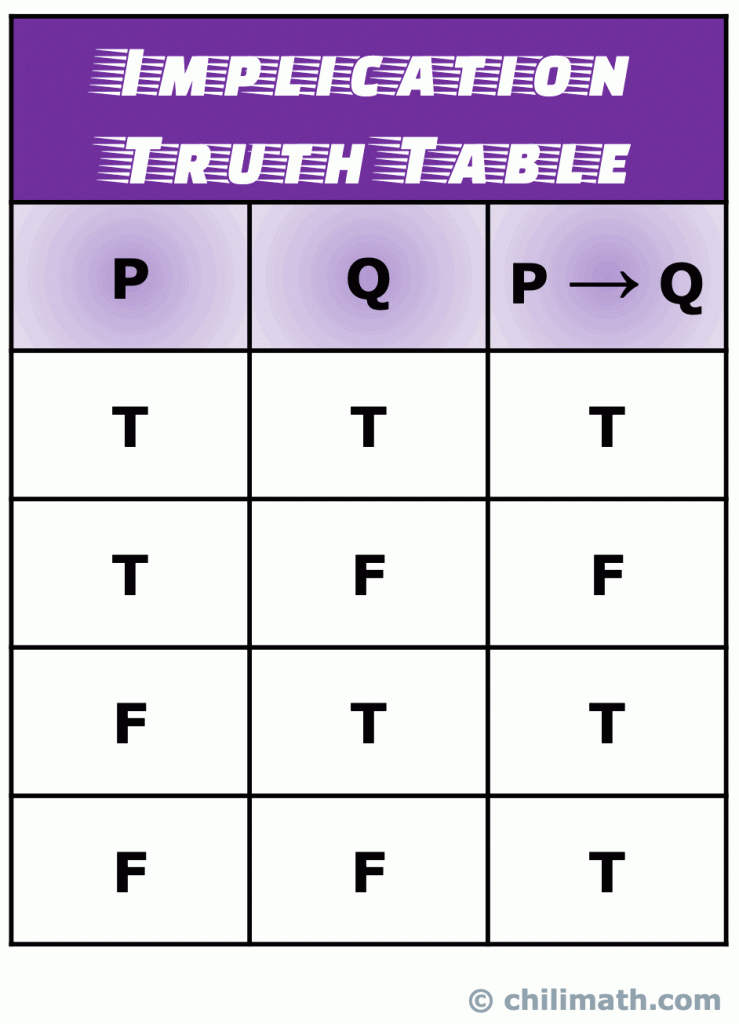
V., Een dubbele implicatie (ook bekend als een biconditionele verklaring) is een soort samengestelde verklaring die wordt gevormd door het verbinden van twee eenvoudige verklaringen met de biconditionele operator. Een dubbelzijdige verklaring is eigenlijk een combinatie van een voorwaardelijke verklaring en het omgekeerde ervan.
de tweezijdige operator wordt aangeduid met een tweekoppige pijl.,

Wanneer u deelneemt aan twee eenvoudige stellingen (ook bekend als moleculair verklaringen) met de biconditional operator, krijgen we:
\Large{P \leftrightarrow Q}
{P \leftrightarrow Q} is te lezen als “P als en slechts als Q.,”
- waar P bekend staat als de antecedent
- waar Q bekend staat als de consequente
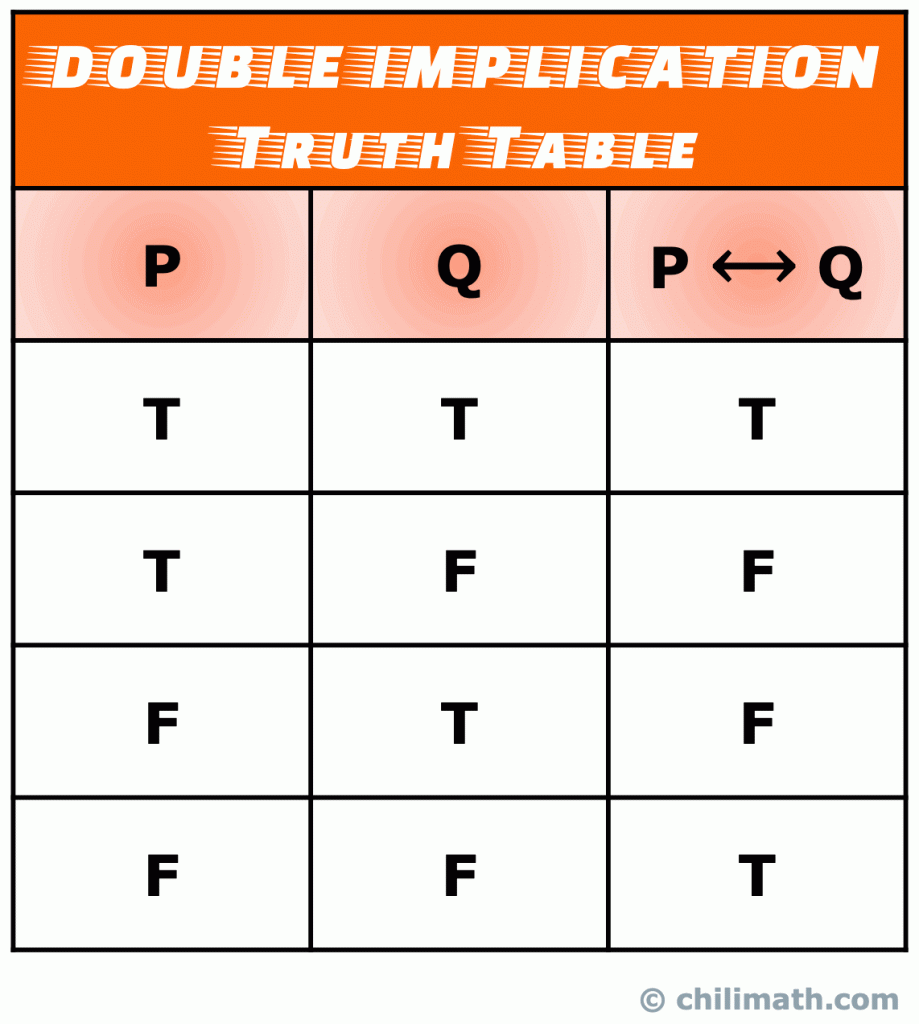
onthoud: de waarheidswaarde van de tweezijdige statement P \leftrightarrow Q is waar wanneer beide eenvoudige statements P en Q beide waar of beide onwaar zijn. Anders is P \ Left rightarrow Q onwaar.
u bent wellicht ook geïnteresseerd in:
Inleiding tot waarheidstabellen, Statements en logische Connectives
Converse, Inverse, and Contrapositive of a Conditional Statement
Geef een reactie