|
dwa trójkąty są przystające, jeśli mają:
ale nie musimy znać wszystkich trzech stron i wszystkich trzech kątów …zazwyczaj trzy z sześciu wystarczy. |
Istnieje pięć sposobów, aby znaleźć, czy dwa trójkąty są przystające: SSS, SAS, ASA, AAS i HL.,
SSS (side, side, side)
SSS oznacza „side, side, side” i oznacza, że mamy dwa trójkąty o wszystkich trzech bokach równych.
na przykład:
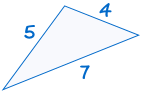 |
jest zgodne z: | 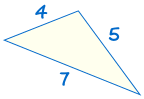 td td |
(zobacz Rozwiązywanie trójkątów SSS, aby dowiedzieć się więcej)
Jeśli trzy boki jednego trójkąta są równe trzem bokom innego trójkąta, Trójkąty są przystające.,
SAS (side, angle, side)
SAS oznacza „side, angle, side” i oznacza, że mamy dwa trójkąty, w których wiemy, że dwa boki i kąt są równe.,
na przykład:
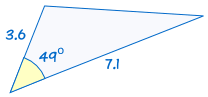 |
jest zgodne z: | 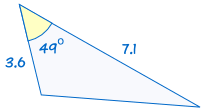 |
(zobacz Rozwiązywanie trójkątów SAS, aby dowiedzieć się więcej)
jeśli dwa boki i uwzględniony kąt jednego trójkąta są równe odpowiednim bokom i kątowi innego trójkąta, trójkąty są przystające.,
Asa (angle, side, angle)
Asa oznacza „kąt, bok, kąt” i oznacza, że mamy dwa trójkąty, w których znamy dwa kąty, a dołączona strona jest równa.,
na przykład:
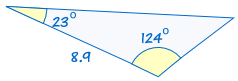 |
jest zgodne z: | 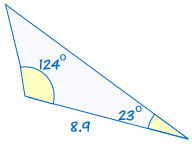 |
(zobacz Rozwiązywanie trójkątów asa, aby dowiedzieć się więcej)
jeśli dwa kąty i dołączony bok jednego trójkąta są równe odpowiednim kątom i boku innego trójkąta, trójkąty są przystające.,
AAS (angle, angle, side)
AAS oznacza „kąt, kąt, bok” i oznacza, że mamy dwa trójkąty, w których znamy dwa kąty i nieuwzględnione strony są sobie równe.,
na przykład:
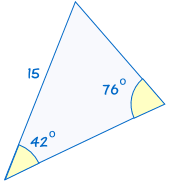 |
jest zgodne z: | 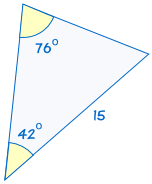 |
(zobacz Rozwiązywanie trójkątów AAS, aby dowiedzieć się więcej)
jeśli dwa kąty i nieuwzględniona strona jednego trójkąta są równe odpowiednim kątom i stronie innego trójkąta, Trójkąty są przystające.
HL (przeciwprostokątna, noga)
ten dotyczy tylko trójkątów kątowych!,
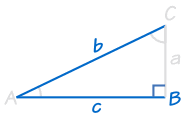 |
hl oznacza „przeciwprostokątna, noga” (najdłuższy bok trójkąta prostokątnego nazywa się „przeciwprostokątną”, pozostałe dwa boki nazywane są „nogami”)
oznacza to, że mamy dwa trójkąty prostokątne o
- tej samej długości przeciwprostokątnej i
- tej samej długości dla jednej z pozostałych dwóch nóg.
nie ma znaczenia, która noga, ponieważ Trójkąty mogą być obracane.,
na przykład:
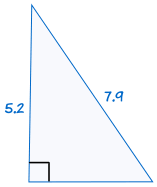 |
jest zgodne z: | 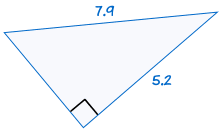 |
(zobacz twierdzenie Pitagorasa, aby dowiedzieć się więcej)
Jeśli przeciwprostokątna i jedna noga jednego trójkąta kątowego są równe odpowiadającej przeciwprostokątnej i nogi innego trójkąta kątowego, dwa trójkąty są przystające.
Uwaga! Nie używaj „AAA”
AAA oznacza, że mamy wszystkie trzy kąty trójkąta, ale nie ma boków.,
to za mało informacji, aby zdecydować, czy dwa trójkąty są zgodne!
ponieważ Trójkąty mogą mieć te same kąty, ale mają różne rozmiary:
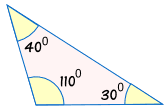 |
nie jest zgodny z: |  |
nie znając przynajmniej jednej strony, nie możemy być pewni, czy dwa trójkąty są zbieżne.





Dodaj komentarz