ciśnienie i KMT
makroskopowe zjawiska ciśnienia można wyjaśnić w kategoriach kinetycznej molekularnej teorii gazów. Załóżmy przypadek, w którym cząsteczka gazu (reprezentowana przez kulę) znajduje się w polu o długości L (Rys. 1). Korzystając z założeń przedstawionych powyżej i biorąc pod uwagę, że kula porusza się tylko w kierunku x, możemy zbadać instancję kuli zderzającej się elastycznie z jedną ze ścian pudełka.,
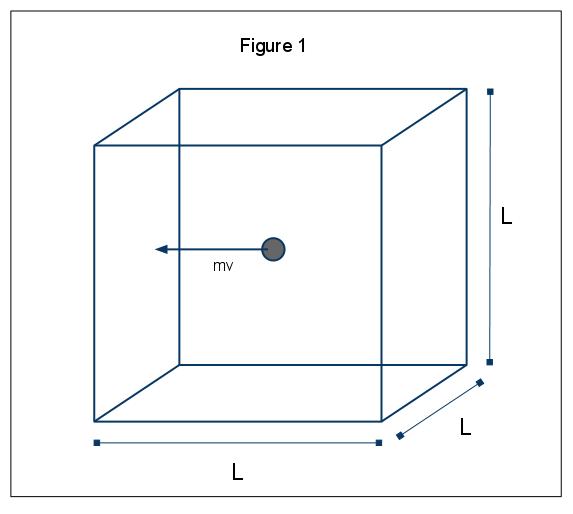
moment P=MV, w tym przypadku p=mvx, ponieważ rozważamy tylko wymiar x. Całkowita zmiana pędu dla tej kolizji jest następnie podana przez
\
biorąc pod uwagę, że czas potrzebny między zderzeniami cząsteczki ze ścianą wynosi L/vx, możemy podać częstotliwość zderzeń cząsteczki z daną ścianą Pudełka na jednostkę czasu jako vx/2L., Można teraz rozwiązać dla zmiany pędu na jednostkę czasu:
\
rozwiązanie dla pędu na jednostkę czasu daje siłę wywieraną przez obiekt (F=ma=p / czas)., Z wyrażeniem, które f=mvx2/L można teraz rozwiązać dla ciśnienia wywieranego przez zderzenie molekularne, gdzie obszar jest podany jako obszar jednej ściany pudełka, A=L2:
\
\
wyrażenie można teraz zapisać w kategoriach ciśnienia związanego ze zderzeniami z N liczby cząsteczek:
\
wyrażenie to można teraz dostosować do ruchu w kierunkach x, y i z za pomocą średniej kwadratowej prędkość dla trzech wymiarów i duża wartość n., Wyrażenie jest teraz zapisywane jako:
\
to wyrażenie daje teraz ciśnienie, makroskopową jakość, w kategoriach ruchu atomowego. Znaczenie powyższej zależności polega na tym, że ciśnienie jest proporcjonalne do średniej-kwadratowej prędkości cząsteczek w danym pojemniku. W związku z tym, wraz ze wzrostem prędkości cząsteczkowej, wzrasta ciśnienie wywierane na pojemnik.
Dodaj komentarz