reklamy:
znajomość pojęcia linii budżetowej lub tego, co jest również nazywane ograniczeniem budżetowym, jest niezbędna do zrozumienia teorii równowagi konsumenta.
wyższa krzywa obojętności pokazuje wyższy poziom satysfakcji niż niższy. Dlatego konsument, starając się zmaksymalizować swoją satysfakcję, będzie starał się osiągnąć jak najwyższą krzywą obojętności.,
ale w dążeniu do kupowania coraz większej ilości towarów, a tym samym uzyskania coraz większej satysfakcji, musi pracować pod dwoma ograniczeniami: po pierwsze, musi płacić ceny za towary, a po drugie, ma ograniczony dochód pieniężny, z którego można go kupić. Tak więc, jak daleko posunąłby się za swoje zakupy, zależy od cen towarów i dochodów pieniężnych, które musi wydać na towary.,
ADVERTISEMENTS:
w celu wyjaśnienia równowagi konsumenta istnieje również potrzeba wprowadzenia do analizy krzywej obojętności linii budżetowej, która przedstawia ceny towarów i dochody pieniężne konsumenta.
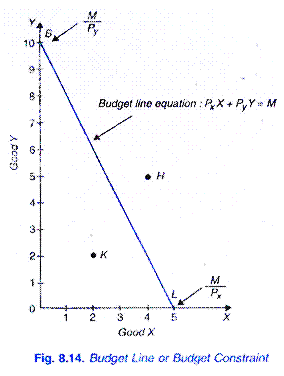
50 wydać na dwa towary X i Y. niech cena dobra X na rynku będzie Rs. 10 na jednostkę i Y Rs. 5 za sztukę. Jeśli konsument wydaje cały swój dochód Rs. 50 na dobre X, kupi 5 jednostek X; jeśli wyda cały dochód z Rs., 50 na dobrym Y kupiłby 10 jednostek Y. Jeśli narysuje się linię prostą łączącą 5x i 10Vis, otrzymamy to, co nazywa się linią cenową lub linią budżetową.
tak więc linia budżetowa pokazuje wszystkie te kombinacje dwóch towarów, które konsument może kupić wydając dany dochód pieniężny na dwa towary po podanych cenach. Spojrzenie na Rys. 8.14 pokazuje, że z Rs. 50, a ceny X i Y wynoszą 10 i Rs. 5 odpowiednio konsument może kupić l0Y i OX, lub stoisko IX; lub 6Y i 2x, lub 4y i 3x itp.,
reklama:
innymi słowy, może kupić dowolną kombinację, która leży w linii budżetowej z jego podanym dochodem pieniężnym i podanymi cenami towarów. Należy dokładnie zauważyć, że jakakolwiek kombinacja tych dwóch towarów, takich jak H (5Y i 4X), która leży powyżej i poza daną linią budżetową, będzie poza zasięgiem konsumenta.
ale jakakolwiek kombinacja leżąca w linii budżetowej np. K (2x i 2Y) będzie dobrze w zasięgu konsumenta, ale jeśli kupi taką kombinację, NIE WYDA całego swojego dochodu Rs. 50., Tak więc, przy założeniu, że całość danego dochodu jest wydawana na dane towary i po określonych ich cenach, konsument musi wybierać spośród wszystkich tych kombinacji, które leżą w linii budżetowej.
z góry widać, że linia budżetowa graficznie pokazuje ograniczenie budżetowe. Kombinacje towarów leżących po prawej stronie linii budżetowej są nieosiągalne, ponieważ dochód konsumenta nie jest wystarczający do zakupu tych kombinacji., Biorąc pod uwagę dochody konsumenta i ceny obu towarów, połączenia towarów leżących po lewej stronie linii budżetowej są osiągalne, to znaczy konsument może kupić dowolny z nich.
ważne jest również, aby pamiętać, że przechwytywanie OB na osi Y na Rys. 8.14 równa się kwota jego całego dochodu (M) podzielona przez cenę (PY) towaru Y. czyli OB = m/PY. Podobnie, przechwytywanie OL na osi X mierzy całkowity dochód podzielony przez cenę towaru X. Tak więc OL = M / Px.,
reklamy:
linia budżetowa może być zapisana algebraicznie w następujący sposób:

gdzie Px i Py oznaczają odpowiednio ceny towarów X i Y, A M oznacza dochód pieniężny:
powyższa linia budżetowa równanie (1) zakłada, że biorąc pod uwagę dochód pieniężny konsumenta i ceny obu towarów, każda kombinacja leżąca w linii budżetowej będzie kosztować tę samą kwotę pieniędzy i dlatego może być zakupiona z danym dochodem., Linię budżetową można zdefiniować jako zbiór kombinacji dwóch towarów, które można nabyć, jeśli całość danego dochodu zostanie na nie wydatkowana, a jej nachylenie jest równe ujemnemu stosunkowi cenowemu.
przestrzeń Budżetowa:
należy dokładnie zrozumieć, że równanie budżetu PxX + PyY= m lub Y = M/Py – Px / PyX przedstawione przez linię budżetową na Rys. 8.14 opisuje jedynie linię budżetową, a nie przestrzeń budżetową., Przestrzeń budżetowa pokazuje zbiór wszystkich kombinacji dwóch towarów, które można kupić wydając całość lub część danego dochodu.
innymi słowy, przestrzeń budżetowa reprezentuje szansę ustawioną dla konsumenta, czyli wszystkie te kombinacje dwóch towarów, które może kupić, biorąc pod uwagę jego ograniczenia budżetowe. Tak więc przestrzeń budżetowa oznacza zbiór wszystkich kombinacji dwóch dóbr, dla których dochód wydany na dobro X (tj. PxX i dochód wydany na dobro Y (tj. PyY) nie może przekraczać danego dochodu pieniężnego.,
dlatego możemy algebraicznie wyrazić przestrzeń budżetową w następującej postaci nierówności:
PXX + PyY < m, lub m > PxX + PyY
reklamy:
przestrzeń budżetowa została pokazana graficznie na rys. 8.15 jako zacieniony obszar. Przestrzeń budżetowa to cały obszar objęty Linią budżetową BL i obie osie.
zmiany cen i zmiany w linii budżetowej:
teraz, co się stanie z linią budżetową, jeśli zmienią się ceny towarów lub zmiany dochodów., Weźmy najpierw przypadek zmian cen towarów. Ilustruje to rys. 8.16. Załóżmy, że linia budżetowa na początku jest BL, biorąc pod uwagę pewne ceny towarów X i Y oraz pewien dochód. Załóżmy, że cena x spada, cena Y i dochód pozostają bez zmian. Teraz, przy niższej cenie X konsument będzie mógł kupić więcej ilości X niż wcześniej z jego danym dochodem.
niech po niższej cenie X dany dochód kupuje OL' Z X, który jest większy niż OL., Ponieważ cena Y pozostaje taka sama, nie może nastąpić zmiana ilości zakupionego towaru Y z tym samym dochodem, a w rezultacie nie nastąpi zmiana punktu B. Tak więc, wraz ze spadkiem ceny towaru X, dochodem pieniężnym konsumenta i ceną Y pozostającą na stałym poziomie, linia budżetowa przesunie się na prawo do nowej pozycji BL”.,
reklamy:
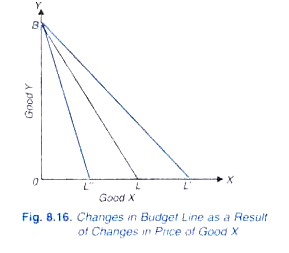
co się stanie z linią budżetową (początkowa linia budżetowa BL), jeśli cena dobra x wzrośnie, Cena dobre y i dochody pozostały niezmienione. Przy wyższej cenie Dobra X konsument może kupić mniejszą ilość X, powiedzmy OL ” niż wcześniej. Tak więc, wraz ze wzrostem ceny X linia budżetowa przesunie się w lewo do nowej pozycji BL”.
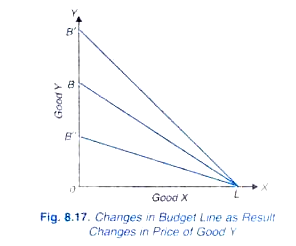
Rysunek 8.,17 pokazuje zmiany w linii budżetowej, gdy cena dobra Y spada lub wzrasta, przy czym cena X i dochód pozostają takie same. W tym początkowa linia budżetowa to BL. Przy spadku ceny dobra Y, pozostałe rzeczy pozostające bez zmian, konsument może kupić więcej Y z danym dochodem pieniężnym, a zatem linia budżetowa przesunie się powyżej do LB”. Podobnie, wraz ze wzrostem ceny Y, inne rzeczy są stałe, linia budżetowa przesunie się poniżej do LB”.,
reklamy:
zmiany w dochodach i zmiany w linii budżetowej:
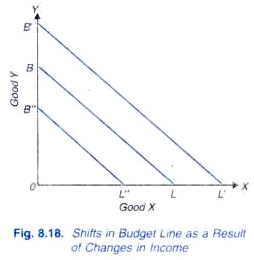
teraz pytanie brzmi, co stanie się z linią budżetową, jeśli dochody ulegną zmianie, podczas gdy ceny towarów pozostają takie same. Wpływ zmian w dochodach na linię budżetową przedstawiono na Rys. 8.18. Niech BL będzie początkową linią budżetową, biorąc pod uwagę pewne ceny towarów i dochodów. Jeśli dochód konsumenta wzrasta, a ceny towarów X i y pozostają niezmienione, linia cenowa przesuwa się w górę (powiedzmy do BL') i jest równoległa do pierwotnej linii budżetowej BL.,
dzieje się tak dlatego, że przy zwiększonym dochodzie konsument jest w stanie kupić proporcjonalnie większą ilość dobra X niż wcześniej, jeśli całość dochodu jest wydawana na X, i proporcjonalnie większą ilość dobra Y niż wcześniej, jeśli całość dochodu jest wydawana na Y. z drugiej strony, jeśli dochód konsumenta spada, ceny obu towarów X i Y pozostają bez zmian, linia budżetowa przesuwa się w dół (powiedzmy, do B”L”), ale pozostaje równoległa do pierwotnej linii cenowej BL.,
dzieje się tak dlatego, że niższy dochód kupi proporcjonalnie mniejszą ilość dobra X, jeśli cały dochód zostanie wydany na X, i proporcjonalnie mniejszą ilość dobra Y, jeśli cały dochód zostanie wydany na Y.
z góry jasne jest, że linia budżetowa ulegnie zmianie, jeśli zmienią się ceny towarów lub zmieni się dochód konsumenta.
reklamy:
zatem dwoma wyznacznikami linii budżetowej są:
(a) ceny towarów i
(b) dochód konsumenta przeznaczony na towary.,
nachylenie linii budżetowej i ceny dwóch towarów:
ważne jest również, aby pamiętać, że nachylenie linii budżetowej jest równe stosunkowi cen dwóch towarów. Można to udowodnić za pomocą rys. 8.14. Załóżmy, że dany dochód konsumenta jest M, A podane ceny towarów X i Y są odpowiednio Px i Py.
nachylenie linii budżetowej BL wynosi OB/OL. Zamierzamy udowodnić, że nachylenie to jest równe stosunkowi cen towarów X i Y.,
reklamy:
ilość zakupionego towaru X, jeżeli całość danego dochodu M jest na niego wydawana to OL. Dlatego ol x Px = m
ol = M/Px
obecnie ilość zakupionego dobra Y, jeśli całość danego dochodu M jest na niego wydawana, wynosi OB.

w ten sposób udowodniono, że nachylenie linii budżetowej BL jest równe stosunkowi cen dwóch towarów.
Dodaj komentarz