|
„Bi” oznacza „dwa” (podobnie jak rower ma dwa koła) … |
 |

rzucanie monetą:
- czy otrzymaliśmy orły (H) lub
- reszka (t)
mówimy, że prawdopodobieństwo lądowania monety h wynosi ½
, a prawdopodobieństwo lądowania monety t wynosi ½
rzućmy monetą!
Rzuć uczciwą monetą trzy razy … jaka jest szansa na zdobycie dwóch głów?,tr>












Which outcomes do we want?,
„dwie głowy” mogą być w dowolnej kolejności: „HHT”, ” THH ” i ” HTH ” wszystkie mają dwie głowy (i jeden ogon).
tak więc 3 z wyników daje „dwie głowy”.
jakie jest prawdopodobieństwo każdego wyniku?,ations are(P oznacza „prawdopodobieństwo”):
- P(Trzy Głowy) = p(HHH) = 1/8
- p(dwie głowy) = P (HHT) + P (HTH) + P(THH) = 1/8 + 1/8 + 1/8 = 3/8
- P (jedna głowa) = P (HTT) + P (THT) + P (TTH) = 1/8 + 1/8 + 1/8 = 3/8
- P(Zero Heads) = p(TTT) = 1/8
możemy to zapisać w postaci zmiennej losowej, X, = „liczba głowic z 3 rzutów monety”:
- P(X = 3) = 1/8
- P(x = 2) = 3/8
- P(X = 1) = 3/8
- P(X = 0) = 1/8
i tak wygląda wykres:
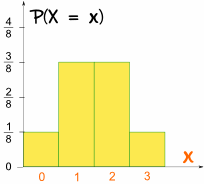
jest symetryczny!,
Tworzenie Formuły
teraz wyobraź sobie, że chcemy mieć szanse na 5 głów w 9 rzutach: lista wszystkich 512 wyników zajmie dużo czasu!
więc zróbmy wzór.
w naszym poprzednim przykładzie, jak możemy uzyskać wartości 1, 3, 3 i 1 ?
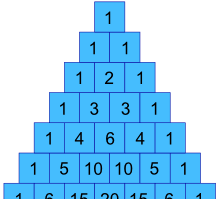
Cóż, rzeczywiście są w trójkącie Pascala !
Czy możemy zrobić je za pomocą formuły?
oczywiście, że możemy, i oto jest:
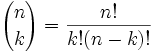
często nazywa się to „N wybierz k”
- n = całkowita liczba
- K = Liczba chcemy
- the „!,”oznacza ” czynnościowy”, np. 4! = 1×2×3×4 = 24
więcej na ten temat można przeczytać w zakładce kombinacje i permutacje.
spróbujmy:
wykorzystajmy go do trudniejszego Pytania:
do tej pory szanse na sukces lub porażkę były równie prawdopodobne.
ale co jeśli monety są stronnicze (lądują więcej na jednej stronie niż na drugiej) lub wybory nie są 50/50.
przykład: sprzedajesz kanapki. 70% ludzi wybiera kurczaka, reszta wybiera coś innego.
To jest tak jak w przykładzie Orzeł i reszka, ale z 70/30 zamiast 50/50.,
narysujmy diagram drzewa:

podświetlone są przypadki „dwóch kurczaków”.
Prawdopodobieństwo dla „dwóch kurczaków” wynosi 0,147, ponieważ mnożemy dwa 0,7 s i jeden 0,3 w każdym przypadku. Innymi słowy
0.147 = 0.7 × 0.7 × 0.3
lub, używając wykładników:
= 0.72 × 0.31
0.7 jest prawdopodobieństwem każdego wyboru, nazwijmy go p
2 jest liczbą wyborów, nazwijmy go k
i mamy (do tej pory):
= PK × 0.31
0.,3 jest prawdopodobieństwem przeciwnego wyboru, więc jest to: 1−p
1 jest liczbą przeciwnych wyborów, więc jest to: n−k
co daje nam:
= pk(1-p)(n-k)
gdzie
- p jest prawdopodobieństwem każdego wyboru, którego chcemy
- k jest liczbą wyborów, których chcemy
- n jest całkowitą liczbą wyborów, które chcemy wybór
teraz wiemy, że prawdopodobieństwo każdego wyniku wynosi 0,147
ok. To było dużo pracy dla czegoś, co już wiedzieliśmy, ale teraz mamy formułę, którą możemy użyć do trudniejszych pytań.,
teraz wiemy jak obliczyć ile:
n!k!(n-k)!
i prawdopodobieństwo każdego:
pk(1-p)(n-k)
po pomnożeniu razem otrzymujemy:
prawdopodobieństwo k Z N sposobów:
p(k Z n) = N!k!(n-k)! pk(1-p) (n-k)
ogólny Dwumianowy wzór prawdopodobieństwa
Ważne uwagi:
- próby są niezależne,
- istnieją tylko dwa możliwe wyniki w każdym badaniu,
- prawdopodobieństwo „sukcesu” w każdym badaniu jest stałe.,
Quincunx

pobaw się z Quincunx (przeczytaj Wyjaśnienie Quincunx), aby zobaczyć rozkład dwumianowy w akcji.
Rzuć matrycę
sprawiedliwa matryca jest wyrzucana cztery razy. Oblicz prawdopodobieństwo uzyskania:
- 0 dwójek
- 1 dwójek
- 2 dwójek
- 3 dwójek
- 4 dwójek
w tym przypadku N=4, p = P(Dwa) = 1/6
X jest zmienną losową „Liczba dwójek z czterech rzutów”.,
Zastąp x = 0 do 4 we wzorze:
P(k Z n) = N!k!(n-k)! pk(1-p) (n-k)
tak (do 4 miejsc po przecinku):
tym razem Wykres nie jest symetryczny:
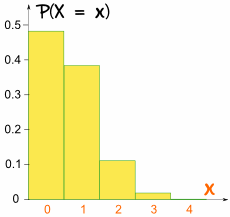
nie jest symetryczny!
jest przekrzywiony, ponieważ p nie jest 0.5

rowery sportowe
Twoja firma produkuje rowery sportowe. 90% przechodzi kontrolę końcową(a 10% nie powiedzie się i musi zostać naprawione).
Jaka jest oczekiwana średnia i zmienność 4 kolejnych kontroli?
najpierw obliczmy wszystkie prawdopodobieństwa.,
- n = 4,
- p = p (Pass) = 0.9
X jest zmienną losową „Liczba przejść z czterech kontroli”.
Zastąp x = 0 do 4 we wzorze:
P(k Z n) = N!k!(n-k)! pk (1-p)(n-k)
Średnia, wariancja i odchylenie standardowe
obliczmy średnią, wariancję i odchylenie standardowe dla rowerów sportowych.
istnieją dla nich (względnie) proste formuły. Są trochę trudne do udowodnienia,ale działają!,
średnia lub” wartość oczekiwana ” wynosi:
μ = np
wzór wariancji wynosi:
wariancja: σ2 = np(1-p)
a odchylenie standardowe to pierwiastek kwadratowy wariancji:
σ = √(np(1-p))
dla rowerów sportowych:
wariancja: σ2= 4 × 0.9 × 0.1 = 0.36
odchylenie standardowe wynosi:
σ = √(0.36) = 0.6

Dodaj komentarz