Statystyka bayesowska wyjaśniona początkującym w prostym języku angielskim

przegląd

• wady statystyk częstościowych prowadzą do potrzeby statystyk bayesowskich
• Odkryj statystykę Bayesowską i wnioskowanie bayesowskie
• istnieją różne metody testowania znaczenia modelu, takie jak wartość p, przedział ufności itp

wprowadzenie

bayesowskie statystyki nadal pozostają niezrozumiałe w umysłach wielu analityków., Będąc zdumieni niesamowitą mocą uczenia maszynowego, wielu z nas stało się niewiernymi statystykom. Skupiamy się na badaniu uczenia maszynowego. Czy to nie prawda?

nie rozumiemy, że uczenie maszynowe nie jest jedynym sposobem rozwiązywania rzeczywistych problemów. W kilku sytuacjach nie pomaga nam to rozwiązywać problemów biznesowych, mimo że problemy te są związane z danymi. Mówiąc co najmniej, znajomość statystyk pozwoli Ci pracować nad złożonymi problemami analitycznymi, niezależnie od wielkości danych.,

w 1770 roku Thomas Bayes wprowadził „twierdzenie Bayesa”. Nawet po stuleciach znaczenie „statystyk bayesowskich” nie zanikło. W rzeczywistości, dziś Temat ten jest nauczany w ogromnej głębi w niektórych z wiodących uniwersytetów na świecie.

z tym pomysłem stworzyłem ten poradnik dla początkujących na temat statystyk bayesowskich. Próbowałem wyjaśnić pojęcia w sposób uproszczony za pomocą przykładów. Pożądana jest wcześniejsza znajomość podstawowego prawdopodobieństwa & statystyki., Powinieneś sprawdzić ten kurs, aby uzyskać wyczerpujący niski poziom statystyk i prawdopodobieństwa.

pod koniec tego artykułu będziesz miał konkretne zrozumienie statystyk bayesowskich i powiązanych z nimi pojęć.,>Twierdzenie Bayesa

wnioskowanie bayesowskie

• funkcja prawdopodobieństwa Bernoulliego
• rozkład wcześniejszych przekonań
• rozkład tylnych przekonań

Test istotności – częstotliwości vs Bayesowski

• wartość p
• przedziały ufności
• Współczynnik Bayesa
• przedział wysokiej gęstości (HDI)

li>

zanim zagłębimy się w statystykę bayesowską, poświęćmy kilka minut na zrozumienie statystyk częstych, bardziej popularnej wersji statystyk, z którą większość z nas się spotyka i nieodłącznych w tym problemów.,

statystyki Frequentist

debata między frequentist i bayessian prześladuje początkujących od wieków. Dlatego ważne jest, aby zrozumieć różnicę między tymi dwoma i jak istnieje cienka linia rozgraniczenia!

jest to najczęściej stosowana technika wnioskowania w świecie statystycznym. W rzeczywistości, ogólnie jest to pierwsza szkoła myślenia, że osoba wchodząca w świat statystyk spotyka.

Statystyka Częstościowa sprawdza, czy zdarzenie (hipoteza) występuje, czy nie., Oblicza prawdopodobieństwo zdarzenia w długim okresie eksperymentu (tzn. eksperyment powtarza się w tych samych warunkach, aby uzyskać wynik).

tutaj pobierane są rozkłady próbkowania o stałej wielkości. Następnie eksperyment jest teoretycznie powtarzany nieskończoną liczbę razy, ale praktycznie odbywa się z zamiarem zatrzymania. Na przykład, przeprowadzam eksperyment z zamiarem zatrzymania w umyśle, że zatrzymam eksperyment, gdy zostanie powtórzony 1000 razy lub zobaczę minimum 300 głów w rzucie monetą.

wejdźmy teraz głębiej.,

teraz zrozumiemy statystyki na przykładzie rzutu monetą. Celem jest oszacowanie uczciwości monety. Poniżej znajduje się tabela przedstawiająca częstotliwość Orłów:

wiemy, że prawdopodobieństwo zdobycia głowy po wrzuceniu uczciwej monety wynosi 0.5. No. of heads przedstawia rzeczywistą liczbę uzyskanych głowic. Difference jest różnica pomiędzy0.5*(No. of tosses) - no. of heads.,

należy pamiętać, że chociaż różnica między rzeczywistą liczbą głów a oczekiwaną liczbą głów (50% liczby rzutów) wzrasta wraz ze wzrostem liczby rzutów, proporcja liczby głów do całkowitej liczby rzutów zbliża się do 0,5 (dla uczciwej monety).

ten eksperyment pokazuje nam bardzo częstą wadę występującą w podejściu frequentist tj. zależność wyniku eksperymentu od liczby powtórzeń eksperymentu.,

aby dowiedzieć się więcej o metodach statystycznych frequentist, możesz udać się na ten doskonały kurs statystyki wnioskowania.

nieodłączne wady statystyk Frequentist

do tej pory widzieliśmy tylko jedną wadę statystyk frequentist. To dopiero początek.

XX wiek odnotował ogromny wzrost statystyk częstotliwości stosowanych do modeli numerycznych w celu sprawdzenia, czy jedna próbka różni się od drugiej, parametr jest na tyle ważny, że może być zachowany w modelu i różne inne przejawy testowania hipotez., Ale częstokroć statystyki cierpiał kilka wielkich wad w jego konstrukcji i interpretacji, które stanowiły poważne zaniepokojenie we wszystkich rzeczywistych problemów życiowych. Na przykład:

p-values zmierzone w stosunku do próbki (o stałym rozmiarze) statystyki z pewnymi zmianami intencji zatrzymania ze zmianą intencji i rozmiaru próbki. tzn. jeśli dwie osoby pracują na tych samych danych i mają różne intencje zatrzymania, mogą uzyskać dwie różne p- values dla tych samych danych, co jest niepożądane.,

na przykład: osoba A może przestać rzucać monetą, gdy całkowita liczba osiągnie 100, A B zatrzyma się na 1000. Dla różnych rozmiarów próbek otrzymujemy różne wyniki t i różne wartości P. Podobnie, zamiar zatrzymania może zmienić się ze stałej liczby rzutów na całkowity czas rzutów. Również w tym przypadku musimy uzyskać różne wartości P.

2 – przedział ufności (C. I) jak p-value zależy w dużym stopniu od wielkości próbki., To sprawia, że potencjał zatrzymania jest absolutnie absurdalny, ponieważ bez względu na to, ile osób przeprowadzi testy na tych samych danych, wyniki powinny być spójne.

3 – przedziały ufności (C. I) nie są rozkładami prawdopodobieństwa, dlatego nie dostarczają najbardziej prawdopodobnej wartości dla parametru i najbardziej prawdopodobnych wartości.

te trzy powody są wystarczające, aby zachęcić Cię do myślenia o wadach podejścia frequentist i dlaczego istnieje potrzeba podejścia bayesowskiego. Przekonajmy się.,

stąd najpierw zrozumiemy podstawy bayesowskiej statystyki.

Statystyka bayesowska

„Statystyka bayesowska jest procedurą matematyczną, która stosuje prawdopodobieństwa do problemów statystycznych. Zapewnia ludziom narzędzia do aktualizacji ich przekonań w dowodach nowych danych.”

zrozumiałeś? Pozwól, że wyjaśnię to na przykładzie:

Załóżmy, że spośród wszystkich 4 wyścigów mistrzowskich (F1) pomiędzy Niki Laudą i Jamesem Huntem, Niki wygrał 3 razy, podczas gdy James zdołał tylko 1.,

więc, jeśli miałbyś postawić na zwycięzcę następnego wyścigu, kim by był ?

założę się, że powiesz Niki Lauda.

oto zwrot akcji. Co jeśli powiedziano ci, że padało raz, gdy wygrał James i raz, gdy wygrał Niki i jest pewne, że będzie padać w następnym dniu. Na kogo postawiłbyś teraz swoje pieniądze ?

intuicyjnie łatwo zauważyć, że szanse na wygraną Jamesa drastycznie wzrosły. Ale pytanie brzmi: ile ?,

aby zrozumieć problem, musimy zapoznać się z pewnymi pojęciami, z których pierwszym jest prawdopodobieństwo warunkowe (wyjaśnione poniżej).

ponadto istnieją pewne wymagania wstępne:

wymagania wstępne:

1. Algebra liniowa : aby odświeżyć podstawy, możesz sprawdzić algebrę Khan ' s Academy.
2. prawdopodobieństwo i podstawowe statystyki: aby odświeżyć podstawy, możesz sprawdzić inny kurs Khan Academy.

3.,1 prawdopodobieństwo warunkowe

jest ono zdefiniowane jako: prawdopodobieństwo zdarzenia a dane B jest równe prawdopodobieństwu wystąpienia B I a razem podzielonemu przez Prawdopodobieństwo B. ”

na przykład: załóżmy dwa częściowo przecinające się zestawy A i B, jak pokazano poniżej.

Set a reprezentuje jeden zestaw zdarzeń, a Set B inny. Chcemy obliczyć prawdopodobieństwo danego B już się stało. Pozwala reprezentować dzieje zdarzenia B przez cieniowanie go na Czerwono.,

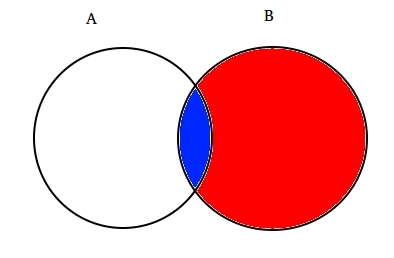
od kiedy B się stało, część, która teraz ma znaczenie dla A, jest częścią zacienioną na niebiesko, co jest interesujące . Tak więc, prawdopodobieństwo danego B okazuje się być:

dlatego możemy napisać wzór dla zdarzenia B podanego A już wystąpił przez:

lub

teraz drugie równanie można zapisać jako :

jest to znane jako Prawdopodobieństwo warunkowe.,

spróbujmy odpowiedzieć na problem z obstawianiem za pomocą tej techniki.

A być Zdarzenie deszczu. Dlatego

podstawiając wartości we wzorze prawdopodobieństwa warunkowego, otrzymujemy prawdopodobieństwo około 50%, co jest prawie podwójnym 25%, gdy deszcz nie był brany pod uwagę (Rozwiąż to na końcu).

to jeszcze bardziej wzmocniło nasze przekonanie o wygranej Jamesa w świetle nowych dowodów, tj. deszczu., Pewnie zastanawiasz się, że ta formuła jest bardzo podobna do czegoś, o czym mogłeś dużo słyszeć. Myśl!

prawdopodobnie, dobrze zgadłeś. Wygląda jak twierdzenie Bayesa.

twierdzenie Bayesa opiera się na prawdopodobieństwie warunkowym i leży w sercu wnioskowania bayesowskiego. Zrozummy to szczegółowo.

3.2 twierdzenie Bayesa

twierdzenie Bayesa wchodzi w życie, gdy wiele zdarzeń tworzy wyczerpujący zestaw z innym zdarzeniem B. Można to zrozumieć za pomocą poniższego diagramu.,

teraz B można zapisać jako

tak więc prawdopodobieństwo B można zapisać jako,

ale

tak, zastępując p(b) w równaniu prawdopodobieństwa warunkowego otrzymujemy

jest to równanie twierdzenia Bayesa.

wnioskowanie bayesowskie

nie ma sensu zagłębiać się w jej teoretyczny aspekt. Więc dowiemy się, jak to działa!, Weźmy przykład rzucania monetami, aby zrozumieć ideę wnioskowania bayesowskiego.

ważną częścią wnioskowania bayesowskiego jest ustalanie parametrów i modeli.

modele są matematycznym sformułowaniem obserwowanych zdarzeń. Parametry są czynnikami w modelach wpływającymi na obserwowane dane. Na przykład w rzucie monetą uczciwość monety może być zdefiniowana jako parametr monety oznaczony przez θ. Wynik zdarzenia może być oznaczony przez D.

Odpowiedz teraz., Jakie jest prawdopodobieństwo 4 Orłów z 9 rzutów (D) biorąc pod uwagę uczciwość monety (θ). i. E P(D|θ)

czekaj, czy zadałem właściwe pytanie? Nie.

powinniśmy być bardziej zainteresowani, wiedząc : biorąc pod uwagę wynik (D), jaka jest prawdopodobieństwo, że moneta jest uczciwa (θ=0.5)

przedstawimy ją za pomocą twierdzenia Bayesa:

P(θ|D)=(P(D|θ) X P(θ))/P(D)

tutaj, P(θ) jest przeorem tj. siłą naszej wiary w uczciwość monet przed rzutem., Jest całkowicie w porządku wierzyć, że moneta może mieć dowolny stopień uczciwości między 0 a 1.

P(D|θ) jest prawdopodobieństwem obserwacji naszego wyniku, biorąc pod uwagę nasz rozkład θ. Gdybyśmy wiedzieli, że moneta jest uczciwa, daje to prawdopodobieństwo obserwacji liczby Orłów w określonej liczbie rzutów.

P(D) jest dowodem. Jest to prawdopodobieństwo danych określone przez sumowanie (lub całkowanie) wszystkich możliwych wartości θ, ważone przez to, jak mocno wierzymy w te szczególne wartości θ.,

jeśli mieliśmy wiele poglądów na to, czym jest uczciwość monety (ale nie wiedzieliśmy na pewno), to mówi nam to prawdopodobieństwo zobaczenia pewnej sekwencji przewrotów dla wszystkich możliwości naszej wiary w uczciwość monety.

P(θ|D) polega na sprawdzeniu naszych parametrów po obserwacji dowodów tj. liczby głowic .

stąd zanurkujemy głębiej w Matematyczne implikacje tego pojęcia. Nie martw się. Gdy je zrozumiesz, dotarcie do matematyki jest dość łatwe.,

aby poprawnie zdefiniować nasz model , potrzebujemy przed ręką dwóch modeli matematycznych. Jeden do reprezentowania funkcji prawdopodobieństwa P (D / θ), a drugi do reprezentowania rozkładu wcześniejszych przekonań . Iloczyn tych dwóch daje rozkład P(θ|D).

ponieważ zarówno wcześniejsze, jak i tylne są przekonaniami o dystrybucji uczciwości monet, intuicja mówi nam, że oba powinny mieć tę samą formę matematyczną. Pamiętaj o tym. Wrócimy do tego jeszcze raz.,

istnieje więc kilka funkcji wspierających istnienie twierdzenia Bayesa. Znajomość ich jest ważna, dlatego wyjaśniłem je szczegółowo.

4.1. Funkcja prawdopodobieństwa Bernoulliego

podsumujmy to, czego dowiedzieliśmy się o funkcji prawdopodobieństwa. Dowiedzieliśmy się więc, że:

jest to prawdopodobieństwo obserwacji określonej liczby Orłów w określonej liczbie rzutów dla danej uczciwości monety. Oznacza to, że nasze prawdopodobieństwo obserwacji Orzeł / reszka zależy od uczciwości monety (θ).,

P(y=1|θ)=

P(y=0|θ)=

warto zauważyć, że reprezentowanie 1 jako głów i 0 jako ogonów jest tylko notacją matematyczną do sformułowania modelu. Możemy połączyć powyższe definicje matematyczne w jedną definicję, aby reprezentować prawdopodobieństwo obu wyników.

P(y/θ)=

nazywa się to funkcją prawdopodobieństwa Bernoulliego, a zadanie rzutu monetą nazywa się próbami Bernoulliego.,

y={0,1},θ=(0,1)

a gdy chcemy zobaczyć serię głów lub przewróceń, prawdopodobieństwo ich wystąpienia jest podane przez:

ponadto, jeśli interesuje nas prawdopodobieństwo pojawienia się liczby głowic z W N liczbie przewrotów, to prawdopodobieństwo jest podane przez:

4.2. Wcześniejsza Dystrybucja przekonań

ta dystrybucja jest używana do reprezentowania naszych mocnych stron w przekonaniach o parametrach opartych na wcześniejszym doświadczeniu.,

ale co jeśli ktoś nie ma wcześniej doświadczenia?

nie martw się. Matematycy opracowali metody łagodzenia tego problemu. Jest znany jako uninformative priors. Chciałbym z góry poinformować, że jest to po prostu błędna nazwa. Każdy niedoinformowany przeor zawsze dostarcza jakiejś informacji o stałym rozkładzie przeora.

funkcja matematyczna używana do reprezentowania wcześniejszych przekonań jest znana jako beta distribution., Ma bardzo ładne właściwości matematyczne, które pozwalają nam modelować nasze przekonania na temat rozkładu dwumianowego.

funkcja gęstości prawdopodobieństwa rozkładu beta ma postać:

gdzie skupiamy się na liczniku. Mianownik jest tam tylko po to, aby upewnić się, że całkowita funkcja gęstości prawdopodobieństwa po całkowaniu ocenia się na 1.

α Iβ nazywane są parametrami decydującymi o kształcie funkcji gęstości., Tutaj α jest analogiczne do liczby głowic w próbach, a β odpowiada liczbie ogonów., Poniższe diagramy pomogą Ci zobrazować dystrybucje beta dla różnych wartości α I β

Możesz również narysować dystrybucję beta dla siebie, używając następującego kodu w R:

uwaga: α I β są intuicyjne do zrozumienia, ponieważ można je obliczyć znając średnią (μ) i odchylenie standardowe (σ) rozkładu., W rzeczywistości są one powiązane jako:

Jeśli znane są średnie i odchylenie standardowe rozkładu , wówczas parametry kształtu można łatwo obliczyć.

wnioskowanie wyciągnięte z wykresów powyżej:

1. gdy nie było rzutu wierzyliśmy, że każda uczciwość monety jest możliwa, jak to przedstawia płaska linia.
2. gdy była większa liczba Orłów niż Reszki, Wykres pokazywał szczyt przesunięty w kierunku prawej strony, co wskazywało na większe prawdopodobieństwo orłów i że moneta nie jest sprawiedliwa.,
3. ponieważ robi się więcej rzutów, a głowy nadal przybywają w większej proporcji, szczyt zwęża się, zwiększając nasze zaufanie do uczciwości wartości monety.

4.3. Posterior Belief Distribution

powodem, dla którego wybraliśmy wcześniejsze przekonanie, jest uzyskanie dystrybucji beta. Dzieje się tak dlatego, że gdy mnożymy go przez funkcję prawdopodobieństwa, rozkład tylny daje formę podobną do rozkładu poprzedniego, która jest znacznie łatwiejsza do odniesienia i zrozumienia., Jeśli taka ilość informacji zaostrzy Twój apetyt, jestem pewien, że jesteś gotowy, aby przejść dodatkową milę.

obliczmy za pomocą twierdzenia Bayesa.

Obliczanie tylnego przekonania za pomocą twierdzenia Bayesa

teraz nasze tylne przekonanie staje się,

to jest ciekawe., Po prostu znając średni i standardowy rozkład naszego przekonania o parametrze θ I obserwując liczbę głowic W N flip, możemy zaktualizować nasze przekonanie o parametrze modelu(θ).

pozwala to zrozumieć za pomocą prostego przykładu:

Załóżmy, że uważasz, że moneta jest stronnicza. Ma średnie odchylenie (μ) około 0,6 z odchyleniem standardowym 0,1.

α= 13.8,β=9.2

i.,e nasza dystrybucja będzie stronnicza po prawej stronie. Załóżmy, że zaobserwowałeś 80 głów (z=80) w 100 przewrotkach (N=100). Zobaczmy, jak będą wyglądać nasze wcześniejsze i tylne przekonania:

prior = P(θ|α,β)=P(θ|13.8,9.2)

Posterior = P(θ|z+α,N-z+β)=P(θ|93.8,29.2)

pozwala wizualizować obie przekonania na wykresie:

kod R dla powyższego wykresu jest następujący:

}

ponieważ robi się coraz więcej przewrotek i obserwuje się nowe dane, nasze przekonania są aktualizowane., To jest prawdziwa moc wnioskowania bayesowskiego.

Test na znaczenie – Frequentist vs Bayesian

bez wchodzenia w rygorystyczne struktury matematyczne, Ta sekcja dostarczy Ci szybki przegląd różnych podejść metod frequentist i bayesian do badania znaczenia i różnicy między grupami i Która metoda jest najbardziej wiarygodna.

5.1. wartość p

w tym przypadku oblicza się wynik T dla konkretnej próbki z rozkładu próbkowania o stałej wielkości. Następnie przewidywane są wartości P., Możemy interpretować wartości p jako (biorąc przykład wartości P jako 0.02 dla rozkładu średniej 100): istnieje 2% prawdopodobieństwo, że próbka będzie miała średnią równą 100.

ta interpretacja cierpi z powodu wady, że dla rozkładów próbkowania o różnych rozmiarach, jeden jest zobowiązany do uzyskania innego t-score, a tym samym inna wartość p. To absurd. Wartość p mniejsza niż 5% nie gwarantuje, że hipoteza zerowa jest zła ani wartość p większa niż 5% zapewnia, że hipoteza zerowa jest słuszna.

5.2., Przedziały ufności

przedziały ufności również cierpią z powodu tej samej wady. Ponadto, ponieważ C. I nie jest rozkładem prawdopodobieństwa, nie ma sposobu, aby dowiedzieć się, które wartości są najbardziej prawdopodobne.

5.3. Współczynnik Bayesa

współczynnik Bayesa jest odpowiednikiem wartości p w strukturze Bayesa. Pozwala zrozumieć go w sposób kompleksowy.

hipoteza zerowa w ramach bayesowskiej zakłada ∞ rozkład prawdopodobieństwa tylko przy określonej wartości parametru (powiedzmy θ=0.5) i zerowym prawdopodobieństwie gdzie indziej., (M1)

alternatywna hipoteza jest taka, że wszystkie wartości θ są możliwe, stąd płaska krzywa reprezentująca rozkład. (M2)

teraz rozkład nowych danych wygląda jak poniżej.

Statystyka bayesowska skorygowała wiarygodność (prawdopodobieństwo) różnych wartości θ. Łatwo zauważyć, że rozkład prawdopodobieństwa przesunął się w kierunku M2 o wartości wyższej niż M1, tj. M2 jest bardziej prawdopodobne.,

współczynnik Bayesa nie zależy od rzeczywistych wartości rozkładu θ, ale wielkości przesunięcia wartości M1 i M2.

w panelu A (pokazano powyżej): lewy pasek (M1) jest wcześniejsze prawdopodobieństwo hipotezy zerowej.

w panelu B (pokazano), lewy pasek jest tylne prawdopodobieństwo hipotezy zerowej.

współczynnik Bayesa jest zdefiniowany jako stosunek kursów tylnych do kursów wcześniejszych,

aby odrzucić hipotezę zerową, preferowany jest współczynnik BF < 1/10.,

możemy zobaczyć natychmiastowe korzyści z używania czynnika Bayesa zamiast wartości p, ponieważ są one niezależne od intencji i wielkości próbki.

5.4. Przedział wysokiej gęstości (HDI)

HDI powstaje z rozkładu tylnego po obserwacji nowych danych. Ponieważ HDI jest prawdopodobieństwem, 95% HDI daje 95% najbardziej wiarygodnych wartości. Jest również gwarantowane, że 95% wartości będzie leżeć w tym przedziale w przeciwieństwie do ci

zauważ, jak 95% HDI w dystrybucji wcześniejszej jest szerszy niż 95% dystrybucji tylnej., Dzieje się tak dlatego, że nasza wiara w HDI wzrasta wraz z obserwacją nowych danych.

Uwagi końcowe

celem tego artykułu było zachęcenie Cię do zastanowienia się nad różnymi rodzajami filozofii statystycznych i tym, jak żadna z nich nie może być używana w każdej sytuacji.

najwyższy czas, aby obie filozofie zostały połączone, aby złagodzić rzeczywiste problemy, rozwiązując wady innych., Część II tej serii koncentruje się na technikach redukcji wymiarów przy użyciu algorytmów MCMC (Markov Chain Monte Carlo). Część III będzie oparta na tworzeniu bayesowskiego modelu regresji od podstaw i interpretacji jego wyników w R. więc, zanim zacznę od części II, chciałbym mieć swoje sugestie / opinie na temat tego artykułu.