w tej lekcji zbudujemy pięć (5) wspólnych logicznych połączeń lub operatorów. Są one uważane za wspólne logiczne powiązania, ponieważ są bardzo popularne, użyteczne i zawsze nauczane razem.
zanim zaczniemy, proponuję przejrzeć moją drugą lekcję, w której link znajduje się poniżej.
Ta lekcja wprowadzająca o tablicach prawdy zawiera niezbędną wiedzę lub informacje, które pomogą Ci lepiej zrozumieć treść tej lekcji.,
Wprowadzenie do tabel prawdy, stwierdzeń i Konectives
le ' S rozpocząć od wymieniając pięć (5) wspólnych logicznych konectives.
Pięć (5) wspólnych logicznych koneksji lub operatorów
- negacja logiczna
- logiczna Koniunkcja (and)
- logiczna Dysjunkcja (Inclusive OR)
- logiczna implikacja (warunkowa)
- logiczna Dwuwątkowa (Podwójna implikacja)
I., Tablica prawdy negacji logicznej
negacja twierdzenia jest również stwierdzeniem o wartości prawdy, która jest dokładnie odwrotna do pierwotnej twierdzenia. Na przykład negacja wyrażenia jest zapisywana symbolicznie jako
~\large{P} lub \large{\neg P}.
~{p} lub {\neg P} jest odczytywane jako „nie P.”
pamiętaj: operator negacji oznaczony symbolem ~ lub \neg pobiera wartość prawdy oryginalnej instrukcji, a następnie wypisuje dokładną odwrotność jej wartości prawdy., Innymi słowy, negacja po prostu Odwraca wartość prawdy danego stwierdzenia. Tak więc, jeśli twierdzenie P jest prawdziwe, to wartość prawdy jego negacji jest fałszywa. W ten sam sposób, jeśli P jest fałszywe, wartość jego negacji jest prawdziwa.

centrala. ,
symbolem, który jest używany do reprezentowania operatora logicznego and or jest \ color{red}\Large {\wedge}. Wygląda jak odwrócona litera V.
Jeśli mamy dwa proste wyrażenia P I Q i chcemy utworzyć złożone wyrażenie połączone operatorem AND, możemy zapisać je jako:
\large{P \wedge Q}.
{p \wedge Q} jest odczytywane jako „P i q”.
pamiętaj: wartość prawdy złożonego wyrażenia P \wedge Q Jest Prawdziwa tylko wtedy, gdy wartości prawdy P I Q są prawdziwe., W przeciwnym wypadku P \klin Q jest false.
zauważ w poniższej tabeli prawdy, że gdy P jest prawdą, a Q jest prawdą, to P \ klin Q jest prawdą. Pozostałe trzy kombinacje twierdzeń P I Q są jednak fałszywe.

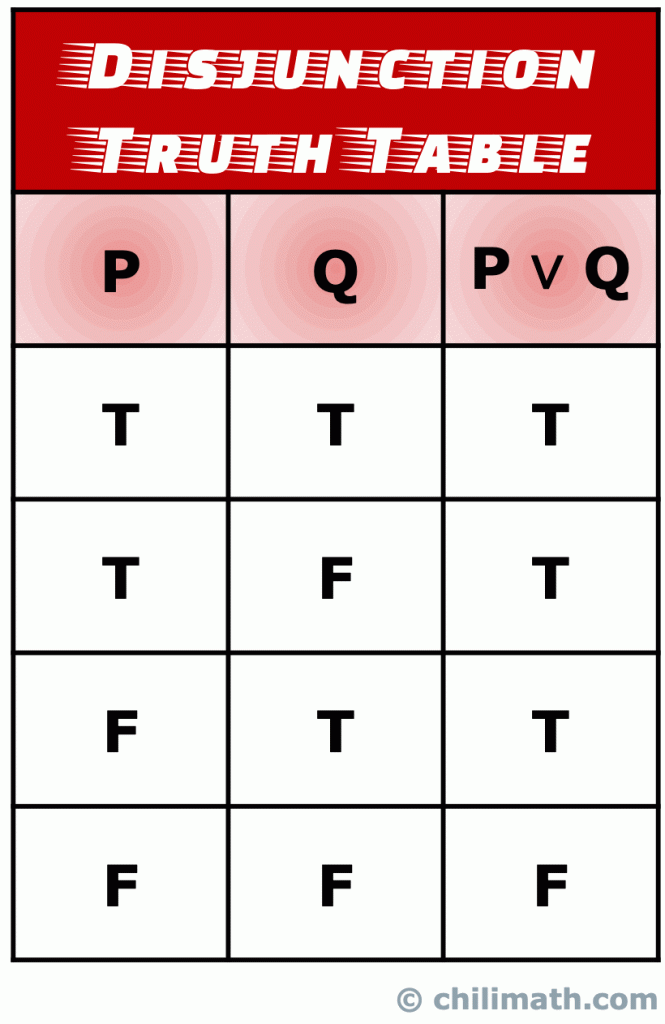
III. tablica prawdy logicznej Dysjunkcji
dysjunkcja jest rodzajem złożonej instrukcji, która składa się z dwóch prostych instrukcji utworzonych przez połączenie instrukcji z Operator sali operacyjnej.
w instrukcji disjunction, użycie OR jest inclusive. To znaczy „jedno albo drugie” albo jedno i drugie.,
symbolem używanym do reprezentowania operatora dysjunkcji logicznej OR or jest \ color{red}\Large {\vee}. Przypomina literę V alfabetu.
dwie propozycje P I Q połączone operatorem OR tworząc złożone wyrażenie jest zapisywane jako:
\large{P \Vee Q}.
{p \Vee Q} jest odczytywane jako „P lub q”.
pamiętaj: wartość prawdy złożonego wyrażenia P \ Vee Q Jest Prawdziwa, jeśli wartość prawdy dwóch prostych wyrażeń P I Q Jest Prawdziwa., Moreso, P \vee Q jest również prawdziwe, gdy wartości prawdy obu twierdzeń P I Q są prawdziwe. Jednak tylko wtedy, gdy twierdzenie dyjunkcji P \vee Q jest fałszywe, dzieje się, gdy wartości prawdy zarówno P, jak i Q są fałszywe.
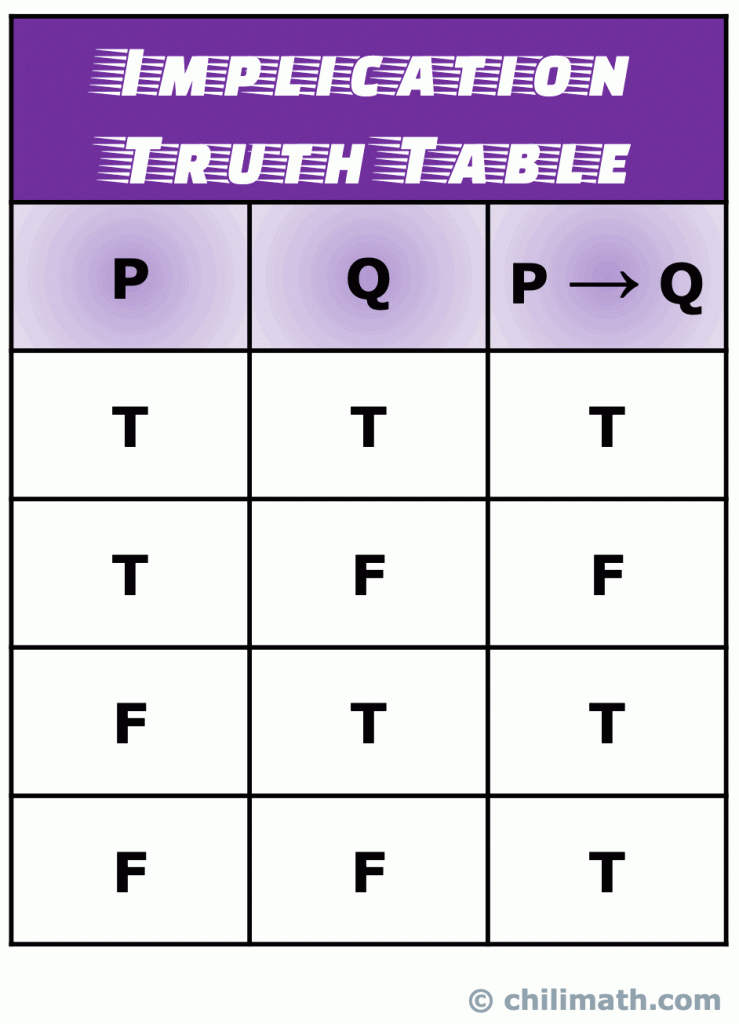
IV. tablica prawdy implikacji logicznej
implikacja (znana również jako instrukcja warunkowa) jest typem złożonej instrukcji, która jest utworzona przez połączenie dwóch prostych wypowiedzi z implikacją logiczną lub operatorem.,
symbolem używanym do reprezentowania operatora implikacji logicznej jest strzałka skierowana w prawo, a więc strzałka w prawo.

gdy dwa proste wyrażenia P I Q są połączone operatorem implikacji, mamy:
\large{P \to Q}.
- gdzie p jest znany jako hipoteza
- gdzie Q jest znany jako wniosek
istnieje wiele sposobów odczytu warunkowego {p \do Q}., Poniżej znajdują się niektóre z niewielu popularnych.
pamiętaj: wartość prawdy złożonego wyrażenia p \do Q Jest Prawdziwa, gdy zarówno proste wyrażenia P, jak i Q są prawdziwe. Moreso, p \To Q jest zawsze prawdziwe, jeśli p jest fałszywe. Jedyny scenariusz, że p \do Q jest false, dzieje się wtedy, gdy p jest true, A Q jest false.
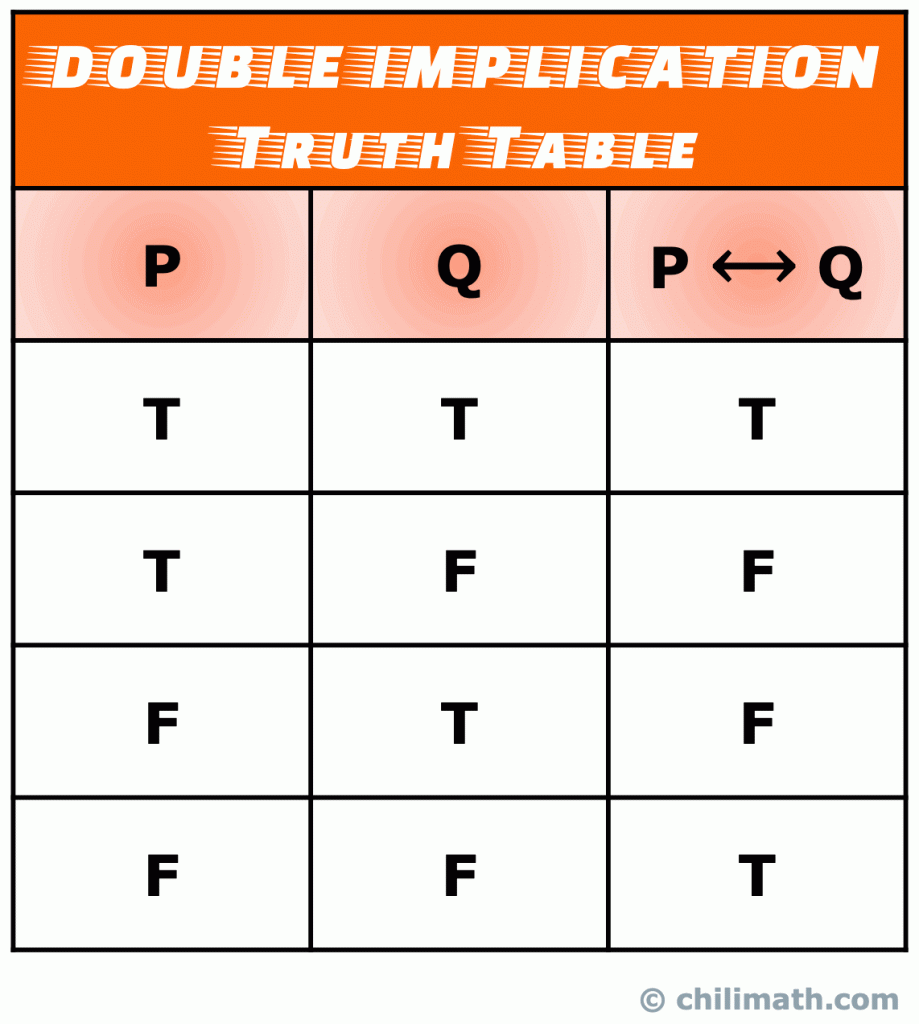
V., Tablica prawdy logicznej dwujęzycznej lub podwójnej implikacji
implikacja Podwójna (znana również jako deklaracja dwujęzyczna) jest rodzajem złożonego oświadczenia, które powstaje przez połączenie dwóch prostych wyrażeń z operatorem dwujęzycznym. Dwukondygnacyjna wypowiedź jest tak naprawdę kombinacją instrukcji warunkowej i jej converse.
operator dwugłowy oznaczany jest strzałką dwugłową.,

Po połączeniu dwóch prostych instrukcji (znanych również jako instrukcje molekularne) z operatorem dwukondygnacyjnym otrzymujemy:
\large{P \leftrighttarrow q}
{p \leftrighttarrow Q} jest odczytywane jako „p wtedy i tylko wtedy, gdy Q.,”
- gdzie P jest znane jako poprzedzające
- gdzie Q jest znane jako następcze
pamiętaj: wartość prawdy dwuwartościowej instrukcji P \leftrighttarrow Q Jest Prawdziwa, gdy obie proste instrukcje P I Q są zarówno prawdziwe, jak i fałszywe. W przeciwnym wypadku, P \leftrighttarrow Q jest false.
Możesz być również zainteresowany:
Wprowadzenie do tabel prawdy, twierdzeń i logicznych połączeń
Converse, Inverse i contrapositive instrukcji warunkowej
Dodaj komentarz