jednym z najbardziej znanych wzorów matematycznych jest twierdzenie Pitagorasa, które dostarcza nam relacji między bokami w trójkącie prostym. Trójkąt prostokątny składa się z dwóch nóg i przeciwprostokątnej. Dwie nogi spotykają się pod kątem 90°, a przeciwprostokątna jest najdłuższym bokiem trójkąta prostego i jest stroną przeciwną kątowi prostemu.,
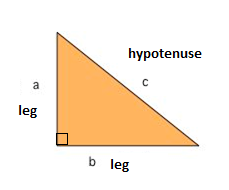
twierdzenie Pitagorasa mówi nam, że relacja w każdym trójkącie prostym wynosi:
$$a^{2}+b^{2}=c^{2}$$
przykład
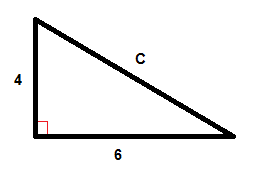
$$c^{2}=6^{2}+4^{2}$$
$$C^{2}=36+16$$
$$C^{2}=52$$
$ $ c=\sqrt{52}$$
$$c \ approx 7.2$$
istnieje kilka specjalnych rodzajów trójkątów prostokątnych, takich jak Trójkąty prostokątne 45°-45° i trójkąt prostokątny 30°-60°.,
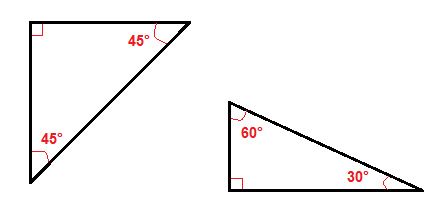
ze względu na ich kąty łatwiej jest znaleźć przeciwprostokątną lub nogi w tych trójkątach prawych niż we wszystkich innych trójkątach prawych.
w trójkącie prostokątnym 45°-45° wystarczy pomnożyć jedną nogę przez √2, aby uzyskać długość przeciwprostokątnej.
przykład
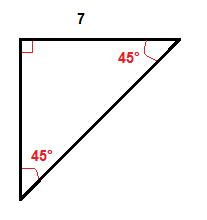
mnożymy długość nogi, która wynosi 7 cali przez √2, aby uzyskać długość przeciwprostokątnej.
$$7\cdot \sqrt{2}\approx 9.,9$$
w trójkącie prostym 30°-60° możemy znaleźć długość nogi, która jest przeciwna kątowi 30°, używając tej formuły:
$$a=\frac{1}{2}\cdot c$$
przykład
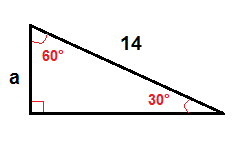
aby znaleźć a, używamy powyższej formuły.
$$a= \ frac{1} {2} \ cdot 14$$
$$a=7$$
lekcja wideo
Znajdź boki tego trójkąta prostokątnego
Dodaj komentarz