|
“Bi” significa “dois” (como uma bicicleta tem duas rodas) … |
 |

Jogando uma Moeda:
- conseguimos Cabeças (H) ou
- Caudas (T)
Podemos dizer que a probabilidade de a moeda de destino H ½
E a probabilidade de a moeda de destino T ½
Vamos jogar uma Moeda!Atira uma moeda justa três vezes … Qual é a hipótese de ganhar duas cabeças?,tr>
THH



THT



TTH



TTT



Which outcomes do we want?,












“duas cabeças” podem estar em qualquer ordem:” HHT”,” THH “e” HTH ” todos têm duas cabeças (e uma cauda).
So 3 of the outcomes produce “Two Heads”.
Qual é a probabilidade de cada resultado?,ções são (P significa “Probabilidade”):
- P(Três Cabeças) = P(HHH) = 1/8
- P(Duas Cabeças) = P(HHT) + P(HTH) + P(THH) = 1/8 + 1/8 + 1/8 = 3/8
- P(a Cabeça) = P(HTT) + P(THT) + P(TTH) = 1/8 + 1/8 + 1/8 = 3/8
- P(Zero Cabeças) = P(TTT) = 1/8
podemos escrever isso em termos de uma Variável Aleatória, X, = “O número de Cabeças de 3 jogadas de uma moeda”:
- P(X = 3) = 1/8
- P(X = 2) = 3/8
- P(X = 1) = 3/8
- P(X = 0) = 1/8
E este é o que parece como um gráfico:
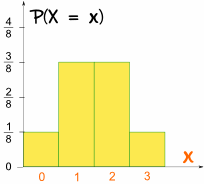
é simétrica!,
fazendo uma fórmula
Agora imagine que queremos as chances de 5 cabeças em 9 tosses: para listar todos os 512 resultados vai demorar muito tempo! então vamos fazer uma fórmula.
no nosso exemplo anterior, como podemos obter os valores 1, 3, 3 e 1 ?
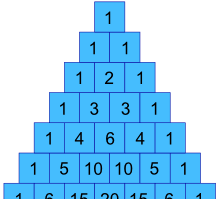
bem, eles estão realmente no Triângulo de Pascal !podemos fazê-los usando uma fórmula?
a Certeza que estamos, e aqui está ele:
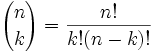
é muitas vezes chamado de “n k”
- n = número total
- k = o número que você quiser
- “!,”significa ” factorial”, por exemplo 4! = 1×2×3×4 = 24
pode ler mais sobre ele em combinações e permutações.
Let’s try it:
Let’s use it for a harder question:
Bias!
até agora as chances de sucesso ou fracasso têm sido igualmente prováveis.
mas e se as moedas são tendenciosas (terra mais de um lado do que outro) ou as escolhas não são 50/50.exemplo: vende sanduíches. 70% das pessoas escolhem frango, os outros escolhem outra coisa.
isto é como o exemplo da cabeça e caudas, mas com 70/30 em vez de 50/50.,
Vamos desenhar um diagrama de árvore:
Os Dois “Frango” casos são realçados.
as probabilidades para “dois frangos” todas se tornam 0,147, porque estamos multiplicando dois 0,7 s e um 0,3 em cada caso. Em outras palavras
0.147 = 0.7 × 0.7 × 0.3
Ou, usando expoentes:
= 0.72 × 0.31
0,7 é a probabilidade de cada escolha que quiser, chame-a de p
O 2 é o número de escolhas que quiser, chame-a de k
E temos (até agora):
= pk × 0.31
A 0.,3 é a probabilidade de o oposto de escolha, portanto, é: 1−p
O 1 é o número de oposto escolhas, portanto, é: n−k
o Que nos dá:
= pk(1-p)(n-k)
Onde
- p é a probabilidade de cada escolha queremos
- k é o número de escolhas que nós queremos
- n é o número total de escolhas
Agora sabemos que a probabilidade de cada resultado é 0.147
OK. Foi muito trabalho para algo que já sabíamos, mas agora temos uma fórmula que podemos usar para perguntas mais difíceis.,
reunindo
Agora sabemos como calcular quantos:
n!k!(n-k)!
E a probabilidade de cada:
pk(1-p)(n-k)
Quando multiplicados juntos podemos obter:
a Probabilidade de k de n maneiras:
P(k de n) = n!k!(n-k)! pk(1-p)(n-k)
A Geral Binomial de Probabilidade, a Fórmula
Notas Importantes:
- Os ensaios são independentes,
- Existem apenas dois resultados possíveis em cada prova,
- A probabilidade de “sucesso” em cada avaliação é constante.,
Quincunce

Tem uma brincadeira com o Quincunce (então leia Quincunce Explicado) para ver a Distribuição Binomial em ação.
Jogar a Morrer
Um justo morrer é lançada quatro vezes. Calcular as probabilidades de obter:
- 0 Pares
- 1 Dois
- 2 Pares
- 3 Pares
- 4 Pares
neste caso n=4, p = P(Duas) = 1/6
X é a Variável Aleatória “Número de Pares de quatro lança’.,
Substituto x = 0 a 4 na fórmula:
P(K fora de n) = n!k!(n-k)! pk(1-p)(n-k)
Como esta (4 casas decimais):
Desta vez, o gráfico não é simétrica:
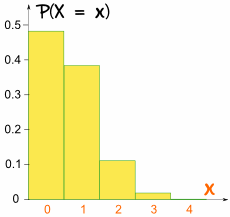
não é simétrica!
está inclinado porque p não é 0,5

bicicletas de desporto
a sua empresa fabrica bicicletas de desporto. 90% passam na inspeção final (e 10% falham e precisam ser fixados).
Qual é a média esperada e a variância das 4 próximas inspecções?primeiro, vamos calcular todas as probabilidades.,
- n = 4,
- p = p(Pass) = 0, 9
X é a variável aleatória “número de passes de quatro inspecções”.
Substituto x = 0 a 4 na fórmula:
P(K fora de n) = n!k!(n-k)! pk(1-p) (n-k)
média, variância e desvio-padrão
vamos calcular a média, variância e desvio-padrão para as inspecções de bicicletas desportivas.
existem (relativamente) fórmulas simples para eles. São um pouco difíceis de provar, mas funcionam!,
A média ou “valor esperado”, é a seguinte:
µ = np
A fórmula para a Variância é:
Variância: σ2 = np(1-p)
E o Desvio Padrão é a raiz quadrada da variância:
σ = √(np(1-p))
Para a prática de desportos de bicicletas:
Variância: σ2 = 4 × 0.9 × 0.1 = 0.36
o Desvio-Padrão é:
σ = √(0.36) = 0.6


Deixe uma resposta