Estatística Bayesiana explicado para Iniciantes em inglês Simples

Descrição

• As desvantagens de freqüentista estatísticas de levar para a necessidade de Estatística Bayesiana
• Descubra Estatística Bayesiana e da Inferência Bayesiana
• Existem vários métodos para testar a significância do modelo, como o valor de p, intervalo de confiança, etc

Introdução

Estatística Bayesiana continua a ser incompreensível a inflamar as mentes de muitos analistas., Espantados com o incrível poder da aprendizagem de máquinas, muitos de nós tornaram-se infiéis às estatísticas. O nosso foco limitou-se a explorar a aprendizagem de máquinas. Não é verdade?

we fail to understand that machine learning is not the only way to solve real world problems. Em várias situações, não nos ajuda a resolver problemas de negócios, embora haja dados envolvidos nesses problemas. No mínimo, o conhecimento de estatísticas permitir-lhe-á trabalhar em problemas analíticos complexos, independentemente da dimensão dos dados.,

In 1770s, Thomas Bayes introduced ‘Bayes Theorem’. Mesmo depois de séculos mais tarde, a importância das “estatísticas Bayesianas” não desapareceu. De fato, hoje este tema está sendo ensinado em grandes profundidades em algumas das principais universidades do mundo.

com esta ideia, criei este guia de Iniciantes sobre estatísticas Bayesianas. Eu tentei explicar os conceitos de uma maneira simplista com exemplos. É desejável o conhecimento prévio da probabilidade básica & estatísticas., Você deve verificar este curso para obter uma baixa abrangente nas estatísticas e probabilidades.

no final deste artigo, você terá uma compreensão concreta das estatísticas Bayesianas e seus conceitos associados.,>Teorema de Bayes

Inferência Bayesiana

• Bernoulli probabilidade de função
• Antes de Crença de Distribuição
• Posterior crença de Distribuição

Teste de Significância – Freqüentista vs Bayesiana

• p-valor
• Intervalos de Confiança
• Fator de Bayes
• de Alta Densidade Intervalo (IDH)

Antes de realmente mergulhar na Estatística Bayesiana, vamos gastar alguns minutos a compreensão Freqüentista de Estatísticas, a versão mais popular de estatísticas, a maioria de nós deparamos e os problemas inerentes a isso.,

Frequentist Statistics

the debate between frequentist and bayesian have haunted beginners for centuries. Portanto, é importante entender a diferença entre os dois e como existe uma fina linha de demarcação!

é a técnica inferencial mais amplamente utilizada no mundo estatístico. Na verdade, geralmente é a primeira escola de pensamento que uma pessoa que entra no mundo das estatísticas se depara.

Frequentist Statistics tests whether an event (hypothesis) occurs or not., Calcula a probabilidade de um evento a longo prazo da experiência (ou seja, a experiência é repetida nas mesmas condições para obter o resultado).

aqui, as distribuições de amostragem de tamanho fixo são tomadas. Então, o experimento é teoricamente repetido infinitamente número de vezes, mas praticamente feito com uma intenção de parada. Por exemplo, eu realizo uma experiência com uma intenção de parar em mente que eu vou parar a experiência quando ela é repetida 1000 vezes ou eu vejo no mínimo 300 cabeças em um lançamento de moeda.

vamos mais fundo agora.,

agora, vamos entender estatísticas freqüentes usando um exemplo de lançamento de moeda. O objectivo é estimar a equidade da moeda. Abaixo está uma tabela que representa a frequência das cabeças:

sabemos que a probabilidade de obter uma cabeça ao atirar uma moeda justa é de 0,5. No. of heads representa o número real de cabeças obtidas. Difference é a diferença entre 0.5*(No. of tosses) - no. of heads.,

Uma coisa importante é notar que, embora a diferença entre o número de cabeças e o número esperado de cabeças( 50% do número de jogadas) aumenta à medida que o número de jogadas aumentado, a proporção do número de cabeças número total de jogadas abordagens de 0,5 (para uma feira de moeda).

esta experiência apresenta-nos uma falha muito comum encontrada na abordagem frequente, ou seja, dependência do resultado de uma experiência do número de vezes que a experiência é repetida.,

para saber mais sobre métodos estatísticos freqüentistas, você pode ir para este excelente curso sobre estatísticas inferenciais.

as falhas inerentes nas estatísticas de Frequência

até aqui, vimos apenas uma falha nas estatísticas de frequência. Bem, É só o começo.

século 20 viu um enorme aumento no freqüentista estatísticas ser aplicado para modelos numéricos para verificar se uma amostra é diferente do outro, um parâmetro é importante o suficiente para ser mantido no modelo e variousother manifestações de testes de hipóteses., Mas estatísticas freqüentes sofreram algumas grandes falhas em sua concepção e interpretação, o que colocou uma séria preocupação em todos os problemas da vida real. Por exemplo:

p-values medido em relação a uma estatística de amostra (tamanho fixo), com algumas mudanças de intenção de paragem com alteração na intenção e tamanho da amostra. ou seja, se duas pessoas trabalham com os mesmos dados e têm uma intenção de paragem diferente, podem obter dois p- values para os mesmos dados, o que é indesejável.,

por exemplo: a pessoa a pode optar por parar de atirar uma moeda quando a contagem total atingir 100, enquanto B pára em 1000. Para diferentes tamanhos de amostra, temos diferentes pontuações t e diferentes valores p. Da mesma forma, a intenção de parar pode mudar de número fixo de flips para a duração total de flipping. Também neste caso, estamos obrigados a obter valores p diferentes.

2 – Intervalo de Confiança (C. I) como o p-value depende fortemente do tamanho da amostra., Isso torna o potencial de parada absolutamente absurdo, uma vez que não importa quantas pessoas executam os testes com os mesmos dados, os resultados devem ser consistentes.

3 – intervalos de confiança (C. I) não são distribuições de probabilidade, portanto não fornecem o valor mais provável para um parâmetro e os valores mais prováveis.

estas três razões são suficientes para levá-lo a pensar sobre os inconvenientes da abordagem freqüente e por que há uma necessidade de abordagem Bayesiana. Vamos descobrir.,a partir daqui, vamos primeiro entender os conceitos básicos das estatísticas Bayesianas.

Estatísticas Bayesianas

“Estatísticas Bayesianas é um procedimento matemático que aplica probabilidades a problemas estatísticos. Ele fornece às pessoas as ferramentas para atualizar suas crenças na evidência de novos dados.percebeste? Deixe-me explicar com um exemplo:

Suponha que, de todas as 4 provas do campeonato (F1) entre Niki Lauda e James hunt, Niki ganhou 3 vezes enquanto James conseguiu apenas 1.,então, se apostasse no vencedor da próxima corrida, quem seria ele ?aposto que diria Niki Lauda.

aqui está o twist. E se lhe disserem que choveu uma vez quando James ganhou e uma vez quando Niki ganhou e é definitivo que choverá na próxima data? Então, em quem apostarias o teu dinheiro agora ?

por intuição, é fácil ver que as chances de ganhar para James aumentaram drasticamente. Mas a questão é: quanto ?,

para compreender o problema em mãos, precisamos nos familiarizar com alguns conceitos, primeiro dos quais é a probabilidade condicional (explicada abaixo).

além disso, existem certos pré-requisitos:

pré-requisitos:

1. Álgebra Linear : para atualizar seus conceitos básicos, você pode verificar a álgebra da Academia de Khan.
2. Probabilidade e estatísticas básicas: para atualizar o seu básico, você pode verificar outro curso pela Khan Academy.

3.,1 Probabilidade Condicional

é definido como: Probabilidade de um evento A dado B é igual a probabilidade de B e Um a acontecer juntos, dividida pela probabilidade de B.”

Por exemplo: Suponha que dois parcialmente a interseção de conjuntos A e B, como mostrado abaixo.

O conjunto a representa um conjunto de eventos e o conjunto B representa outro. Queremos calcular a probabilidade de um dado B já ter acontecido. Vamos representar o acontecimento do evento B sombreando-o com vermelho.,

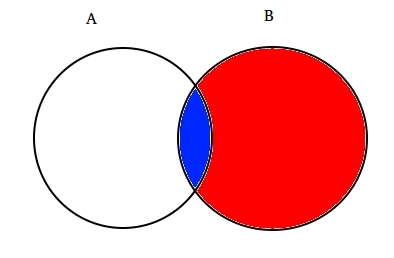
Agora que B aconteceu, a parte que agora importa para A é a parte sombreada em azul que é interessante . Assim, a probabilidade de A dado B passa a ser:

Portanto, podemos escrever a fórmula para o evento de B dado Um que já tenha ocorrido por:

ou

Agora, a segunda equação pode ser reescrita como :

Este é conhecido como Probabilidade Condicional.,

vamos tentar responder a um problema de apostas com esta técnica.suponha que B seja o evento da vitória de James Hunt. A be the event of raining. Portanto,

substituindo os valores na fórmula de probabilidade condicional, obtemos a probabilidade de ser cerca de 50%, que é quase o dobro de 25% quando a chuva não foi levada em conta (resolvê-la no seu fim).

This further strengthened our belief of James winning in the light of new evidence I. E. rain., Deves estar a pensar que esta fórmula se parece muito com algo de que deves ter ouvido falar muito. Pensa!provavelmente, acertaste. Parece o teorema de Bayes.

Bayes theorem is built on top of conditional probability and lies in the heart of Bayesian Inference. Vamos entender isso em detalhes agora.

3.2 Teorema de Bayes

Teorema de Bayes entra em vigor quando vários eventos formam um conjunto exaustivo com outro evento B. Isto pode ser compreendido com a ajuda do diagrama abaixo.,

Agora, B pode ser escrito como

Então, a probabilidade de B pode ser escrita como,

Mas

Então, substituindo P(B) na equação da probabilidade condicional temos

Esta é a equação do Teorema de Bayes.

Inferência Bayesiana

não faz sentido mergulhar no aspecto teórico da mesma. Então, vamos aprender como funciona!, Tomemos um exemplo de atirar moedas para entender a ideia por trás da Inferência Bayesiana.

Uma parte importante da inferência bayesiana é o estabelecimento de parâmetros e modelos.

modelos são a formulação matemática dos eventos observados. Os parâmetros são os fatores nos modelos que afetam os dados observados. Por exemplo, ao atirar uma moeda, a equidade da moeda pode ser definida como o parâmetro da moeda denotado por θ. O resultado dos eventos Pode ser denotado por D.

responda isso agora., Qual é a probabilidade de 4 cabeças em cada 9 jogadas (D) dada a equidade da moeda (θ). I. e P(D|θ)

espera, fiz a pergunta certa? Não.

devemos estar mais interessados em saber : Dado um resultado (D) qual é o probbaility de moeda que é justo (θ=0.5)

Permite representá-lo usando o Teorema de Bayes:

P(θ|D)=(P(D|θ) X P(θ))/P(D)

Aqui, P(θ) é o eu.e a força de nossa crença na justiça de moeda antes do lance., É perfeitamente normal acreditar que a moeda pode ter qualquer grau de equidade entre 0 e 1.

P(D|θ) é a probabilidade de observar o nosso resultado, dada a nossa distribuição para θ. Se soubéssemos que a moeda era justa, isso daria a probabilidade de observar o número de cabeças em um número particular de flips.

P(D) é a evidência. Esta é a probabilidade dos dados determinados pela soma (ou integração) de todos os valores possíveis de θ, ponderada por quão fortemente acreditamos nesses valores particulares de θ.,

Se tivéssemos várias visões do que é a equidade da moeda( mas não sabíamos ao certo), então isso nos diz a probabilidade de ver uma determinada sequência de flips para todas as possibilidades de nossa crença na equidade da moeda.

P(θ|D) é a crença posterior dos nossos parâmetros após observar a evidência I. e o número de cabeças.

a partir daqui, vamos mergulhar mais profundamente em implicações matemáticas deste conceito. Não te preocupes. Uma vez que você os entende, chegar a sua matemática é muito fácil.,

para definir o nosso modelo corretamente , precisamos de dois modelos matemáticos antes da mão. Um para representar a função de probabilidade P (D|θ) e o outro para representar a distribuição de crenças anteriores . O produto destes dois dá a distribuição da crença posterior P (θ|D).

uma vez que prior e posterior são ambas as crenças sobre a distribuição da equidade da moeda, a intuição diz-nos que ambos devem ter a mesma forma matemática. Lembra-te disto. Voltaremos a isso.,

assim, existem várias funções que suportam a existência do teorema de bayes. Conhecê-los é importante, por isso os expliquei em detalhes.

4.1. Bernoulli probability function

Lets recap what we learned about the likelihood function. Então, aprendemos que:

é a probabilidade de observar um número particular de cabeças em um número particular de flips para uma dada equidade de moeda. Isto significa que a nossa probabilidade de observar as cabeças/caudas depende da equidade da moeda (θ).,

P(y=1|θ)=

P(y=0|θ)=

vale a pena notar que representa 1 como chefes e 0 como caudas é apenas uma notação matemática para formular um modelo. Podemos combinar as definições matemáticas acima em uma única definição para representar a probabilidade de ambos os resultados.

P(y/θ)=

isto é chamado de função de probabilidade de Bernoulli e a tarefa de flipagem de moedas é chamada de ensaios de Bernoulli.,

y={0,1},θ=(0,1)

E, quando queremos ver uma série de chefes ou vira, sua probabilidade é dada por:

Além disso, se estamos interessados na probabilidade do número de cabeças z transformando-se em N número de flips, em seguida, a probabilidade é dada por:

4.2. Distribuição prévia de crenças

esta distribuição é usada para representar os nossos pontos fortes em crenças sobre os parâmetros baseados na experiência anterior.,mas, e se alguém não tiver experiência anterior?

não se preocupe. Matemáticos criaram métodos para mitigar este problema também. É conhecido como uninformative priors. Gostaria de o informar de antemão de que se trata apenas de um equívoco. Cada prior desinformativo sempre fornece alguma informação evento a distribuição constante prior.

Well, the mathematical function used to represent the prior beliefs is known as beta distribution., Ele tem algumas propriedades matemáticas muito boas que nos permitem modelar nossas crenças sobre uma distribuição binomial.

função de densidade de Probabilidade da distribuição beta é da forma :

onde, o nosso foco permanece no numerador. O denominador está lá apenas para garantir que a função densidade de probabilidade total após a integração avalia para 1.

α e β são chamados a forma de decidir os parâmetros da função de densidade., Aqui α é análogo ao número de cabeças nos ensaios e β corresponde ao número de caudas., O diagrama abaixo ajudará você a visualizar as distribuições beta para diferentes valores de α e β

Você também pode desenhar a distribuição beta para si mesmo usando o seguinte código na R:

Nota: α e β são intuitivos para entender, pois pode ser calculado conhecendo-se a média (µ) e desvio padrão (σ) da distribuição., Na verdade, eles estão relacionados como :

Se a média e o desvio padrão de uma distribuição são conhecidas , então não há forma de parâmetros pode ser facilmente calculado.

inferência desenhada a partir dos gráficos acima:

1. Quando não havia lançamento, acreditávamos que toda a equidade da moeda é possível como representada pela linha plana.
2. Quando havia mais o número de cabeças do que as caudas, o gráfico mostrou um pico deslocado para o lado direito, indicando maior probabilidade de cabeças e de que a moeda não é justo.,
3. à medida que Mais jogadas são feitas, e as cabeças continuam a vir em maior proporção o pico estreita a nossa confiança na equidade do valor da moeda.

4. 3. Distribuição Posterior da crença

a razão pela qual escolhemos a crença anterior é obter uma distribuição beta. Isto é porque quando a multiplicamos com uma função de probabilidade, a distribuição posterior produz uma forma semelhante à distribuição anterior que é muito mais fácil de se relacionar e entender., Se esta informação lhe abre o apetite, tenho a certeza que está pronto para andar mais um quilómetro.

vamos calcular a crença posterior usando o teorema de bayes.

o Cálculo posterior crença usando o Teorema de Bayes

Agora, o nosso posterior crença torna-se,

Isso é interessante., Apenas conhecendo a distribuição média e padrão de nossa crença sobre o parâmetro e observando o número de cabeças em n flips, podemos atualizar nossa crença sobre o parâmetro modelo().

permite entender isso com a ajuda de um exemplo simples:

suponha, você acha que uma moeda é tendenciosa. Tem um viés médio (μ) de cerca de 0,6 com desvio padrão de 0,1.

em Seguida ,

α= 13.8 β=9.2

eu.,e a nossa distribuição será tendenciosa do lado direito. Suponha, você observou 80 cabeças (z=80) em 100 flips(N=100). Vamos ver como o nosso consentimento prévio e posterior crenças estão indo olhar:

prior = P(θ|α,β)=P(θ|13.8,9.2)

Posterior = P(θ|z+α,N-z+β)=P(θ|93.8,29.2)

Permite visualizar tanto as crenças em um gráfico:

A R código para o gráfico acima é como:

}

à Medida que mais e mais flips são feitas e novos dados observados, as nossas crenças são atualizados., Este é o verdadeiro poder da Inferência Bayesiana.

Teste de Significância – Freqüentista vs Bayesiana

Sem entrar em rigorosa estruturas matemáticas, esta seção irá fornecer a você uma rápida visão geral das diferentes abordagens de freqüentista e bayesiana métodos para testar a significância e a diferença entre os grupos e que método é mais confiável.

5, 1. p-value

in this, the t-score for a particular sample from a sampling distribution of fixed size is calculated. Então, os valores p são previstos., Podemos interpretar valores p como (tomando um exemplo de valor p como 0.02 para uma distribuição da média 100) : Há 2% de probabilidade de que a amostra terá média igual a 100.

esta interpretação sofre da falha de que, para as distribuições de amostragem de diferentes tamanhos, um é obrigado a obter diferentes T-score e, portanto, diferente p-valor. É completamente absurdo. Um valor p inferior a 5% não garante que a hipótese nula esteja errada, nem um valor p superior a 5% garante que a hipótese nula esteja correta.

5.2., Intervalos de confiança

intervalos de confiança também sofrem do mesmo defeito. Além disso , como C. I não é uma distribuição de probabilidade, não há maneira de saber quais valores são mais prováveis.

5. 3. O fator Bayes

Bayes factor é o equivalente do valor p no quadro bayesiano. Vamos entendê-lo de uma forma abrangente.

The null hypothesis in bayesian framework assumes ∞ probability distribution only at a particular value of a parameter (say θ=0.5) and a zero probability else where., (M1)

a hipótese alternativa é que todos os valores de θ são possíveis, daí uma curva plana representando a distribuição. (M2)

Agora, a distribuição posterior dos novos dados parece ser a seguinte.

estatística Bayesiana ajustado credibilidade (probabilidade) de diferentes valores de θ. Pode-se ver facilmente que a distribuição de probabilidade se deslocou para o M2 com um valor superior a M1 I. E M2 é mais provável de acontecer.,

o factor Bayes não depende dos valores de distribuição reais de θ, mas da magnitude do deslocamento nos valores de M1 e M2.

no painel a (mostrado acima): barra esquerda (M1) é a probabilidade prévia da hipótese nula.

no painel B (mostrado), a barra esquerda é a probabilidade posterior da hipótese nula.

Bayes fator é definido como a razão do posterior chances para o antes desacordo;

Para rejeitar uma hipótese nula, um BF <1/10 é o preferido.,

podemos ver os benefícios imediatos do uso do fator Bayes em vez dos valores p, uma vez que eles são independentes de intenções e tamanho da amostra.

5, 4. Intervalo de alta densidade (HDI)

HDI é formado a partir da distribuição posterior após observar os novos dados. Uma vez que o IDH é uma probabilidade, o IDH 95% dá os valores 95% mais credíveis. It is also guaranteed that 95 % values will lie in this interval unlike C. i.

Notice, how the 95% HDI in prior distribution is wider than the 95% posterior distribution., Isto é porque nossa crença em IDH aumenta com a observação de novos dados.

End Notes

o objetivo deste artigo era fazer você pensar sobre o tipo diferente de filosofias estatísticas lá fora e como qualquer um deles não pode ser usado em todas as situações.

é mais do que tempo que ambas as filosofias são fundidas para mitigar os problemas do mundo real, abordando as falhas do outro., A parte II desta série focará nas técnicas de redução de dimensionalidade usando algoritmos MCMC (Markov Chain Monte Carlo). A parte III será baseada na criação de um modelo de regressão Bayesiana a partir do zero e na interpretação dos seus resultados em R. assim, antes de começar com a parte II, gostaria de ter as suas sugestões / comentários sobre este artigo.