O Teorema de Pitágoras

Uma das mais conhecidas fórmulas matemáticas é o Teorema de Pitágoras, que nos fornece a relação entre os lados de um triângulo. Um triângulo direito consiste em duas pernas e uma hipotenusa. As duas pernas se encontram em um ângulo de 90° e a hipotenusa é o lado mais longo do triângulo direito e é o lado oposto ao ângulo direito.,

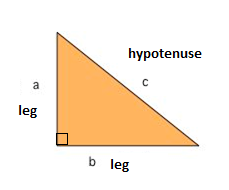
O Teorema de Pitágoras nos diz que a relação em cada triângulo é:

$$a^{2}+b^{2}=c^{2}$$

Exemplo

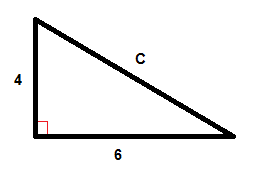
$$C^{2}=6^{2}+4^{2}$$

$$C^{2}=36+16$$

$$C^{2}=52$$

$$C=\sqrt{52}$$

$$C\approx 7.2$$

Há um par de tipos especiais de direito triângulos, como o de 45°, -45° direito de triângulos e o 30°-60° triângulo.,

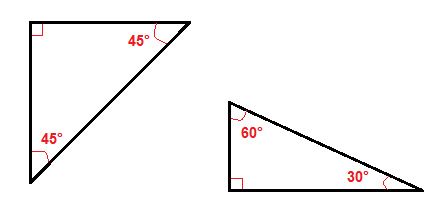
devido aos seus ângulos, é mais fácil encontrar a hipotenusa ou as pernas nestes triângulos direitos do que em todos os outros triângulos direitos.

em um triângulo de 45 ° -45° , só precisamos multiplicar uma perna por √2 para obter o comprimento da hipotenusa.

Exemplo

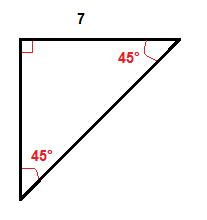
Nós multiplique o comprimento da perna, que é de 7 polegadas por √2 para obter o comprimento da hipotenusa.

$7\cdot \sqrt{2}\approx 9.,9$$

30°-60° direita, triângulo, podemos encontrar o comprimento da perna que está em frente a 30° ângulo usando esta fórmula:

$$a=\frac{1}{2}\cdot c$$

Exemplo

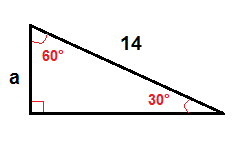
Para encontrar um, podemos usar a fórmula acima.

$$a=\frac{1}{2}\cdot 14$

$$a=7$

lição de vídeo

encontrar os lados deste triângulo direito