pressão e KMT
o fenômeno macroscópico da pressão pode ser explicado em termos da teoria molecular cinética dos gases. Assumir o caso em que uma molécula de gás (representada por uma esfera) está numa caixa, Comprimento L (Figura 1). Através do uso das suposições expostas acima, e considerando que a esfera está apenas se movendo na direção x, podemos examinar a instância da esfera colidindo elasticamente com uma das paredes da caixa.,
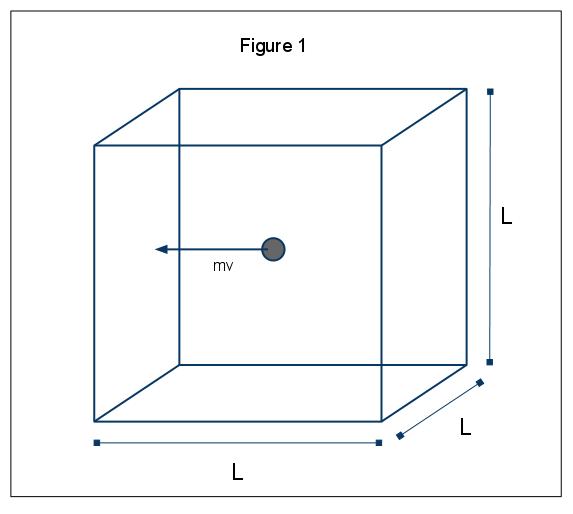
A dinâmica deste colisão é dada por p=mv, neste caso, p=mvx, uma vez que estamos apenas considerando o x dimensão. O total de dinâmica de mudança para essa colisão é dada por
\
uma vez que a quantidade de tempo que leva entre colisões da molécula com a parede é de L/vx podemos dar a freqüência de colisões da molécula contra a parede da caixa por unidade de tempo como vx/2L., Pode-se agora resolver para a mudança de momento por unidade de tempo:
\
Resolução para momento por unidade de tempo dá a força exercida por um objeto (F=ma=p/tempo)., Com a expressão que F=mvx2/L pode-se agora, calcule a pressão exercida pelo molecular de colisão, onde a área é dada como a área de uma parede de caixa, A=L2:
\
\
A expressão pode agora ser escrita em termos da pressão associada de colisões a partir de um número N de moléculas:
\
Esta expressão pode agora ser ajustado para conta para movimentação em x, y e z as direções usando quadrada média de velocidade para três dimensões e com um grande valor de N., A expressão agora é escrita como:
\
Esta expressão agora dá pressão, uma qualidade macroscópica, em termos de movimento atômico. A significância da relação acima é que a pressão é proporcional à velocidade quadrada média das moléculas em um determinado recipiente. Portanto, à medida que a velocidade molecular aumenta, também aumenta a pressão exercida sobre o recipiente.
Deixe uma resposta