|
„Bi” înseamnă „doi” (ca o bicicleta are două roți) … |
 |

Aruncarea unei Monede:
- am primit Capete (H) sau
- Cozi (T)
Noi spunem că probabilitatea de moneda de aterizare H este de ½
Și probabilitatea de moneda de aterizare T ½
hai Să dăm cu Banul.
aruncați o monedă corectă de trei ori … care este șansa de a obține două capete?,tr>












Which outcomes do we want?,
„două capete „ar putea fi în orice ordine:” HHT”,” THH „și” HTH ” toate au două capete (și o coadă). deci, 3 dintre rezultate produc „două capete”.
care este probabilitatea fiecărui rezultat?,atii sunt (P înseamnă „Probabilitatea”):
- P(Trei Capete) = P(HHH) = 1/8
- P(Două Capete) = P(HHT) + P(HTH) + P(THH) = 1/8 + 1/8 + 1/8 = 3/8
- P(Un Cap) = P(HTT) + P(THT) + P(TTH) = 1/8 + 1/8 + 1/8 = 3/8
- P(Zero Capete) = P(TTT) = 1/8
putem scrie acest lucru în termeni de o Variabilă Aleatoare, X, = „numărul de Capete din 3 aruncări ale unei monede”:
- P(X = 3) = 1/8
- P(X = 2) = 3/8
- P(X = 1) = 3/8
- P(X = 0) = 1/8
Și acest lucru este ceea ce pare ca un grafic:
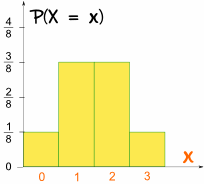
este simetric!,
A face o formulă
acum imaginați-vă că vrem șansele de 5 capete în 9 aruncări: pentru a lista toate rezultatele 512 va dura mult timp! deci, să facem o formulă.
în exemplul nostru anterior, cum putem obține valorile 1, 3, 3 și 1 ?
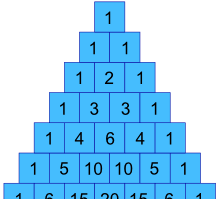
ei Bine, ele sunt, de fapt, în Triunghiul lui Pascal !
le putem face folosind o formulă?
Sigur că putem, și aici este:
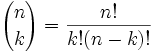
Acesta este adesea numit „n alege k”
- n = numărul total
- k = numărul vrem
- „!,”înseamnă ” factorial”, de exemplu 4! = 1×2×3×4 = 24
puteți citi mai multe despre el la combinații și permutări.
Să încercăm:
să o folosim pentru o întrebare mai dificilă:
Bias!până în prezent, șansele de succes sau eșec au fost la fel de probabile.dar ce se întâmplă dacă monedele sunt părtinitoare (teren mai mult pe o parte decât alta) sau alegerile nu sunt 50/50.
exemplu: vindeți sandvișuri. 70% dintre oameni aleg pui, restul aleg altceva.
Acest lucru este la fel ca exemplul capete și cozi, dar cu 70/30 în loc de 50/50.,
exemplu: vindeți sandvișuri. 70% dintre oameni aleg pui, restul aleg altceva.
Acest lucru este la fel ca exemplul capete și cozi, dar cu 70/30 în loc de 50/50.,
să desenăm o diagramă arbore:
cazurile „două pui” sunt evidențiate.probabilitățile pentru „doi pui” sunt de 0,147, deoarece înmulțim două 0,7 s și unul 0,3 în fiecare caz. Cu alte cuvinte
0.147 = 0.7 × 0.7 × 0.3
Sau, folosind exponenți:
= 0.72 × 0.31
0.7 este probabilitatea de fiecare alegere pe care ne-o dorim, suna-l p
2 este numărul de alegeri vrem, spunem k
Și avem (până acum):
= pk × 0.31
0.,3 este probabilitatea de alegerea opusă, astfel încât este: 1−p,
1 este numărul de vizavi de alegeri, astfel încât este: n−k
Care ne dă:
= pk(1-p)(n-k)
- p este probabilitatea de fiecare alegere pe care vrem
- k este numărul de alegeri vrem
- n este numărul total de alegeri
Acum știm că probabilitatea fiecărui rezultat este 0.147
OK. A fost multă muncă pentru ceva ce știam deja, dar acum avem o formulă pe care o putem folosi pentru întrebări mai grele.,
punerea împreună
acum știm cum să calculăm câte:
n!k!(n-k)!și probabilitatea fiecăruia:
pk(1-p) (n-k)
când se înmulțește împreună obținem:
Probabilitatea lui k din n moduri:
P(k din n) = n!k!(n-k)! pk(1-p) (n-k)
Formula probabilității binomiale generale
note importante:
- studiile sunt independente,
- există doar două rezultate posibile la fiecare studiu,
- probabilitatea de „succes” la fiecare studiu este constantă.,
Inconjunctie

Au un joc cu Inconjunctie (apoi citește Inconjunctie Explicat), pentru a vedea Distribuția Binomială în acțiune.
Arunca zarul
Un târg muri este aruncat de patru ori. Calculați probabilitățile de a obține:
- 0 Twos
- 1 Two
- 2 Twos
- 3 Twos
- 4 Twos
în acest caz n=4, p = P(două) = 1/6
X este variabila aleatorie „Numărul de Twos din patru aruncări”.,
înlocuiți x = 0 la 4 în formula:
P(k din n) = n!k!(n-k)! pk(1-p) (n-k)
astfel (la 4 zecimale):
de data aceasta graficul nu este simetric:
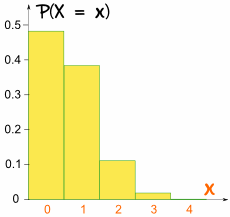
nu este simetric!este înclinat deoarece p nu este 0.5

biciclete sportive
compania dvs. face biciclete sportive. 90% trece inspecția finală (și 10% nu și trebuie să fie stabilită).
care este media și varianța preconizate pentru următoarele 4 inspecții?mai întâi, să calculăm toate probabilitățile.,
- n = 4,
- p = P ( Pass) = 0.9
X este variabila aleatoare „Numărul de treceri de la patru inspecții”.
înlocuiți x = 0 la 4 în formula:
P(k din n) = n!k!(n-k)! pk(1-p) (n-k)
media, varianța și abaterea standard
să calculăm media, varianța și abaterea Standard pentru inspecțiile bicicletelor sportive.
există formule (relativ) simple pentru ele. Ele sunt un pic cam greu de dovedit, dar ei fac munca!,
sau „valoarea așteptată”, este:
μ = np
formula Varianței este:
Varianței: σ2 = np(1-p)
Și Abaterea Standard este rădăcina pătrată a varianței:
σ = √(np(1-p))
Pentru biciclete de sport:
Varianței: σ2 = 4 × 0.9 × 0.1 = 0.36
Abaterea Standard este:
σ = √(0.36) = 0.6


Lasă un răspuns