Statistica Bayesiana a explicat pentru Începători în limba engleză Simplu

Prezentare

• dezavantaje ale frequentist statistici duce la nevoia de Statistica Bayesiana
• Descopera Statistica Bayesiana și Inferență Bayesian
• Există mai multe metode pentru a testa semnificația de model ca p-value, interval de încredere, etc

Introducere

Statistica Bayesiana continuă să rămână de neînțeles în a aprins mințile multor analiști., Fiind uimiți de puterea incredibilă a învățării automate, mulți dintre noi au devenit necredincioși față de statistici. Obiectivul nostru s-a redus la explorarea învățării automate. Nu e adevărat?

nu reușim să înțelegem că învățarea automată nu este singura modalitate de a rezolva problemele din lumea reală. În mai multe situații, nu ne ajută să rezolvăm problemele de afaceri, chiar dacă există date implicate în aceste probleme. Pentru a spune cel puțin, cunoașterea statisticilor vă va permite să lucrați la probleme analitice complexe, indiferent de dimensiunea datelor.,

în anii 1770, Thomas Bayes a introdus „Teorema lui Bayes”. Chiar și după secole mai târziu, importanța „statisticilor Bayesiene” nu a dispărut. De fapt, astăzi acest subiect este predat în profunzime în unele dintre cele mai importante universități din lume.

cu această idee, am creat acest ghid pentru începători pe Statisticile Bayesiene. Am încercat să explic conceptele într-o manieră simplistă cu exemple. Cunoașterea prealabilă a probabilității de bază & statistici este de dorit., Ar trebui să verificați acest curs pentru a obține un nivel scăzut cuprinzător privind statisticile și probabilitatea.

până la sfârșitul acestui articol, veți avea o înțelegere concretă a statisticilor Bayesiene și a conceptelor asociate acesteia.,>Teorema Bayes

Inferență Bayesian

• Bernoulli funcția probabilitate
• Înainte de Credinta Distribuție
• Posterior credința Distribuție

Test de Semnificație – Frequentist vs Bayesian

• p-value
• Intervale de Încredere
• Bayes Factor
• Densitate Mare Interval (IDU)

Înainte de a se îngropa în Statistica Bayesiana, să ne petrecem câteva minute înțelegere Frequentist Statisticilor, cea mai populara versiune de statistică, cele mai multe dintre noi au venit peste și probleme inerente în care.,

Frequentist Statistici

dezbaterea între frequentist și bayesian-au bântuit incepatori timp de secole. Prin urmare, este important să înțelegem diferența dintre cele două și cum există o linie subțire de demarcație!

este cea mai utilizată tehnică inferențială din lumea statistică. De fapt, în general, este prima școală de gândire pe care o persoană care intră în lumea statisticilor o întâlnește.

Frequentist Statistics testează dacă apare sau nu un eveniment (ipoteză)., Se calculează probabilitatea unui eveniment pe termen lung a experimentului (adică experimentul se repetă în aceleași condiții pentru a obține rezultatul).

aici, distribuțiile de eșantionare de dimensiuni fixe sunt luate. Apoi, experimentul este teoretic repetat de nenumărate ori, dar practic făcut cu o intenție de oprire. De exemplu, am efectua un experiment cu o intenție de oprire în minte că voi opri experimentul atunci când se repetă 1000 ori sau văd minim 300 capete într-o aruncare cu banul.

să mergem mai adânc acum.,

acum, vom înțelege Statisticile frequentist folosind un exemplu de aruncare a monedelor. Obiectivul este de a estima corectitudinea monedei. Mai jos este un tabel care reprezintă frecvența capetelor:

știm că probabilitatea de a obține un cap pe aruncarea unei monede corecte este 0.5. No. of heads reprezintă numărul real de capete obținute. Differenceeste diferența dintre 0.5*(No. of tosses) - no. of heads.,

Un lucru important este să rețineți că, deși diferența dintre numărul real de capete și de așteptat, numărul de capete( 50% din numărul de aruncări) crește ca număr de aruncări sunt crescute, proporția de numărul de capete la numărul total de aruncări abordări 0.5 (pentru o monedă corect).

Acest experiment ne prezintă un defect comun găsit în frequentist abordare și anume Dependența de rezultatul unui experiment privind numărul de ori experimentul se repetă.,pentru a afla mai multe despre metodele statistice frecventiste, vă puteți îndrepta către acest curs excelent privind statisticile inferențiale.

defectele inerente în Statisticile Frequentist

până aici, am văzut doar un singur defect în Statisticile frequentist. E doar începutul.

secolul 20 văzut o masivă creștere în frequentist statistică, fiind aplicate la modele numerice pentru a verifica dacă o probă este diferită de celelalte, un parametru este suficient de important pentru a fi păstrate în model și variousother manifestări de testare a ipotezei., Dar statisticile frequentist a suferit unele defecte mari în proiectarea și interpretarea sa, care a reprezentat o preocupare serioasă în toate problemele din viața reală. De exemplu:

p-values măsurată față de un eșantion (dimensiune fixă) statistica cu unele oprirea intenția schimbări cu schimbare în intenția și mărimea eșantionului. adică, dacă două persoane lucrează pe aceleași date și au o intenție de oprire diferită, pot obține două p- values diferite pentru aceleași date, ceea ce este nedorit.,

de exemplu: persoana A poate alege să nu mai arunce o monedă atunci când numărul total ajunge la 100, în timp ce B se oprește la 1000. Pentru diferite dimensiuni ale eșantionului, obținem scoruri t diferite și valori p diferite. În mod similar, intenția de a opri se poate schimba de la numărul fix de flips la Durata totală a flipping. Și în acest caz, suntem obligați să obținem valori p diferite.

2 – Interval de Încredere (C. I) ca p-value depinde foarte mult de dimensiunea eșantionului., Acest lucru face ca potențialul de oprire să fie absolut absurd, deoarece indiferent de câte persoane efectuează testele pe aceleași date, rezultatele ar trebui să fie consecvente.

3 – Intervale de Încredere (C. I) nu sunt distribuții de probabilitate, prin urmare, ele nu oferă cea mai probabilă valoare pentru un parametru și cele mai probabile valori.aceste trei motive sunt suficiente pentru a vă face să vă gândiți la dezavantajele abordării frequentiste și de ce este nevoie de abordarea bayesiană. Hai să aflăm.,de aici, vom înțelege mai întâi elementele de bază ale statisticilor Bayesiene.

Statisticile Bayesiene

” Statisticile Bayesiene sunt o procedură matematică care aplică probabilități problemelor statistice. Oferă oamenilor instrumentele necesare pentru a-și actualiza convingerile în dovezile de date noi.”

ai asta? Permiteți-mi să explic cu un exemplu:

să Presupunem că, din toate cele 4 curse de campionat (F1) dintre Niki Lauda și James hunt, Niki a câștigat de 3 ori în timp ce James a reusit doar 1.,deci, dacă ar fi să pariați pe câștigătorul următoarei curse, cine ar fi el ?pun pariu că ai spune Niki Lauda.

Iată răsucirea. Ce se întâmplă dacă vi se spune că a plouat o dată când James a câștigat și o dată când Niki a câștigat și este clar că va ploua la următoarea dată. Deci, pe cine ai paria banii acum ?

prin intuiție, este ușor de văzut că șansele de a câștiga pentru James au crescut drastic. Dar întrebarea este: cât de mult ?,

pentru a înțelege problema la îndemână, trebuie să ne familiarizăm cu unele concepte, dintre care prima este probabilitatea condiționată (explicată mai jos).în plus ,există anumite pre-rechizite:

pre-rechizite:

1. Algebra liniară : pentru a vă reîmprospăta elementele de bază, puteți consulta Algebra Academiei Khan.
2. Probabilitate și statistici de bază : pentru a vă reîmprospăta elementele de bază, puteți consulta un alt curs al Academiei Khan.

3.,1 Probabilitate Condiționată

este definită ca: Probabilitatea unui eveniment a dat B este egală cu probabilitatea de a B și-O petrece împreună împărțit la probabilitatea de B.”

De exemplu: să Presupunem două parțial intersectate seturile a și B, așa cum se arată mai jos.

setul A reprezintă un set de evenimente și setul B reprezintă altul. Dorim să calculeze probabilitatea unui anumit B sa întâmplat deja. Să reprezentăm întâmplarea evenimentului B prin umbrirea cu roșu.,

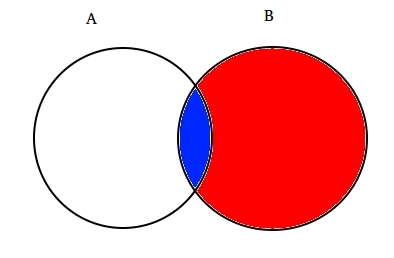
Acum, deoarece B s-a întâmplat, partea care contează acum pentru Un e partea umbrită în albastru, care este interesant . Deci, probabilitatea ca Un dat B se dovedește a fi:

prin Urmare, putem scrie formula pentru cazul B-a dat O a avut deja loc prin:

sau

Acum, cea de-a doua ecuație poate fi rescrisă ca :

Acest lucru este cunoscut sub numele de Probabilitate Condiționată.,

Să încercăm să răspundem la o problemă de pariere cu această tehnică.

Să presupunem, B fi evenimentul de a câștiga de James Hunt. O să fie evenimentul de ploaie. Prin urmare,

înlocuind valorile din formula probabilității condiționale, obținem probabilitatea de a fi în jur de 50%, ceea ce este aproape dublul de 25% când ploaia nu a fost luată în considerare (rezolvați-o la sfârșitul dvs.).

acest lucru ne-a întărit și mai mult credința că James a câștigat în lumina noilor dovezi, adică ploaie., Trebuie să vă întrebați că această formulă are o asemănare apropiată cu ceva despre care ați auzit multe. Gândește!probabil că ați ghicit corect. Pare a fi Teorema lui Bayes.Teorema Bayes este construită pe baza probabilității condiționate și se află în inima inferenței Bayesiene. Să o înțelegem în detaliu acum.

3.2 Teorema Bayes

Teorema Bayes intră în vigoare atunci când mai multe evenimente formeaza un set exhaustiv cu un alt eveniment B. Acest lucru poate fi înțeles cu ajutorul diagrama de mai jos.,

Acum, B poate fi scris ca

Deci, probabilitatea de B poate fi scris ca,

Deci, înlocuind P(B) în ecuația de probabilitate condiționată ajungem

Aceasta este ecuația de Teorema Bayes.

inferența Bayesiană

nu are rost să ne scufundăm în aspectul teoretic al acesteia. Deci, vom afla cum funcționează!, Să luăm un exemplu de aruncare a monedelor pentru a înțelege ideea din spatele inferenței bayesiene.

o parte importantă a inferenței bayesiene este stabilirea parametrilor și modelelor.

modelele sunt formularea matematică a evenimentelor observate. Parametrii sunt factorii din modelele care afectează datele observate. De exemplu, în aruncarea unei monede, corectitudinea monedei poate fi definită ca parametrul monedei notat cu θ. Rezultatul evenimentelor poate fi notat cu D.

răspundeți acum., Care este probabilitatea de 4 capete din 9 aruncări(D) având în vedere corectitudinea monedei (θ). adică P(D|θ)

așteptați, am pus întrebarea corectă? Nu.

ar trebui să fie mai interesați în a ști : a Dat un rezultat (D) care este probbaility de monedă fiind corect (θ=0.5)

vă Permite să-l reprezinte folosind Teorema Bayes:

P(θ|D)=(P(D|θ) X P(θ))/P(D)

Aici, P(θ) este înainte n-am.e puterea credinței noastre în corectitudinea de monedă înainte de aruncare., Este perfect în regulă să credem că moneda poate avea orice grad de corectitudine între 0 și 1.

P(D|θ) este probabilitatea de a observa rezultatul nostru dat de distribuție pentru θ. Dacă am știut că moneda a fost corect, acest lucru dă probabilitatea de a observa numărul de capete într-un anumit număr de flips.

P(D) este dovada. Aceasta este probabilitatea datelor determinată prin însumarea (sau integrarea) tuturor valorilor posibile ale θ, ponderată de cât de puternic credem în acele valori particulare ale θ.,

dacă am avut mai multe vizualizări despre corectitudinea monedei (dar nu știam sigur), atunci acest lucru ne spune probabilitatea de a vedea o anumită secvență de răsturnări pentru toate posibilitățile credinței noastre în corectitudinea monedei.

P(θ|D) este credința posterioară a parametrilor noștri după observarea dovezilor, adică numărul de capete.

de aici, ne vom scufunda mai adânc în implicațiile matematice ale acestui concept. Nu-ți face griji. Odată ce le înțelegeți, a ajunge la matematica sa este destul de ușor.,

pentru a defini corect modelul nostru, avem nevoie de două modele matematice înainte de mână. Una pentru a reprezenta funcția de probabilitate P (D / θ) și cealaltă pentru a reprezenta distribuția credințelor anterioare . Produsul acestor două dă credința posterioară p(θ|D) distribuție.

deoarece înainte și posterior sunt ambele credințe despre distribuția corectitudinii monedei, intuiția ne spune că ambele ar trebui să aibă aceeași formă matematică. Ține minte asta. Vom reveni la ea din nou.,

deci, există mai multe funcții care susțin existența teoremei bayes. Cunoașterea lor este importantă, de aceea le-am explicat în detaliu.

4. 1. Bernoulli funcția de probabilitate

vă permite să recapitulăm ceea ce am învățat despre funcția de probabilitate. Deci, am aflat că:

este probabilitatea de a observa un anumit număr de capete într-un anumit număr de flips pentru o anumită corectitudine de monedă. Aceasta înseamnă că probabilitatea noastră de a observa capete / cozi depinde de corectitudinea monedei (θ).,

P(y=1|θ)=

P(y=0|θ)=

de remarcat este faptul că reprezintă 1 ca șefii și 0 cozi ca este doar o notație matematică să formuleze un model. Putem combina definițiile matematice de mai sus într-o singură definiție pentru a reprezenta probabilitatea ambelor rezultate.

P(y|θ)=

Aceasta se numește Funcția Probabilitate Bernoulli și sarcina de monede flipping este numit lui Bernoulli studii.,

y={0,1},θ=(0,1)

Și, când vrem să vedem o serie de capete sau răstoarnă, probabilitatea sa este dată de:

în Plus, dacă ne interesează probabilitatea de numărul de capete z apărut în numărul N de flips atunci probabilitatea este dată de:

4.2. Prior Belief Distribution

această distribuție este utilizată pentru a reprezenta punctele noastre forte privind credințele despre parametrii bazați pe experiența anterioară.,

dar, dacă cineva nu are experiență anterioară?

nu vă faceți griji. Matematicienii au conceput metode pentru a atenua această problemă prea. Este cunoscut sub numele de uninformative priors. Aș dori să vă informez în prealabil că este doar un termen impropriu. Fiecare prior neinformativ oferă întotdeauna un eveniment Informațional distribuția constantă înainte.

ei Bine, funcții matematice utilizate pentru a reprezenta convingerile este cunoscut sub numele de beta distribution., Are câteva proprietăți matematice foarte frumoase care ne permit să ne modelăm credințele despre o distribuție binomială.funcția de densitate de probabilitate a distribuției beta este de forma:

unde, accentul nostru rămâne pe numărător. Numitorul este acolo doar pentru a se asigura că funcția de densitate totală de probabilitate la integrare evaluează la 1.

α și β sunt numite forma de a decide parametrii de funcția de densitate., Aici α este analog cu numărul de capete în studii și β corespunde numărului de cozi., Diagramele de mai jos vă va ajuta să vizualizați beta distribuții pentru diferite valori ale α și β

Nu prea pot desena beta distribuție pentru tine, folosind următorul cod în c:

Notă: α și β sunt intuitiv de înțeles, deoarece acestea pot fi calculate prin cunoașterea mediei (μ) și abaterea standard (σ) de distribuție., În fapt, ele sunt legate ca :

Daca medie și deviația standard a distribuției sunt cunoscute , atunci forma parametrii pot fi ușor calculată.

deducție trase din graficele de mai sus:

1. când nu a existat nici o aruncare am crezut că fiecare corectitudine de monede este posibilă așa cum este descris de linia plată.
2. când au existat mai multe numărul de capete decât cozile, graficul a arătat un vârf deplasat spre partea dreaptă, indicând o probabilitate mai mare de capete și că moneda nu este corect.,
3. pe măsură ce se fac mai multe aruncări, iar capetele continuă să vină în proporție mai mare, vârful se îngustează sporind încrederea noastră în corectitudinea valorii monedei.

4.3. Distribuția credinței posterioare

motivul pentru care am ales credința anterioară este obținerea unei distribuții beta. Acest lucru se datorează faptului că atunci când o înmulțim cu o funcție de probabilitate, distribuția posterioară produce o formă similară distribuției anterioare, care este mult mai ușor de relaționat și de înțeles., Dacă această mulțime de informații vă stimulează pofta de mâncare, sunt sigur că sunteți gata să mergeți o milă suplimentară.

să calculăm credința posterioară folosind teorema bayes.

Calcularea posterior credința folosind Teorema Bayes

Acum, posterior credința devine,

Acest lucru este interesant., Știind medie și standard de distribuție de credința noastră despre parametrul θ și prin observarea numărului de capete în N răstoarnă, să ne putem actualiza convingeri despre modelul parametru(θ).

să înțelegem acest lucru cu ajutorul unui exemplu simplu:

să presupunem că credeți că o monedă este părtinitoare. Are o prejudecată medie (μ) de aproximativ 0, 6 cu deviația standard de 0, 1.

Apoi ,

α= 13.8 , β=9.2

am.,distribuția noastră va fi părtinitoare pe partea dreaptă. Să presupunem, ai observat 80 de șefi (z=80) în 100 răstoarnă(N=100). Hai să vedem cum anterioară și posterioară convingeri sunt de gând să se uite:

prior = P(θ|α,β)=P(θ|13.8,9.2)

Posterior = P(θ|z+α,N-z+β)=P(θ|93.8,29.2)

vă Permite să vizualizați atât credințele pe un grafic:

R cod pentru graficul de mai sus este ca:

}

Ca mai multe și mai multe flips sunt făcute și de noi date se observă, convingerile noastre se actualizează., Aceasta este adevărata putere a inferenței Bayesiene.

Test de Semnificație – Frequentist vs Bayesian

Fără a intra în structuri matematice riguroase, această secțiune vă va oferi o privire de ansamblu rapidă de abordări diferite de frequentist și bayesian metode pentru a testa semnificația și diferența dintre grupuri și care este metoda cea mai de încredere.

5. 1. valoarea p

în acest sens, se calculează scorul t pentru un anumit eșantion dintr-o distribuție de eșantionare de dimensiune fixă. Apoi, valorile p sunt prezise., Putem interpreta valorile p ca (luând un exemplu de valoare p ca 0.02 pentru o distribuție a mediei 100) : există o probabilitate de 2% ca eșantionul să aibă medie egală cu 100.

această interpretare suferă de defectul că pentru distribuțiile de eșantionare de dimensiuni diferite, unul este obligat să obțină un scor t diferit și, prin urmare, o valoare p diferită. Este complet absurd. O valoare p mai mică de 5% nu garantează că ipoteza nulă este greșită și nici o valoare p mai mare de 5% asigură că ipoteza nulă este corectă.

5. 2., Intervale de încredere

intervalele de încredere suferă, de asemenea, de același defect. Mai mult , deoarece C. I nu este o distribuție de probabilitate, nu există nicio modalitate de a ști care valori sunt cele mai probabile.

5. 3. Bayes Factor

Bayes factor este echivalentul valorii p în cadrul bayesian. Să-l înțeleagă într-un mod cuprinzător.

ipoteza nulă din cadrul bayesian presupune distribuția probabilității ∞ numai la o anumită valoare a unui parametru (să zicem θ=0.5) și o probabilitate zero unde., (M1)

ipoteza alternativă este că toate valorile θ sunt posibile, deci o curbă plană reprezentând distribuția. (M2)

acum, distribuția posterioară a noilor date arată ca mai jos.

statistica Bayesiana ajustat credibilitatea (probabilitatea) de diferite valori ale lui θ. Se poate observa cu ușurință că distribuția probabilității sa mutat spre M2 cu o valoare mai mare decât M1, adică M2 este mai probabil să se întâmple.,

factorul Bayes nu depinde de valorile reale de distribuție ale θ, ci de magnitudinea schimbării valorilor M1 și M2.

în Panoul A( prezentat mai sus): bara stângă (M1) este probabilitatea anterioară a ipotezei nule.

în panoul B (prezentat), bara din stânga este probabilitatea posterioară a ipotezei nule.

Bayes factor este definit ca raportul dintre posterior șanse înainte de cote,

Pentru a respinge o ipoteză nulă, un BF <1/10 este de preferat.,

putem vedea beneficiile imediate ale utilizării factorului Bayes în loc de valorile p, deoarece acestea sunt independente de intenții și dimensiunea eșantionului.

5. 4. Intervalul de densitate mare (HDI)

HDI se formează din distribuția posterioară după observarea noilor date. Deoarece HDI este o probabilitate, 95% HDI dă 95% cele mai credibile valori. De asemenea, este garantat că 95 % valorile se vor afla în acest interval, spre deosebire de C. I.

Observați, cum 95% IDU în prealabil de distribuție este mai mare decât 95% posterior de distribuție., Acest lucru se datorează faptului că credința noastră în HDI crește odată cu observarea noilor date.

End Note

scopul acestui articol a fost să te gândești la alt tip de statistică filosofii acolo și cum orice singur dintre ele nu poate fi utilizat în orice situație.

este timpul ca ambele filozofii să fie îmbinate pentru a atenua problemele din lumea reală prin abordarea defectelor celuilalt., Partea a II-a a acestei serii se va concentra pe tehnicile de reducere a dimensionalității folosind algoritmi MCMC (Markov Chain Monte Carlo). Partea a III-a se va baza pe crearea unui model de regresie Bayesian de la zero și interpretarea rezultatelor sale în R. deci, înainte de a începe cu partea a II-a, aș dori să am sugestiile / feedback-ul dvs. cu privire la acest articol.