În această lecție, vom construi cele cinci (5) conectivi sau operatori logici comuni. Ele sunt considerate conexiuni logice comune, deoarece sunt foarte populare, utile și întotdeauna predate împreună.
înainte de a începe, vă sugerez să examinați cealaltă lecție în care linkul este prezentat mai jos.această lecție introductivă despre tabelele de adevăr conține cunoștințe preliminare sau informații care vă vor ajuta să înțelegeți mai bine conținutul acestei lecții.,
Introducere în Tabele de Adevăr, Declarațiile și Conective
Le prin listarea la cinci (5) comune conective logice.
Cele Cinci (5) Comune Conective Logice sau Operatorii
- Logic de Negație
- Conjuncție Logică (ȘI)
- Logică a Disjuncției (Inclusive SAU)
- Logică de Implicație (Condiționată)
- Logic Biconditional (Dublă Implicație)
I., Tabelul de adevăr al negării logice
negarea unei declarații este, de asemenea, o declarație cu o valoare de adevăr care este exact opusă celei a declarației originale. De exemplu, negarea declarația este scrisă simbolic ca
~\large{P} sau \large{\nge P}.
~{P} sau {\nge P} este citit ca „nu.”
Amintiți-vă: negarea operator notată prin simbolul ~ sau \nge ia valoarea de adevăr afirmația inițială apoi de ieșire exact opusul acestuia valoare de adevăr., Cu alte cuvinte, negarea inversează pur și simplu valoarea adevărului unei declarații date. Astfel, dacă declarația P este adevărată, atunci valoarea adevărului negării sale este falsă. În același mod, dacă P este fals, valoarea adevărului negării sale este adevărată.

II. Tabel de adevăr Logic, în Colaborare
O conjuncție este un tip de instrucțiune compusă, care este format din două propoziții (de asemenea, cunoscut ca simple afirmații) s-au alăturat de către operatorul and.,
simbolul folosit pentru a reprezenta operatorul de conjuncție AND sau logică este \ color{red} \ Large {\wedge}. Se pare ca un inversat scrisoarea V.
Dacă avem două declarații simple P și Q, și ne dorim pentru a forma o instrucțiune compusă unite prin operatorul and, putem scrie ca:
\large{P \wedge Q}.
{P \wedge Q} este citit ca „P și Q”.
Amintiți-vă: valoarea De adevăr a compus declarație P \wedge Q este adevărat numai dacă adevărul valorile P și Q sunt ambele adevărate., În caz contrar, p \wedge Q este fals.observați în tabelul de adevăr de mai jos că atunci când P este adevărat și Q este adevărat, P \wedge Q este adevărat. Cu toate acestea, celelalte trei combinații de propoziții P și Q sunt false.

III. Tabel de adevăr Logică a Disjuncției
O despărțire este un fel de instrucțiune compusă, care este compus din două propoziții simple formate prin unirea declarațiile cu SAU operator.
într-o declarație de disjuncție, utilizarea sau este inclusiv. Asta înseamnă „unul sau altul” sau ambele.,
simbolul care este folosit pentru a reprezenta operatorul de disjuncție OR sau logică este \ color{red} \ Large {\vee }. Seamănă cu litera V a alfabetului.
două propoziții P și Q Unite de către sau operator pentru a forma o declarație compusă este scrisă ca:
\large{P \Vee Q}.
{P \vee Q} este citit ca „P sau Q”.
Amintiți-vă: valoarea De adevăr a compus declarație P \vee Q este adevărată dacă valoarea de adevăr fie două declarații simple P și Q este adevărată., Moreso, P \Vee Q este adevărat și atunci când valorile adevărului ambelor afirmații P și Q sunt adevărate. Cu toate acestea, singura dată când declarația de disjuncție P \Vee Q este falsă, se întâmplă atunci când valorile adevărului atât P cât și Q sunt false.
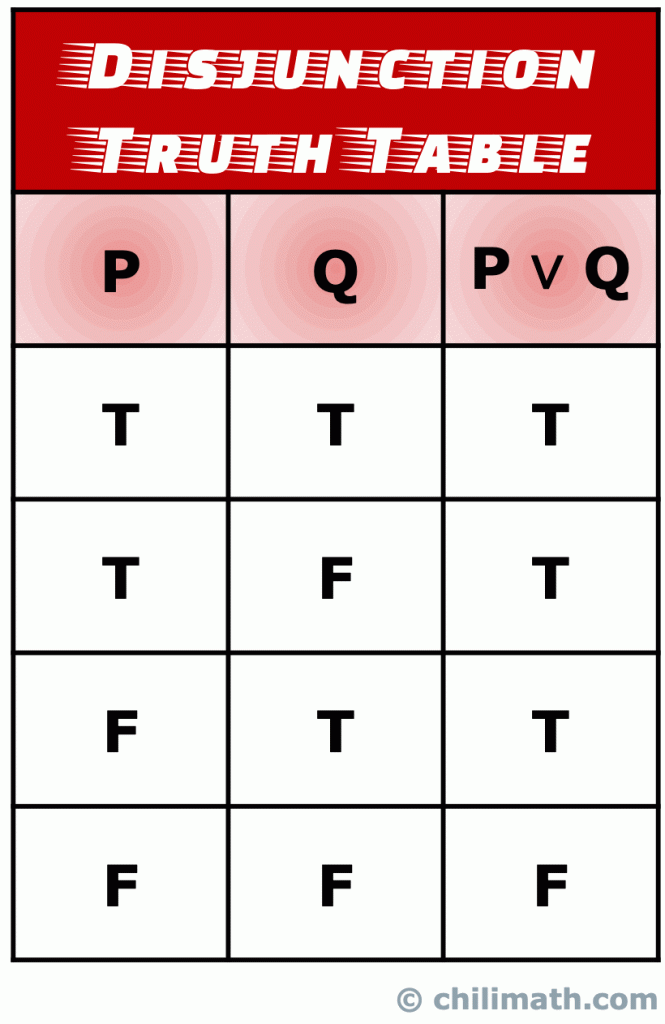
IV. Tabel de adevăr de Logică de Implicație
O implicație (de asemenea, cunoscut ca o declarație condițională) este un tip de instrucțiune compusă, care este format prin unirea a două declarații simple cu logică de implicație conjunctiv sau operator.,
simbolul folosit pentru a reprezenta operatorul implicării logice este o săgeată îndreptată spre dreapta, deci o săgeată spre dreapta.

atunci Când două declarații simple P și Q sunt unite prin implicarea operatorului, avem:
\Large{P \Q}.
- unde P este cunoscută sub numele de ipoteză
- unde Q este cunoscută sub numele de concluzie
există multe modalități de citire a condiționalului {P \to Q}., Mai jos sunt câteva dintre puținele comune.
amintiți-vă: valoarea de adevăr a instrucțiunii compuse P \to Q este adevărată atunci când ambele declarații simple P și Q sunt adevărate. Moreso, P \to Q este întotdeauna adevărat dacă P este fals. Singurul scenariu în care P \to Q este fals se întâmplă atunci când P este adevărat, iar Q este fals.
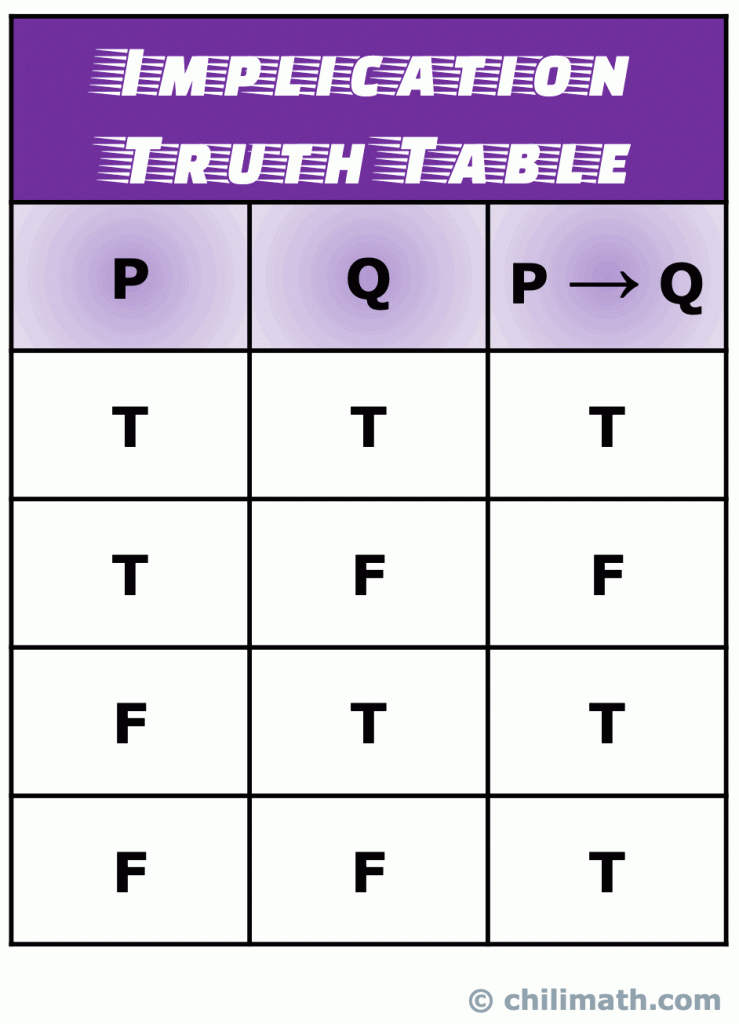
V., Tabelul de adevăr al implicării logice Bicondiționale sau duble
o implicație dublă (cunoscută și ca o declarație bicondițională) este un tip de declarație compusă care se formează prin îmbinarea a două declarații simple cu operatorul biconditional. O declarație biconditional este într-adevăr o combinație de o declarație condiționată și converse sale.operatorul bicondițional este notat cu o săgeată cu două capete.,

atunci Când vă alăturați două declarații simple (de asemenea, cunoscut sub numele moleculară declarații) cu biconditional operator, vom obține:
\Large{P \leftrightarrow Q}
{P \leftrightarrow Q} este citit ca „P dacă și numai dacă Î,”
- unde P este cunoscut ca antecedent
- unde Q este cunoscut drept consecință
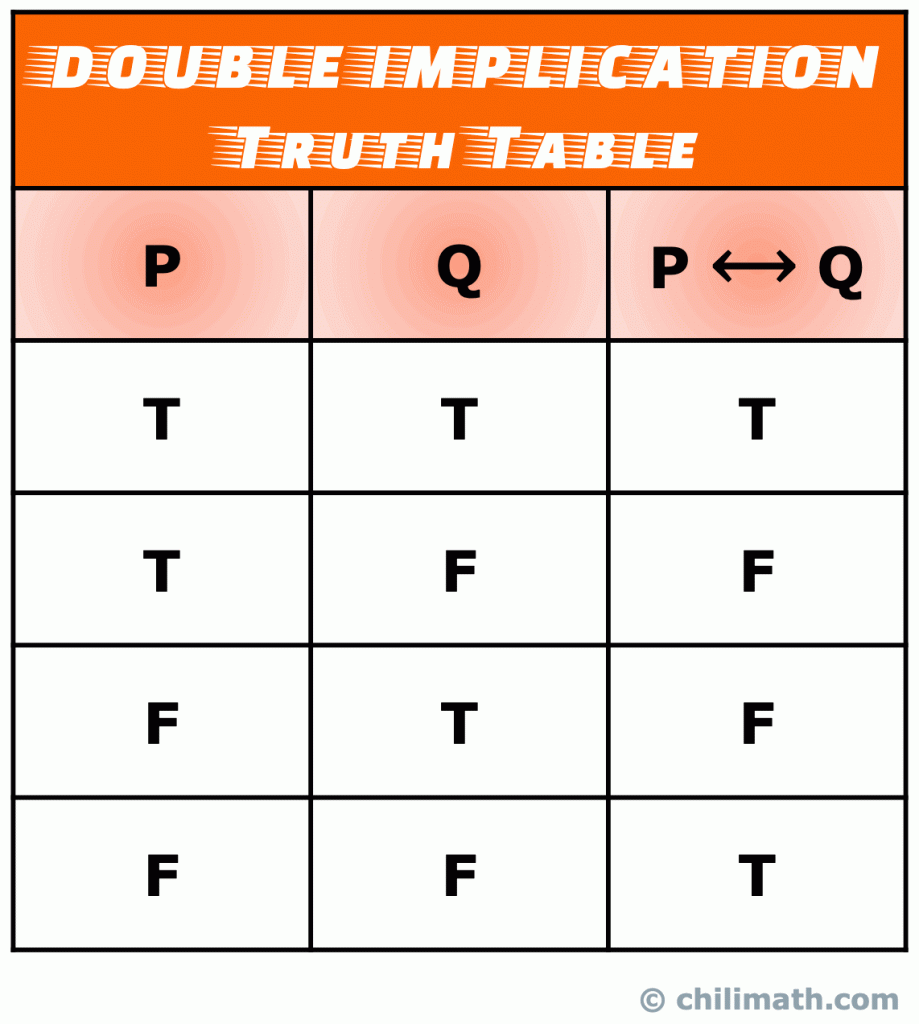
Amintiți-vă: valoarea De adevăr a biconditional declarație P \leftrightarrow Q este adevărată atunci când ambele propoziții simple P și Q sunt ambele adevărate sau ambele false. În caz contrar, P \leftrightarrow Q este fals.
s-ar putea fi, de asemenea, interesat în:
Introducere în Tabele de Adevăr, Declarațiile, și Conective Logice
Conversa, Invers, iar Contrapositive de o Declarație Condițională
Lasă un răspuns