Teorema lui Pitagora

Una dintre cele mai cunoscute formule matematice este Teorema lui Pitagora, care ne oferă relația dintre părți într-un triunghi dreptunghic. Un triunghi drept este format din două picioare și o ipotenuză. Cele două picioare se întâlnesc la un unghi de 90°, iar hypotenuse este cea mai lungă parte a triunghiului drept și este partea opusă unghiului drept.,

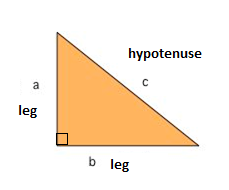
Teorema lui Pitagora ne spune că relația în fiecare triunghi dreptunghic este:

$$o^{2}+b^{2}=c^{2}$$

Exemplu

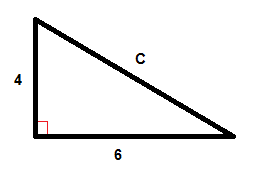
$$C^{2}=6^{2}+4^{2}$$

$$C^{2}=36+16$$

$$C^{2}=52$$

$$C=\sqrt{52}$$

$$C\aprox 7.2$$

Există o serie de tipuri speciale de triunghiuri dreapta, ca la 45°-45° la dreapta triunghiuri și 30°-60° triunghi dreptunghic.,

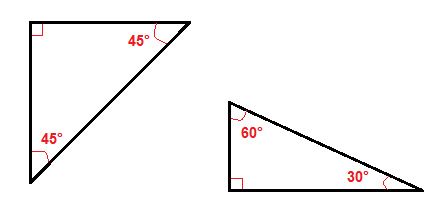
Din cauza unghiurilor lor este mai ușor să găsești hypotenuse sau picioarele în aceste triunghiuri drepte decât în toate celelalte triunghiuri drepte.într-un triunghi drept de 45°-45° trebuie doar să înmulțim un picior cu √2 pentru a obține lungimea hipotenuzei.

Exemplu

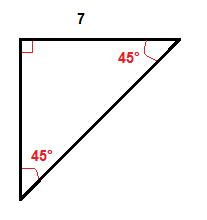
Vom multiplica lungimea piciorului care este de 7 inci cu √2 pentru a obține lungimea ipotenuzei.

$$7\cdot \ sqrt{2} \ aprox 9.,9$$

Într-un 30°-60° triunghi dreptunghic putem găsi lungimea piciorului, care este vizavi de 30° unghi de folosind această formulă:

$$a=\frac{1}{2}\cdot c$$

Exemplu

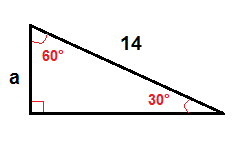
Pentru a găsi o, vom folosi formula de mai sus.

$$a=\frac{1}{2}\cdot 14$$

$$a = 7$$

lecție video

găsiți laturile acestui triunghi drept