Bayesian Statistics explained to Beginners in Simple English (Svenska)

översikt

• nackdelarna med frequentiststatistik leder till behovet av Bayesian Statistics
• Upptäck Bayesian Statistics och Bayesian Inference
• Det finns olika metoder för att testa betydelsen av modellen som p-värde, konfidensintervall, etc

introduktion

Bayesiansk statistik fortsätter att vara oförståelig i många analytikers tända sinnen., Att bli förvånad över den otroliga kraften i maskininlärning har många av oss blivit otrogen mot statistiken. Vårt fokus har minskat ner till att utforska maskininlärning. Är det inte sant?

vi förstår inte att maskininlärning inte är det enda sättet att lösa verkliga problem. I flera situationer hjälper det oss inte att lösa affärsproblem, även om det finns data som är involverade i dessa problem. Minst sagt, kunskap om statistik gör att du kan arbeta med komplexa analytiska problem, oavsett storleken på data.,

på 1770-talet introducerade Thomas Bayes ’Bayes Theorem’. Även efter århundraden senare har betydelsen av ”Bayesiansk statistik” inte bleknat bort. Faktum är att idag lärs detta ämne i stora djup i några av världens ledande universitet.

med den här idén har jag skapat den här nybörjarguiden för Bayesiansk statistik. Jag har försökt förklara begreppen på ett förenklat sätt med exempel. Förkunskaper om grundläggande Sannolikhet& statistik är önskvärd., Du bör kolla in kursen för att få en omfattande låg ner på statistik och sannolikhet.

I slutet av denna artikel kommer du att ha en konkret förståelse för Bayesiansk statistik och dess tillhörande begrepp.,Bayes teorem

Bayesian inferens

• Bernoulli Sannolikhet funktion
• tidigare tro Distribution
• Posterior tro Distribution

Test för signifikans – Frequentist vs Bayesian

• p-värde
• konfidensintervall
• Bayes faktor
• hög densitet intervall (HDI)

innan vi faktiskt gräva i Bayesiansk statistik, låt oss spendera några minuter att förstå frequentist statistik, den mer populära versionen av statistik de flesta av oss stöter på och de inneboende problemen i det.,

Frequentist statistik

debatten mellan frequentist och bayesian har hemsökt nybörjare i århundraden. Därför är det viktigt att förstå skillnaden mellan de två och hur finns det en tunn avgränsningslinje!

det är den mest använda inferentiella tekniken i den statistiska världen. Infact är i allmänhet den första tankeskolan att en person som går in i statistikvärlden stöter på.

Frequentist Statistics testar om en händelse (hypotes) inträffar eller inte., Det beräknar sannolikheten för en händelse på lång sikt av experimentet (d.v.s. experimentet upprepas under samma förhållanden för att få resultatet).

här tas samplingsfördelningarna av fast storlek. Därefter upprepas experimentet teoretiskt oändligt antal gånger men praktiskt taget gjort med en stoppintention. Till exempel utför jag ett experiment med en stopp avsikt i åtanke att jag kommer att stoppa experimentet när det upprepas 1000 gånger eller jag ser minst 300 huvuden i en myntkastning.

låt oss gå djupare nu.,

nu förstår vi frequentiststatistik med ett exempel på slantsingling. Målet är att uppskatta Myntets rättvisa. Nedan följer en tabell som representerar frekvensen av huvuden:

vi vet att sannolikheten för att få ett huvud på att kasta ett rättvist mynt är 0,5. No. of heads representerar det faktiska antalet erhållna huvuden. Difference är skillnaden mellan 0.5*(No. of tosses) - no. of heads.,

en viktig sak är att notera att även om skillnaden mellan det faktiska antalet huvuden och det förväntade antalet huvuden( 50% av antalet kasta) ökar när antalet kasta ökar, är andelen antal huvuden till det totala antalet kasta närmar sig 0,5 (för ett rättvist mynt).

detta experiment ger oss en mycket vanlig brist som finns i frequentist tillvägagångssätt, dvs beroende av resultatet av ett experiment på antalet gånger experimentet upprepas.,

för att veta mer om frequentist statistiska metoder kan du gå till denna utmärkta kurs om inferentiell statistik.

de inneboende bristerna i Frequentiststatistik

tills Här har vi bara sett en brist i frequentiststatistik. Det är bara början.

20th century såg en massiv uppgång i frekvensstatistiken som tillämpas på numeriska modeller för att kontrollera om ett prov skiljer sig från det andra, en parameter är viktig nog att hållas i modellen och olikaandra manifestationer av hypotesprovning., Men frequentist statistik lidit några stora brister i sin design och tolkning som utgjorde en allvarlig oro i alla verkliga problem. Till exempel:

p-values mätt mot ett prov (fast storlek) statistik med vissa stopp avsikt förändringar med förändring i avsikt och provstorlek. dvs. om två personer arbetar med samma data och har olika stopp avsikt, kan de få två olika p- values för samma data, vilket är oönskat.,

Till exempel: Person A kan välja att sluta kasta ett mynt när det totala antalet når 100 medan B stannar vid 1000. För olika provstorlekar får vi olika T-poäng och olika p-värden. På samma sätt kan avsikt att sluta förändras från fast antal flips till total varaktighet av flipping. Även i det här fallet måste vi få olika p-värden.

2 – konfidensintervall (C. I) somp-value beror mycket på provstorleken., Detta gör stopppotentialen helt absurd eftersom oavsett hur många personer som utför testen på samma data, bör resultaten vara konsekventa.

3 – konfidensintervall (C. I) är inte sannolikhetsfördelningar, därför ger de inte det mest sannolika värdet för en parameter och de mest sannolika värdena.

dessa tre skäl är tillräckligt för att få dig att tänka på nackdelarna med frequentist-tillvägagångssättet och varför finns det ett behov av Bayesiansk tillvägagångssätt. Låt oss ta reda på det.,

härifrån förstår vi först grunderna i Bayesiansk statistik.

Bayesiansk statistik

”Bayesiansk statistik är en matematisk procedur som tillämpar sannolikheter för statistiska problem. Det ger människor verktyg för att uppdatera sin tro i bevis på nya data.”

har du det? Låt mig förklara det med ett exempel:

Antag, av alla 4 mästerskapstävlingar (F1) mellan Niki Lauda och James hunt, Niki vann 3 gånger medan James lyckades bara 1.,

Så, om du skulle satsa på vinnaren av nästa lopp, vem skulle han vara ?

Jag slår vad om att du skulle säga Niki Lauda.

här är twist. Vad händer om du får veta att det regnade en gång när James vann och en gång när Niki vann och det är bestämt att det kommer att regna på nästa dag. Vem satsar du dina pengar på nu ?

genom intuition är det lätt att se att chanserna att vinna för James har ökat drastiskt. Men frågan är: hur mycket ?,

för att förstå problemet till hands måste vi bekanta oss med vissa begrepp, varav först är villkorlig sannolikhet (förklaras nedan).

dessutom finns det vissa förutsättningar:

förutsättningar:

1. linjär Algebra : för att uppdatera dina grunder kan du kolla in Khans Akademi Algebra.
2. sannolikhet och grundläggande statistik : för att uppdatera dina grunder kan du kolla in en annan kurs av Khan Academy.

3.,1 villkorlig sannolikhet

det definieras som: sannolikheten för en händelse A given B är lika med sannolikheten för B och en händer tillsammans dividerat med sannolikheten för B.”

till exempel: anta två delvis korsande uppsättningar A och B som visas nedan.

Set a representerar en uppsättning händelser och Set B representerar en annan. Vi vill beräkna sannolikheten för en given B har redan hänt. Låt oss representera händelsen av händelse B genom att skugga den med rött.,

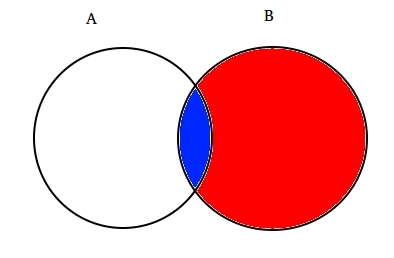
nu sedan B har hänt är den del som nu är viktig för A den del som är skuggad i blått vilket är intressant . Så, sannolikheten för en given B visar sig vara:

därför kan vi skriva formeln för Händelse B med tanke på att a redan har inträffat av:

eller

Nu kan den andra ekvationen vara skrivas om som :

detta kallas villkorlig sannolikhet.,

låt oss försöka svara på ett spelproblem med den här tekniken.

Antag, B vara händelsen att vinna av James Hunt. Ett evenemang regnar. Därför får

ersätta värdena i den villkorliga sannolikhetsformeln, vi får sannolikheten att vara runt 50%, vilket är nästan dubbelt av 25% när regn inte beaktades (lösa det i slutet).

detta stärkte vår tro på att James vann mot bakgrund av nya bevis, dvs. regn., Du måste undra att denna formel bär nära likhet med något du kanske har hört mycket om. Tänk!

förmodligen gissade du det rätt. Det ser ut som Bayes teorem.

Bayes teorem är byggd ovanpå villkorlig sannolikhet och ligger i hjärtat av Bayesian inferens. Låt oss förstå det i detalj nu.

3.2 Bayes teorem

Bayes teorem träder i kraft när flera händelser bildar en uttömmande uppsättning med en annan händelse B. Detta kan förstås med hjälp av nedanstående diagram.,

Nu kan b skrivas som

så, sannolikheten för B kan skrivas som,

men

så ersätter p(b) i ekvationen för villkorlig sannolikhet får vi

detta är ekvationen för Bayes teorem.

bayesisk inferens

det är ingen mening att dyka in i den teoretiska aspekten av den. Så vi lär oss hur det fungerar!, Låt oss ta ett exempel på myntkastning för att förstå idén bakom Bayesiansk inferens.

en viktig del av Bayesiansk inferens är upprättandet av parametrar och modeller.

modeller är den matematiska formuleringen av de observerade händelserna. Parametrar är faktorerna i modellerna som påverkar de observerade uppgifterna. Till exempel, i att kasta ett mynt, kan rättvisa av mynt definieras som parametern för mynt som betecknas med θ. Resultatet av händelserna kan betecknas med D.

svara på detta nu., Vad är sannolikheten för 4 huvuden av 9 kastar (D) med tanke på rättvisa mynt (θ). i. eP(D|θ)

vänta, ställde jag rätt fråga? Nej.

vi borde vara mer intresserade av att veta : givet ett resultat (D) vad är sannolikheten för att myntet är rättvist (θ=0.5)

Låt oss representera det med Bayes teorem:

P(θ|D)=(P(D|θ) X P(θ))/P(D)

här, P(θ) är den tidigare dvs styrkan i vår tro på myntets rättvisa före kasta., Det är helt okej att tro att mynt kan ha någon grad av rättvisa mellan 0 och 1.

P(D|θ) är sannolikheten att observera vårt resultat med tanke på vår distribution för θ. Om vi visste att myntet var rättvist, ger detta sannolikheten att observera antalet huvuden i ett visst antal flips.

P(D) är beviset. Detta är sannolikheten för data som bestäms genom att summera (eller integrera) över alla möjliga värden för θ, viktad av hur starkt vi tror på de särskilda värdena för θ.,

om vi hade flera vyer över vad Myntets rättvisa är (men visste inte säkert), så berättar det oss sannolikheten att se en viss sekvens av flips för alla möjligheter till vår tro på myntets rättvisa.

P(θ|D) är den bakre tron på våra parametrar efter att ha observerat bevisen dvs antalet huvuden.

härifrån dyker vi djupare in i matematiska konsekvenser av detta koncept. Oroa dig inte. När du förstår dem är det ganska lätt att komma till sin matematik.,

för att definiera vår modell korrekt behöver vi två matematiska modeller före handen. En som representerar sannolikhetsfunktionen P (d / θ) och den andra för att representera fördelningen av tidigare övertygelser . Produkten av dessa två ger den bakre troen p(θ|D) fördelningen.

eftersom tidigare och bakre är båda övertygelser om fördelningen av myntets rättvisa, berättar intuition att båda borde ha samma matematiska form. Kom ihåg det här. Vi kommer tillbaka till det igen.,

så det finns flera funktioner som stöder förekomsten av bayes teorem. Att känna till dem är viktigt, därför har jag förklarat dem i detalj.

4.1. Bernoulli Sannolikhet funktion

låter sammanfatta vad vi lärt oss om sannolikheten funktion. Så vi lärde oss att:

det är sannolikheten att observera ett visst antal huvuden i ett visst antal flips för en given rättvisa av mynt. Det betyder att vår sannolikhet att observera huvuden / svansar beror på myntets rättvisa (θ).,

P(y=1|θ)=

P(y=0|θ)=

det är värt att notera att representerar 1 som huvuden och 0 som svansar är bara en matematisk notation för att formulera en modell. Vi kan kombinera ovanstående matematiska definitioner i en enda definition för att representera sannolikheten för båda resultaten.

P(y/θ)=

detta kallas Bernoulli sannolikheten funktion och uppgiften att mynt vända kallas Bernoulli prövningar.,

y={0,1},θ=(0,1)

och, när vi vill se en serie huvuden eller flips, dess sannolikhet ges av:

dessutom, om du vill se en serie av huvuden eller flips, så är det troligt att:

Vi är intresserade av sannolikheten för antalet huvuden Z dyker upp i n antal flips då sannolikheten ges av:

4.2. Tidigare Trosfördelning

denna distribution används för att representera våra styrkor på övertygelser om parametrarna baserat på tidigare erfarenhet.,

men, vad händer om man inte har någon tidigare erfarenhet?

oroa dig inte. Matematiker har utarbetat metoder för att mildra detta problem också. Det är känt som uninformative priors. Jag vill i förväg informera er om att det bara är en missvisande person. Varje uninformative prior ger alltid viss information händelse konstant distribution tidigare.

Tja, den matematiska funktionen som används för att representera tidigare övertygelser kallasbeta distribution., Det har några mycket fina matematiska egenskaper som gör det möjligt för oss att modellera våra övertygelser om en binomialfördelning.

sannolikhetsdensitetsfunktionen för betadistributionen är av formen:

var ligger vårt fokus på täljare. Nämnaren är det bara för att säkerställa att den totala sannolikhetsdensitetsfunktionen vid integration utvärderar till 1.

α och β kallas parametrarna för densitetsfunktionen., Härα är analogt med antalet huvuden i försöken ochβ motsvarar antalet svansar., Diagrammen nedan hjälper dig att visualisera betadistributionerna för olika värden på α och β

Du kan också rita betadistributionen själv med följande kod i R:

notera:

id=”a7f0b721ff”> ochβ är intuitiva att förstå eftersom de kan beräknas genom att känna till medelvärdet (μ) och standardavvikelsen (σ) för distributionen., Faktum är att de är relaterade som :

om medelvärde och standardavvikelse för en distribution är kända , kan formparametrarna enkelt beräknas.

inferens dragen från grafer ovan:

1. när det inte fanns någon kasta trodde vi att varje rättvisa av mynt är möjligt som avbildas av den platta linjen.
2. när det fanns fler huvuden än svansarna visade grafen en topp skiftad mot höger sida, vilket indikerar högre sannolikhet för huvuden och det myntet är inte rättvist.,
3. eftersom fler kastar görs, och huvuden fortsätter att komma i större proportion toppen smalnar ökar vårt förtroende för rättvisan i myntvärdet.

4.3. Posterior Belief Distribution

anledningen till att vi valde tidigare tro är att få en betadistribution. Detta beror på att när vi multiplicerar det med en sannolikhetsfunktion, ger posterior distribution en form som liknar den tidigare fördelningen som är mycket lättare att relatera till och förstå., Om denna mycket information whets din aptit, jag är säker på att du är redo att gå en extra mil.

låt oss beräkna bakre tro med hjälp av bayes teorem.

beräkna posterior tro med hjälp av Bayes teorem

nu blir vår bakre tro,

det här är intressant., Bara veta medelvärdet och standardfördelningen av vår tro på parametern θoch genom att observera antalet huvuden i n flips, kan vi uppdatera vår tro på modellparametern(θ).

Låt oss förstå detta med hjälp av ett enkelt exempel:

Antag att du tror att ett mynt är partiskt. Den har en genomsnittlig (μ) bias på cirka 0.6 med standardavvikelse på 0.1.

sedan

α= 13.8 , β=9.2

I.,vår distribution kommer att vara partisk på höger sida. Antag att du observerade 80 huvuden (z=80) I 100 flips (N=100). Låt oss se hur våra tidigare och bakre övertygelser kommer att se ut:

prior = P(θ|α,β)=P(θ|13.8,9.2)

Posterior = P(θ|z+α,N-z+β)=P(θ|93.8,29.2)

låter visualisera både tron på en graf:

R-koden för ovanstående graf är som:

}

eftersom fler och fler flips görs och nya data observeras uppdateras vår tro., Detta är den verkliga kraften i Bayesiansk inferens.

Test för Betydelse – Frekventistiska vs Bayesiansk

Utan att gå in på den rigorösa matematiska strukturer, i det här avsnittet kommer att ge dig en snabb översikt av olika metoder för frekventistiska och bayesianska metoder för att testa betydelsen och skillnaden mellan grupper och vilken metod som är mest tillförlitlig.

5. 1. p-värde

I detta beräknas t-poängen för ett visst prov från en samplingsfördelning av fast storlek. Därefter förutses p-värden., Vi kan tolka p-värden som (med ett exempel på p-värde som 0,02 för en fördelning av medelvärde 100): Det finns 2% sannolikhet att provet kommer att ha medelvärde lika med 100.

denna tolkning lider av felet att för samplingsfördelningar av olika storlekar måste man få olika T-poäng och därmed olika p-värde. Det är helt absurt. Ett p-värde mindre än 5% garanterar inte att nollhypotesen är fel eller ett p-värde större än 5% säkerställer att nollhypotesen är rätt.

5. 2., Konfidensintervall

konfidensintervall lider också av samma defekt. Dessutom eftersom C. I inte är en sannolikhetsfördelning finns det inget sätt att veta vilka värden som är mest sannolika.

5. 3. Bayes Factor

Bayes factor motsvarar p-värde i Bayesianska ramverket. Låt oss förstå det på ett omfattande sätt.

nollhypotesen i bayesian framework förutsätter endast sannolikhetsfördelning med ett visst värde av en parameter (säg θ=0.5) och en noll Sannolikhet där., (M1)

den alternativa hypotesen är att alla värden på θ är möjliga, därav en platt kurva som representerar fördelningen. (M2)

nu ser den bakre fördelningen av de nya uppgifterna ut nedan.

Bayesiansk statistik justerat trovärdighet (Sannolikhet) av olika värden på θ. Det kan lätt ses att sannolikhetsfördelningen har skiftat mot M2 med ett värde högre än M1 dvs M2 är mer sannolikt att hända.,

Bayes faktor beror inte på de faktiska fördelningsvärdena för θ men storleken på skiftet i värden på M1 och M2.

i panel A (visas ovan): vänster bar (M1) är den tidigare sannolikheten för nollhypotesen.

i panel B (visas) är den vänstra baren den bakre sannolikheten för nollhypotesen.

Bayes faktor definieras som förhållandet mellan de bakre oddsen till de tidigare oddsen,

för att avvisa en nollhypotes föredras en BF<1/10.,

vi kan se de omedelbara fördelarna med att använda Bayes-faktor istället för p-värden eftersom de är oberoende av avsikter och provstorlek.

5.4. Högdensitetsintervall (HDI)

HDI bildas från den bakre fördelningen efter att ha observerat de nya data. Eftersom HDI är en sannolikhet, 95% HDI ger 95% mest trovärdiga värden. Det är också garanterat att 95% värden kommer att ligga i detta intervall till skillnad från C. I.

observera, hur 95% HDI i tidigare fördelning är bredare än 95% bakre fördelning., Detta beror på att vår tro på HDI ökar vid observation av nya data.

slutnot

syftet med den här artikeln var att få dig att tänka på olika typer av statistiska filosofier där ute och hur en enda av dem inte kan användas i alla situationer.

det är hög tid att båda filosofierna slås samman för att mildra de verkliga problemen genom att ta itu med bristerna hos den andra., Del II i denna serie kommer att fokusera på Dimensionsreduceringstekniker med hjälp av MCMC (Markov Chain Monte Carlo) algoritmer. Del III kommer att baseras på att skapa en bayesisk regressionsmodell från början och tolka dess resultat i R. så, innan jag börjar med del II, skulle jag vilja ha dina förslag / feedback på den här artikeln.