Binomialdistributionen

”Bi” betyder ”två” (som en cykel har två hjul) … … så det handlar om saker med två resultat.,

låt oss kasta ett mynt!

kasta ett rättvist mynt tre gånger … vad är chansen att få två huvuden?,tr>

THH THT TTH TTT

Which outcomes do we want?,

”två huvuden” kan vara i vilken ordning som helst: ”HHT”, ”THH” och ”HTH” har alla två huvuden (och en svans).

så 3 av resultaten ger ”två huvuden”.

vad är sannolikheten för varje resultat?,ationer är (P betyder ”Sannolikhet för”):

• p (tre huvuden) = p ( HHH) = 1/8
• p(två huvuden) = p(HHT) + p (HTH) + p (THH) = 1/8 + 1/8 + 1/8 = 3/8
• p (ett huvud) = p (HTT) + p (THT) + p (TTH) = 1/8 + 1/8 + 1/8 = 3/8
• p(noll huvuden) = p(TTT) = 1/8

Vi kan skriva detta i form av en slumpmässig variabel, X, = ”antalet huvuden från 3 kastar ett mynt”:

• P(X = 3) = 1/8
• P(X = 2) = 3/8
• P(x = 1) = 3/8
• P(X = 0) = 1/8

och det här är hur det ser ut som en graf:

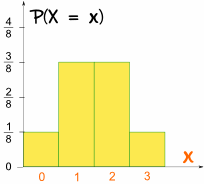
det är symmetriskt!,

att göra en formel

föreställ dig nu att vi vill ha chansen att 5 huvuden i 9 kastar: för att lista alla 512 resultat kommer att ta lång tid!

så låt oss göra en formel.

i vårt tidigare exempel, hur kan vi få värdena 1, 3, 3 och 1 ?

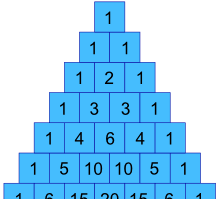
Ja, De är faktiskt i Pascals triangel !

kan vi göra dem med en formel?

visst kan vi, och här är det:

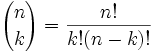
det kallas ofta ”n choose k”

• n = total number
• k = number we want
• the ”!,”betyder ” factorial”, till exempel 4! = 1×2×3×4 = 24

Du kan läsa mer om det vid kombinationer och permutationer.

låt oss prova det:

Låt oss använda det för en hårdare fråga:

Bias!

hittills har chanserna för framgång eller misslyckande varit lika troliga.

men vad händer om mynten är partiska (landa mer på ena sidan än en annan) eller val är inte 50/50.

låt oss rita ett träddiagram:

de ”två kyckling” fallen är markerade.

sannolikheten för ”två kycklingar” fungerar alla för att vara 0.147, eftersom vi multiplicerar två 0.7 s och en 0.3 i varje enskilt fall. Med andra ord

0.147 = 0.7 × 0.7 × 0.3

eller, med hjälp av exponenter:

= 0,72 × 0,31

0,7 är sannolikheten för varje val vi vill, kalla det p

2 är antalet val vi vill, kalla det k

och vi har (hittills):

= pk × 0,31

0.,3 är sannolikheten för det motsatta valet, så det är: 1−p

1 är antalet motsatta val, så det är: n−k

vilket ger oss:

= pk(1-p)(n-k)

där

• p är sannolikheten för varje val vi vill ha
• k är antalet val vi vill ha
• n är det totala antalet val vi vill ha
• n är det totala antalet val vi vill ha val

nu vet vi sannolikheten för varje resultat är 0.147

OK. Det var mycket arbete för något vi redan visste, men nu har vi en formel som vi kan använda för hårdare frågor.,

sätta ihop det

nu vet vi hur man beräknar hur många:

n!k!(n-k)!

och sannolikheten för varje:

pk(1-p) (n-k)

När multipliceras tillsammans får vi:

viktiga anmärkningar:

• försöken är oberoende,
• Det finns bara två möjliga resultat vid varje försök,
• sannolikheten för ”framgång” vid varje försök är konstant.,

Quincunx

Spela med Quincunx (läs sedan Quincunx förklarat) för att se binomialfördelningen i aktion.

kasta tärningen

en rättvis tärning kastas fyra gånger. Beräkna sannolikheterna för att få:

• 0 tvåor
• 1 två
• 2 tvåor
• 3 tvåor
• 4 tvåor

i det här fallet n=4, p = p(två) = 1/6

X är den slumpmässiga variabeln ”antal tvåor från fyra kast”.,

ersätt x = 0 till 4 i formeln:

P(k av n) = n!k!(n-k)! Pk(1-p) (n-k)

Så här (till 4 decimaler):

den här gången är grafen inte symmetrisk:

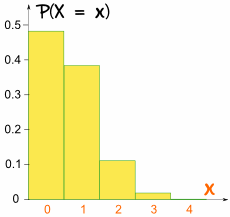
Den är inte symmetrisk!

det är skevt eftersom p inte är 0,5

sportcyklar

ditt företag gör sportcyklar. 90% passera slutlig inspektion (och 10% misslyckas och måste fastställas).

vad är det förväntade medelvärdet och variansen för de 4 Nästa inspektionerna?

låt oss först beräkna alla sannolikheter.,

• n = 4,
• p = p(Pass) = 0.9

X är den slumpmässiga variabeln ”antal pass från fyra inspektioner”.

ersätt x = 0 till 4 i formeln:

P(k av n) = n!k!(n-k)! Pk(1-p) (n-k)

medelvärde, varians och standardavvikelse

låt oss beräkna medelvärdet, variansen och standardavvikelsen för Sportcykelinspektionerna.

det finns (relativt) enkla formler för dem. De är lite svåra att bevisa, men de arbetar!,

medelvärdet, eller ”förväntat värde”, är:

μ = NP

formeln för varians är:

varians: σ2 = NP(1-p)

och standardavvikelse är kvadratroten av varians:

σ = √(NP(1-p))