Teoretisk bakgrund
innehållsförteckning
introduktion
fribärarstrålen är en av de enklaste strukturerna. Den har bara ett stöd, i en av dess ändar. Stödet är ett så kallat fast stöd som hämmar all rörelse, inklusive vertikala eller horisontella förskjutningar samt eventuella rotationer. Den andra änden är inte stöds, och därför är det gratis att flytta eller rotera. Denna fria ände kallas ofta toppen av fribäraren.,
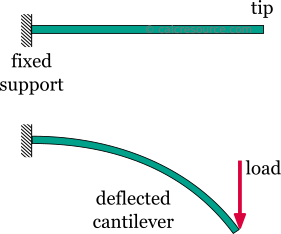
att ta bort singestödet eller sätta in ett internt gångjärn, skulle göra fribärande balken i en mekanism: en kropp rör sig utan begränsning i en eller flera riktningar. Detta är oönskad situation för en lastbärande struktur. Som ett resultat erbjuder fribärande strålen ingen redundans när det gäller stöd. Om ett lokalt fel inträffar skulle hela strukturen kollapsa., Dessa typer av strukturer, som inte erbjuder någon redundans, kallas kritiska eller determinanta strukturer. Tvärtom kallas en struktur som har fler stöd än vad som krävs för att begränsa sina fria rörelser överflödig eller obestämd struktur. Fribärande strålen är en determinant struktur.
annonsering
antaganden
den statiska analysen av varje lastbärande struktur innebär uppskattning av dess inre krafter och stunder, liksom dess avböjningar., Typiskt, för en planstruktur, med i planbelastning, är de inre åtgärderna av intresse den axiella kraften N, den tvärgående skjuvkraften V och böjningsmomentet m . För en fribärande stråle som endast bär tvärgående belastningar är axialkraften alltid noll, förutsatt att avböjningarna är små. Därför är det ganska vanligt att försumma axiella krafter.,
de beräknade resultaten på denna sida baseras på följande antaganden:
- materialet är homogent och isotropt (med andra ord dess egenskaper är desamma i någonsin punkt och mot någon riktning)
- materialet är linjärt elastiskt
- belastningarna appliceras på ett statiskt sätt (de ändras inte med tiden)
- tvärsnittet är detsamma i hela strållängden
- avböjningarna är små
- varje tvärsnitt som initialt är plan och även normal till längdaxeln, förblir plan och normal till den avböjda axeln också., Detta är fallet när tvärsnittshöjden är ganska mindre än strållängden (10 gånger eller mer) och tvärsnittet är inte flerskiktat (inte en sandwichtypssektion).
de två sista antagandena uppfyller de kinematiska kraven för Euler Bernoulli-strålteorin som antas här också.
Sign convention
för beräkning av de inre krafterna och stunderna, vid vilken sektion som helst av strålen, är en skyltkonvention nödvändig., Följande antas här:
- axialkraften anses vara positiv när den orsakar spänning till delen
- skjuvkraften är positiv när den orsakar en klockvis rotation av delen.
- böjmomentet är positivt när det orsakar spänning till strålens nedre fiber och kompression till toppfibern.
dessa regler, men inte obligatoriska, är ganska universella. En annan uppsättning regler, om de följs konsekvent skulle också ge samma fysiska resultat.,m
symboler
- e : den materiella elasticitetsmodulen (Youngs modul)
- i : tröghetsmomentet i tvärsnittet runt den elastiska neutrala böjningsaxeln
- l : den totala strållängden
- R : stödreaktion
- d : böjning
- d : böjning
- /li>
- m : böjmoment
- v : tvärgående skjuvkraft
- \theta: lutning
fribärande stråle med likformig fördelad belastning
belastningen w fördelas över fribärande span, med konstant magnitud och riktning., Dess dimensioner är kraft per längd. Den totala mängden kraft som appliceras på fribärande strålen är W=w l, där L strålens längd. Antingen den totala kraften W eller den fördelade kraften per längd w kan ges, beroende på omständigheterna.
Följande tabell innehåller formlerna som beskriver den statiska responsen hos fribärande Balk under en jämn fördelad belastning w .
annons
fribärande stråle med punktkraft vid spetsen
kraften är koncentrerad till en enda punkt, belägen vid den fria änden av strålen., I praktiken kan dock kraften spridas över ett litet område, även om dimensionerna på detta område bör vara betydligt mindre än fribärande längd. I närheten av kraftapplikationen förväntas stresskoncentrationer och som ett resultat är det svar som förutses av den klassiska strålteorin kanske felaktigt. Detta är dock bara ett lokalt fenomen. När vi rör oss bort från kraftplatsen blir resultaten giltiga, på grund av Saint-Venant-principen.,
Följande tabell innehåller formlerna som beskriver den statiska responsen hos fribärande strålen under en koncentrerad punktkraft P , införd vid spetsen.
fribärande stråle med punktkraft i ett slumpmässigt läge
kraften är koncentrerad till en enda punkt, var som helst över fribärande längd. I praktiken kan dock kraften spridas över ett litet område. För att betrakta kraften som koncentrerad bör dock applikationsområdets dimensioner vara betydligt mindre än strållängden., I närheten av kraften förväntas stresskoncentrationer och som ett resultat kan svaret som förutses av den klassiska strålteorin vara felaktigt. Detta är dock bara ett lokalt fenomen, och när vi flyttar bort från kraftplatsen blir skillnaden mellan resultaten försumbar.
Följande tabell innehåller formlerna som beskriver det statiska svaret hos fribärande strålen under en koncentrerad punktkraft P , införd på ett slumpmässigt avstånd A från det fasta stödet.,
fribärande stråle med punktmoment
i detta fall införs ett ögonblick i en enda punkt av strålen, var som helst över spännvidden. I praktiken kan det vara ett kraftpar, eller en medlem i vridning, ansluten ur planet och vinkelrätt mot strålen.
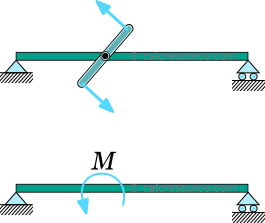
i vilket fall som helst bör applikationsområdet sprida sig till en liten längd av fribäraren, så att det framgångsrikt kan idealiseras som ett koncentrerat ögonblick till en punkt., Även om i närheten av applikationsområdet förväntas de förutsagda resultaten genom den klassiska strålteorin vara felaktiga (på grund av stresskoncentrationer och andra lokaliserade effekter), blir de förutsagda resultaten helt giltiga när vi flyttar bort, vilket anges av Saint-Venant-principen.
Följande tabell innehåller formlerna som beskriver det statiska svaret hos fribärande strålen under ett koncentrerat punktmoment M , pålagt på ett avstånd A från det fasta stödet.,
fribärande stråle med varierande fördelad belastning
lasten fördelas över fribärande längd, med linjärt varierande storlek, från w_1 vid fast stöd, till w_2 vid den fria änden. Måtten på w_1 och w_2 är kraft per längd. Den totala mängden kraft som appliceras på strålen är W = {l \ over2} (w_1 + w_2), där L fribärarlängden.
värdena för w_1 och w_2 kan tilldelas fritt. Det är inte obligatoriskt för den förstnämnda att vara mindre än den senare. De kan ta till och med negativa värden (en eller båda).,
om w_1=0 motsvarar formlerna i följande tabell en triangulär distribuerad belastning med ökande storlek (topp vid spetsen).
om w_2=0 motsvarar formlerna i följande tabell en triangulär distribuerad belastning med minskande magnitud (topp vid det fasta stödet).
Följande tabell innehåller formlerna som beskriver den statiska responsen hos fribärande Balk under en varierande fördelad belastning, av trapetsform.,
fribärande Balk med trapetsformad lastfördelning av platta typ
denna lastfördelning är typisk för fribärande balkar som stöder en platta. Fördelningen ser ut som en rätt trapezoid, med en ökande del nära det fasta stödet och en konstant del, med magnitud lika med w , vid återstående längd, upp till spetsen. Måtten på w är kraft per längd. Den totala mängden kraft som appliceras på strålen är W=w (L-a/2) , där L är fribärande längd och a är längden nära det fasta stödet, där lastfördelningen varierar (triangulär).,
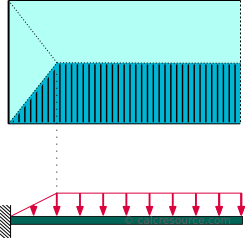
Följande tabell innehåller formlerna som beskriver den statiska responsen hos fribärande Balk under en trapezformad lastfördelning, på grund av en platta, som visas i schemat ovan.
fribärande Balk med delvis fördelad likformig belastning
lasten fördelas till en del av fribärande längd, med konstant magnitud w , medan den återstående längden lossas. Måtten på w är kraft per längd., Den totala mängden kraft som appliceras på strålen är W = w \ left (L-A-B\right) , där L fribärande längd och A , B de lossas längderna på vänster respektive höger sida av strålen, respektive.
Följande tabell innehåller formlerna som beskriver den statiska responsen hos fribärande Balk under en delvis fördelad likformig belastning.
fribärande Balk med delvis fördelad trapezformad belastning
lasten fördelas till en del av fribärande längd, med linjärt varierande storlek från w_1 till w_2 , medan den återstående längden lossas., Måtten på w_1 och w_2 är kraft per längd. Den totala mängden kraft som appliceras på strålen är W = {L-A-B\over2}(w_1+w_2) , där L strålens längd och A , B de lossade längderna på vänster respektive höger sida av strålen.
värdena för w_1 och w_2 kan tilldelas fritt. Det är inte obligatoriskt för den förstnämnda att vara mindre än den senare. De kan ta till och med negativa värden (en eller båda).
detta är det mest generiska fallet., Formlerna för delvis fördelade likformiga och triangulära belastningar kan härledas genom att på lämpligt sätt ställa in värdena för w_1 och w_2 . Dessutom kan de respektive Fallen för fullt laddad spännvidd härledas genom att ställa in a och B till noll.
Följande tabell innehåller formlerna som beskriver den statiska responsen hos fribärande Balk under en delvis fördelad trapezformad belastning.,
Lämna ett svar