en av de mest kända matematiska formlerna är Pythagoras sats, vilket ger oss förhållandet mellan sidorna i en rätt triangel. En rätt triangel består av två ben och en hypotenus. De två benen möts i 90° vinkel och hypotenusen är den längsta sidan av den högra triangeln och är sidan motsatt rätt vinkel.,
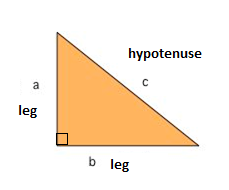
Pythagoras teorem berättar att förhållandet i varje rätt triangel är:
$$a^{2}+b^{2}=c^{2}$$
exempel
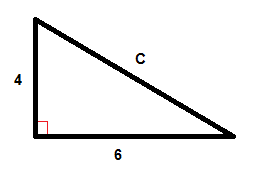
$ $ C^{2}=6^{2}+4^{2}$$
$$C^{2}=36+16$$
$$C^{2}=52$$
$$c=\sqrt{52}$$
$$c\approx 7.2$$
det finns ett par speciella typer av högra trianglar, som 45°-45° högra trianglar och 30°-60° högra triangeln.,
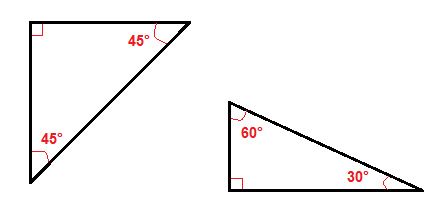
på grund av deras vinklar är det lättare att hitta hypotenusen eller benen i dessa högra trianglar än i alla andra högra trianglar.
i en 45°-45° rätt triangel behöver vi bara multiplicera ett ben med √2 för att få hypotenusens längd.
exempel
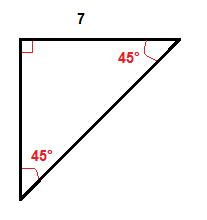
vi multiplicerar längden på benet som är 7 tum med √2 för att få längden på hypotenusen.
$$7\cdot \sqrt{2}\, ca 9.,9$$
i en 30°-60° rätt triangel kan vi hitta längden på benet som ligger mitt emot 30° – vinkeln genom att använda denna formel:
$$a=\frac{1}{2} \ cdot c$$
exempel
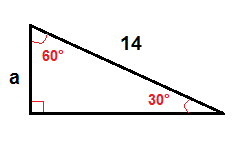
för att hitta en använder vi formeln ovan.
$$A=\frac{1}{2}\cdot 14 $ $
$$a=7 $ $
video lektion
hitta sidorna av denna högra triangel
Lämna ett svar