|
två trianglar är kongruenta om de har:
men vi behöver inte veta alla tre sidor och alla tre vinklar …vanligtvis är tre av de sex tillräckligt. |
det finns fem sätt att hitta om två trianglar är kongruenta: SSS, SAS, ASA, AAS och HL.,
SSS (sida, sida, sida)
SSS står för ”sida, sida, sida” och innebär att vi har två trianglar med alla tre sidor lika.
till exempel:
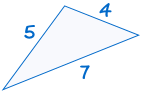 |
är kongruent till: | 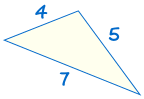 |
(se lösa SSS-trianglar för att ta reda på mer)
om tre sidor av en triangel är lika med tre sidor av en annan triangel är trianglarna kongruenta.,
SAS (sida, vinkel, sida)
SAS står för ”sida, vinkel, sida” och innebär att vi har två trianglar där vi känner till två sidor och den medföljande vinkeln är lika.,
till exempel:
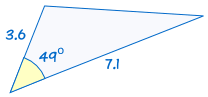 |
är kongruent till: | 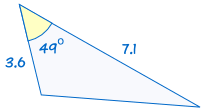 |
(se lösa SAS trianglar för att ta reda på mer)
om två sidor och den medföljande vinkeln på en triangel är lika med motsvarande sidor och vinkel på en annan triangel, är trianglarna kongruenta.,
Asa (vinkel, sida, vinkel)
Asa står för ”vinkel, sida, vinkel” och innebär att vi har två trianglar där vi vet två vinklar och den medföljande sidan är lika.,
till exempel:
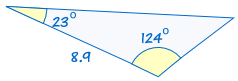 |
är kongruent till: | 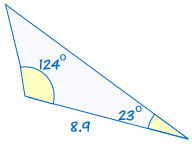 |
(se lösa Asa trianglar för att ta reda på mer)
om två vinklar och den medföljande sidan av en triangel är lika med motsvarande vinklar och sida av en annan triangel, är trianglarna kongruenta.,
AAS (vinkel, vinkel, sida)
AAS står för ”vinkel, vinkel, sida” och innebär att vi har två trianglar där vi vet två vinklar och den icke-inkluderade sidan är lika.,
till exempel:
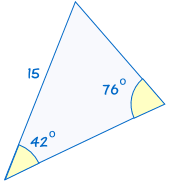 |
är kongruent till: | 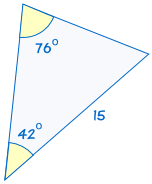 |
(se lösa AAS trianglar för att ta reda på mer)
om två vinklar och den icke-inkluderade sidan av en triangel är lika med motsvarande vinklar och sida av en annan triangel, är trianglarna kongruenta.
HL (hypotenus, ben)
den här gäller endast rätvinkliga trianglar!,
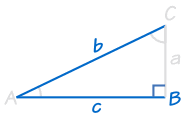 |
eller | 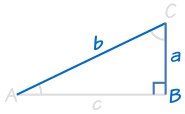 |
HL står för ”hypotenus, ben” (den längsta sidan av en rätvinklig triangel kallas ”hypotenusan”, de andra två sidorna kallas ”ben”)
det betyder att vi har två rätvinkliga trianglar med
- samma längd av hypotenus och
- samma längd för en av de andra två benen.
det spelar ingen roll vilket ben eftersom trianglarna kan roteras.,
till exempel:
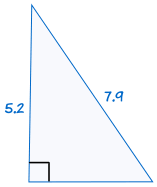 |
är kongruent till: | 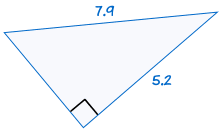 |
(se Pythagoras’ teorem för att ta reda på mer)
om hypotenusen och ett ben i en rätvinklig triangel är lika med motsvarande hypotenus och ben i en annan rätvinklig triangel är de två trianglarna kongruenta.
Varning! Använd inte ” AAA ”
AAA betyder att vi får alla tre vinklar av en triangel, men inga sidor.,
det här är inte tillräckligt med information för att avgöra om två trianglar är kongruenta!
eftersom trianglarna kan ha samma vinklar men vara olika storlekar:
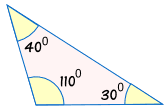 |
är inte kongruent till: | 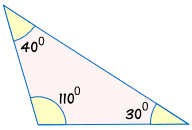 |
utan att veta minst en sida kan vi inte vara säkra på om två trianglar är kongruenta.





Lämna ett svar