i den här lektionen kommer vi att konstruera de fem (5) gemensamma logiska connectives eller operators. De anses vara vanliga logiska connectives eftersom de är mycket populära, användbara och alltid undervisade tillsammans.
innan vi börjar föreslår jag att du granskar min andra lektion där länken visas nedan.
denna inledande lektion om sanningstabeller innehåller förutsättning kunskap eller information som hjälper dig att bättre förstå innehållet i den här lektionen.,
introduktion till sanningstabeller, uttalanden och Connectives
Lens start genom att lista de fem (5) gemensamma logiska connectives.
de fem (5) gemensamma logiska Connectives eller operatorer
- logisk Negation
- logisk kombination (och)
- logisk Disjunction (inklusive eller)
- logisk implikation (villkorlig)
- logisk Bikonditionell (Dubbel implikation)
I., Sanningstabell för logisk Negation
negationen av ett uttalande är också ett uttalande med ett sanningsvärde som är exakt motsatt till det ursprungliga uttalandet. Till exempel skrivs negationen av uttalandet symboliskt som
~\large{p} eller \large{\neg p}.
~{p} eller {\neg p} läses som ”not P.”
kom ihåg: negationsoperatören betecknad med symbolen ~ eller \neg tar sanningsvärdet för det ursprungliga uttalandet och matar sedan ut exakt motsatsen till dess sanningsvärde., Med andra ord vänder negation helt enkelt sanningsvärdet av ett givet uttalande. Således, om uttalande P är sant då är sanningsvärdet av dess negation falskt. På samma sätt om P är falskt är sanningsvärdet av dess negation sant.

II. Truth Table of Logical Conjunction
en kombination är en typ av sammansatt uttalande som består av två propositioner (även känd som enkla uttalanden) Förenade av och operatör.,
symbolen som används för att representera och eller logisk sammankopplingsoperatör är \color{red}\Large{\wedge}. Det ser ut som ett inverterat brev V.
om vi har två enkla uttalanden p och Q, och vi vill bilda ett sammansatt uttalande förenat med och Operatören, kan vi skriva det som:
\large{p \wedge Q}.
{p \wedge Q} läses som ”p och Q.”
kom ihåg: sanningsvärdet för det sammansatta uttalandet p \wedge Q är bara sant om sanningsvärdena P och Q är båda sanna., Annars är p \ wedge Q falskt.
Lägg märke till i sanningstabellen nedan att när P är sant och Q är sant är p \wedge Q sant. De andra tre kombinationerna av propositioner P och Q är dock falska.

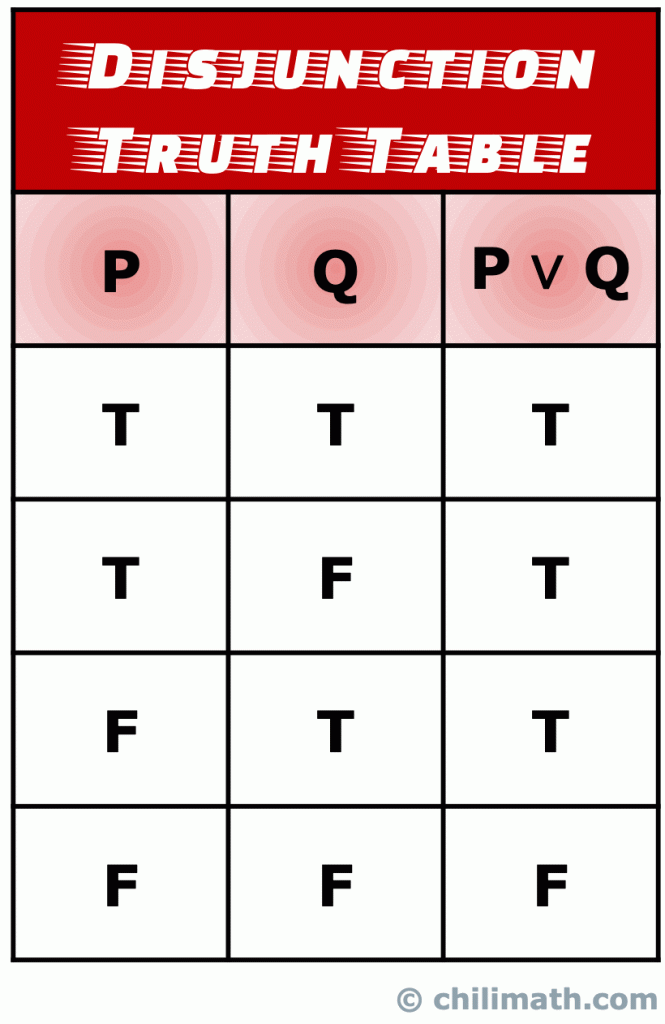
III. Truth Table of Logical Disjunction
en disjunction är ett slags sammansatt uttalande som består av två enkla uttalanden som bildas genom att gå med i uttalandena med eller operatören.
i en disjunktionsdeklaration, användningen av eller är inkluderande. Det betyder ”den ena eller den andra” eller båda.,
symbolen som används för att representera den eller logiska disjunktionsoperatören är \color{red}\Large{ \vee }. Det liknar bokstaven V i alfabetet.
två propositioner P och Q förenade med eller operatör för att bilda ett sammansatt uttalande skrivs som:
\large{p \vee Q}.
{p \vee Q} läses som ”P eller Q.”
Kom ihåg: sanningsvärdet för det sammansatta uttalandet p \vee Q är sant om sanningsvärdet för antingen de två enkla uttalandena p och Q är sant., Moreso, p \vee Q är också sant när sanningsvärdena för båda uttalandena p och Q är sanna. Men den enda gången disjunction statement p \ vee Q är falskt, händer när sanningsvärdena för både P och Q är falska.
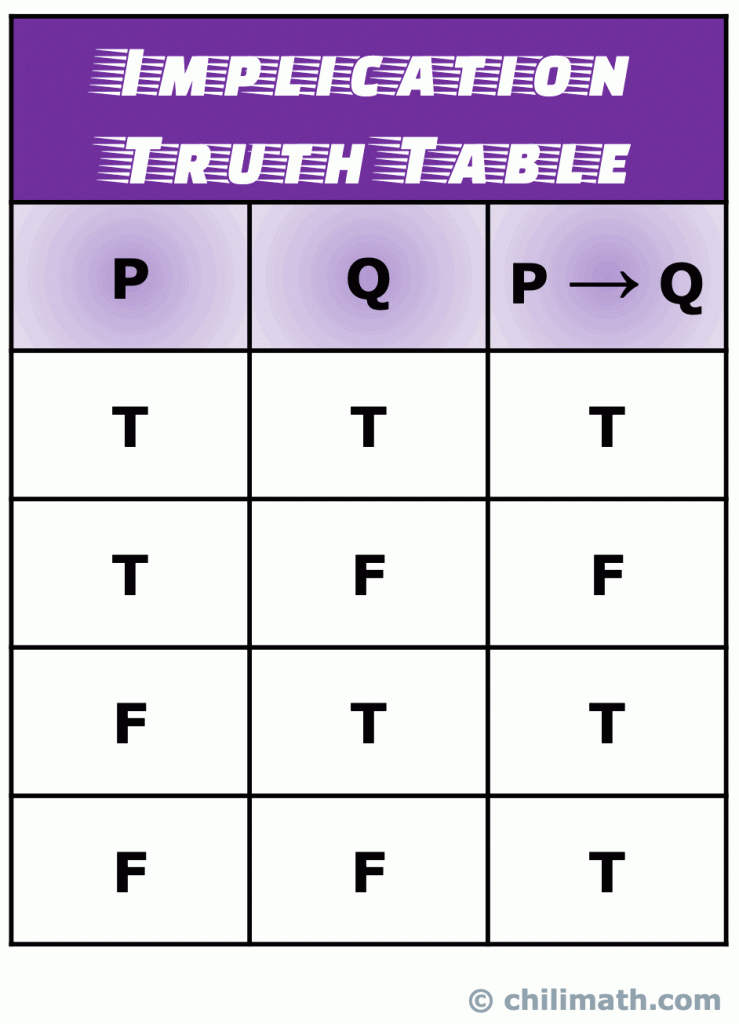
IV. Truth Table of Logical Implication
en implikation (även känd som ett villkorligt uttalande) är en typ av sammansatt uttalande som bildas genom att ansluta två enkla uttalanden med den logiska implikationen bind eller operatör.,
symbolen som används för att representera den logiska implikationsoperatören är en pil som pekar åt höger, alltså en högerpil.

När två enkla uttalanden P och Q förenas av implikationsoperatören har vi:
\Large{P \to Q}.
- där P kallas hypotesen
- där Q är känd som slutsatsen
det finns många sätt att läsa den villkorliga {p \till Q}., Nedan är några av de få vanliga.
Kom ihåg: sanningsvärdet för det sammansatta uttalandet p \ till Q är sant när både de enkla uttalandena P och Q är sanna. Moreso, p \ till Q är alltid sant om P är falskt. Det enda scenariot som p \ till Q är falskt händer när P är sant, och Q är falskt.
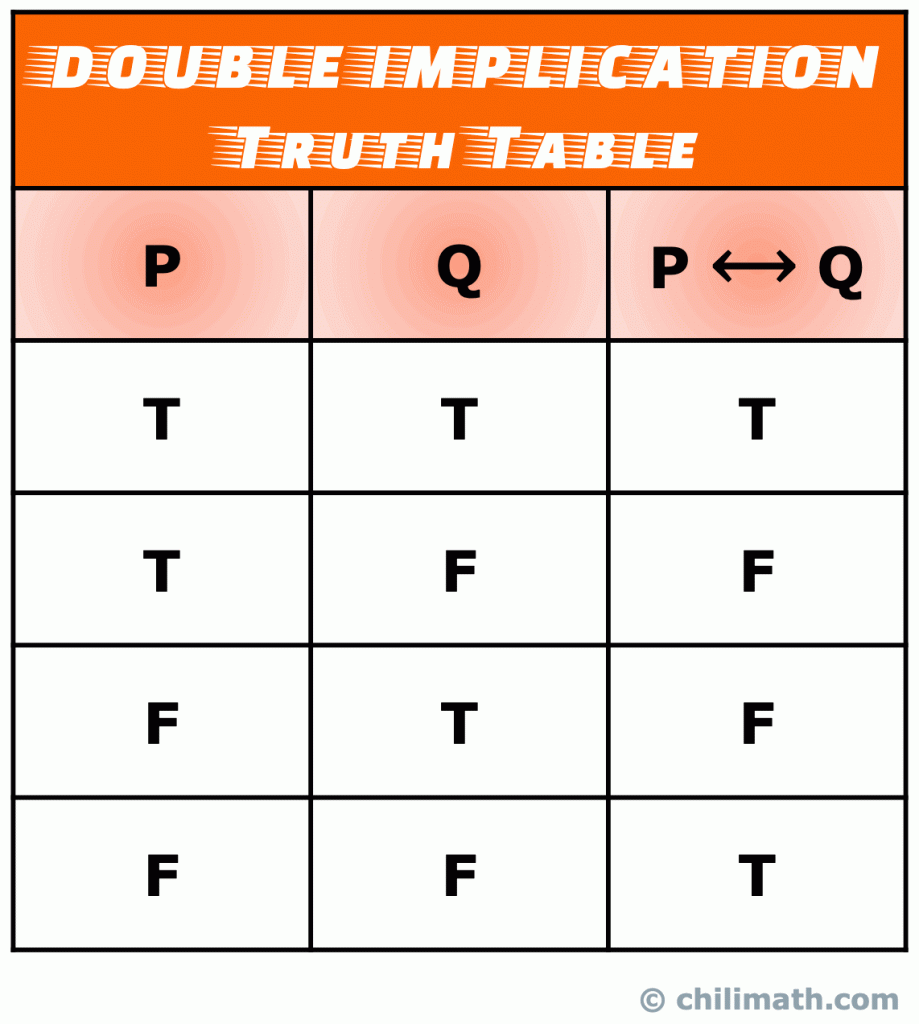
V., Truth Table of Logical Biconditional or Double Implication
en dubbel implikation (även känd som ett bikonditionellt uttalande) är en typ av sammansatt uttalande som bildas genom att gå med i två enkla uttalanden med bikonditionell operatör. Ett bikonditionellt uttalande är verkligen en kombination av ett villkorligt uttalande och dess converse.
den bikonditionella operatören betecknas med en dubbelhövdad pil.,

När du går med i två enkla uttalanden (även kända som molekylära uttalanden) med den bikonditionella operatören får vi:
\Large{p \Leftrightarrow q}
{p \Leftrightarrow q} läses som ”p om och endast om Q.,”
- där P är känd som den antecedent
- där Q är känd som den konsekventa
Kom ihåg: sanningen värdet av bikonditionella uttalande p \leftrightarrow Q är sant när både enkla uttalanden p och Q är både sanna eller båda falska. Annars är p \ leftrightarrow Q falskt.
Du kan också vara intresserad av:
introduktion till sanningstabeller, uttalanden och logiska Connectives
Converse, Inverse och Contrapositive av ett villkorligt uttalande
Lämna ett svar