Bayesian Statistics explained to Beginners in Simple English

Overview

• Die Nachteile der frequentist statistics führen zu der Notwendigkeit für Bayesian Statistics
• Entdecken Bayesian Statistics und Bayesian Inference
• Es gibt verschiedene Methoden, um die Bedeutung des Modells wie p-Wert, Konfidenzintervall, etc zu testen

Introduction

Bayes ‚ sche Statistiken bleiben in den entzündeten Köpfen vieler Analysten nach wie vor unverständlich., Erstaunt über die unglaubliche Kraft des maschinellen Lernens sind viele von uns den Statistiken untreu geworden. Unser Fokus hat sich auf die Erforschung des maschinellen Lernens beschränkt. Ist es nicht wahr?

Wir verstehen nicht, dass maschinelles Lernen nicht der einzige Weg ist, reale Probleme zu lösen. In mehreren Situationen hilft es uns nicht, Geschäftsprobleme zu lösen, obwohl Daten an diesen Problemen beteiligt sind. Gelinde gesagt, mit Kenntnis der Statistik können Sie unabhängig von der Datengröße an komplexen Analyseproblemen arbeiten.,

In den 1770er Jahren führte Thomas Bayes ‚Bayes-Theorem’ein. Auch nach Jahrhunderten später ist die Bedeutung der „Bayesischen Statistik“ nicht verblasst. Tatsächlich wird dieses Thema heute an einigen der weltweit führenden Universitäten in großer Tiefe unterrichtet.

Mit dieser Idee habe ich diesen Leitfaden für Anfänger zu Bayes-Statistiken erstellt. Ich habe versucht, die Konzepte einfach mit Beispielen zu erklären. Vorkenntnisse der Grundwahrscheinlichkeitsstatistik & sind erwünscht., Sie sollten sich diesen Kurs ansehen, um einen umfassenden Überblick über Statistiken und Wahrscheinlichkeit zu erhalten.

Am Ende dieses Artikels haben Sie ein konkretes Verständnis der Bayesschen Statistik und der damit verbundenen Konzepte.,>Bayes – Theorem

Bayessche Inferenz

• Bernoulli likelihood function
• Prior Belief Distribution
• Posterior belief Distribution

Test auf Signifikanz-Frequentist vs Bayesian

• p-Wert
• Konfidenzintervalle
• Bayes Factor
• High Density Interval (HDI)

li>

Bevor wir uns tatsächlich mit Bayesischer Statistik befassen, lassen Sie uns ein paar Minuten damit verbringen, frequentistische Statistiken zu verstehen, die populärere Version von Statistiken, auf die die meisten von uns stoßen, und die damit verbundenen Probleme.,

Frequentist Statistics

Die Debatte zwischen frequentist und bayesian verfolgt Anfänger seit Jahrhunderten. Daher ist es wichtig, den Unterschied zwischen den beiden zu verstehen und wie gibt es eine dünne Linie der Abgrenzung!

Es ist die am weitesten verbreitete inferenzielle Technik in der statistischen Welt. Tatsächlich ist es im Allgemeinen die erste Denkschule, auf die eine Person stößt, die in die Statistikwelt eintritt.

Frequentistischen Statistik tests, ob ein Ereignis (Hypothese) Auftritt oder nicht., Es berechnet die Wahrscheinlichkeit eines Ereignisses auf lange Sicht des Experiments (dh das Experiment wird unter den gleichen Bedingungen wiederholt, um das Ergebnis zu erhalten).

Hier werden die Abtastverteilungen fester Größe genommen. Dann wird das Experiment theoretisch unendlich oft wiederholt, aber praktisch mit einer Stoppabsicht durchgeführt. Zum Beispiel führe ich ein Experiment mit einer Stoppabsicht durch, um das Experiment zu stoppen, wenn es 1000 Mal wiederholt wird, oder ich sehe mindestens 300 Köpfe in einem Münzwurf.

Lass uns jetzt tiefer gehen.,

Jetzt werden wir frequentistische Statistiken anhand eines Beispiels für Münzwurf verstehen. Ziel ist es, die Fairness der Münze abzuschätzen. Unten ist eine Tabelle, die die Häufigkeit der Köpfe darstellt:

Wir wissen, dass die Wahrscheinlichkeit, eine faire Münze zu werfen, 0,5 ist. No. of heads repräsentiert die tatsächliche Anzahl der erhaltenen Köpfe. Difference ist der Unterschied zwischen 0.5*(No. of tosses) - no. of heads.,

Wichtig ist, dass der Unterschied zwischen der tatsächlichen Anzahl der Köpfe und der erwarteten Anzahl der Köpfe( 50% der Anzahl der Würfe) zunimmt, wenn die Anzahl der Würfe erhöht wird, Der Anteil der Anzahl der Köpfe an der Gesamtzahl der Würfe nähert sich 0,5 (für eine faire Münze).

Dieses Experiment zeigt uns einen sehr häufigen Fehler im frequentistischen Ansatz, dh Abhängigkeit des Ergebnisses eines Experiments von der Häufigkeit, mit der das Experiment wiederholt wird.,

Um mehr über frequentistische statistische Methoden zu erfahren, können Sie diesen hervorragenden Kurs über inferentielle Statistiken besuchen.

Die Inhärente Mängel in der Frequentistischen Statistik

Bis hier haben wir gesehen, dass nur ein Fehler in der frequentistischen Statistik. Nun, es ist nur der Anfang.

20th century saw a massive upsurge in der frequentistischen Statistik wird angewendet, um numerische Modelle zu prüfen, ob eine Probe unterscheidet sich von den anderen, ein parameter ist wichtig genug gehalten werden, in das Modell und variousother Manifestationen von Hypothese zu testen., Aber frequentistische Statistiken erlitten einige große Mängel in der Gestaltung und Interpretation, die ein ernstes Problem in allen realen Problemen warf. Beispiel:

p-values gemessen anhand einer Stichprobenstatistik (feste Größe) mit einigen Änderungen der Stoppabsicht mit Änderung der Absicht und der Stichprobengröße. dh wenn zwei Personen an denselben Daten arbeiten und unterschiedliche Stoppabsichten haben, erhalten sie möglicherweise zwei verschiedene p- values für dieselben Daten, was unerwünscht ist.,

Zum Beispiel: Person A kann wählen, eine Münze nicht mehr zu werfen, wenn die Gesamtzahl 100 erreicht, während B bei 1000 anhält. Für verschiedene Stichprobengrößen erhalten wir unterschiedliche T-Werte und unterschiedliche p-Werte. In ähnlicher Weise kann sich die Stoppabsicht von der festen Anzahl der Flips zur Gesamtdauer des Flippens ändern. Auch in diesem Fall müssen wir unterschiedliche p-Werte erhalten.

2 – Konfidenzintervall (C. I) wie p-value hängt stark von der Stichprobengröße., Dies macht das Stopppotential absolut absurd, da unabhängig davon, wie viele Personen die Tests an denselben Daten durchführen, die Ergebnisse konsistent sein sollten.

3 – Konfidenzintervalle (C. I) sind keine Wahrscheinlichkeitsverteilungen, daher liefern sie nicht den wahrscheinlichsten Wert für einen Parameter und die wahrscheinlichsten Werte.

Diese drei Gründe reichen aus, um Sie dazu zu bringen, über die Nachteile des frequentistischen Ansatzes nachzudenken und warum ein bayesischer Ansatz erforderlich ist. Lass es uns herausfinden.,

Von hier aus werden wir zunächst die Grundlagen der bayesischen Statistik verstehen.

Bayes-Statistik

„Bayes-Statistik ist ein mathematisches Verfahren, das Wahrscheinlichkeiten zu statistischen Probleme. Es bietet den Menschen die Werkzeuge, um ihre Überzeugungen in den Nachweis neuer Daten zu aktualisieren.“

hast Du das verstanden? Lassen Sie es mich mit einem Beispiel erklären:

Angenommen, von allen 4 Meisterschaftsrennen (F1) zwischen Niki Lauda und James Hunt gewann Niki 3 Mal, während James nur 1 schaffte.,

Wenn Sie also auf den Gewinner des nächsten Rennens wetten würden, wer wäre er ?

Ich wette, du würdest Niki Lauda sagen.

Hier ist der twist. Was ist, wenn Ihnen gesagt wird, dass es einmal geregnet hat, als James gewonnen hat und einmal, als Niki gewonnen hat, und es ist definitiv, dass es am nächsten Tag regnen wird. Also, auf wen würdest du jetzt dein Geld wetten ?

Durch Intuition ist es leicht zu erkennen, dass die Gewinnchancen für James drastisch gestiegen sind. Aber die Frage ist: wie viel ?,

Um das vorliegende Problem zu verstehen, müssen wir uns mit einigen Konzepten vertraut machen, zuallererst bedingte Wahrscheinlichkeit (unten erklärt).

Darüber hinaus gibt es bestimmte Voraussetzungen:

Voraussetzungen:

1. Lineare Algebra : Um Ihre Grundlagen zu aktualisieren, können Sie Khans Akademie Algebra überprüfen.
2. Wahrscheinlichkeit und grundlegende Statistiken: Um Ihre Grundlagen aufzufrischen, können Sie sich einen weiteren Kurs der Khan Academy ansehen.

3.,1 Bedingte Wahrscheinlichkeit

Es ist definiert als die: Wahrscheinlichkeit eines ereignisses A gegeben B gleich die wahrscheinlichkeit von B und A geschieht zusammen geteilt durch die wahrscheinlichkeit von B.“

Zum beispiel: Nehmen zwei teilweise schneiden mengen A und B wie unten gezeigt.

Set A repräsentiert einen Satz von Ereignissen und Set B repräsentiert einen anderen. Wir möchten die Wahrscheinlichkeit berechnen, dass ein gegebenes B bereits passiert ist. Stellen wir das Geschehen von Ereignis B dar, indem wir es mit Rot schattieren.,

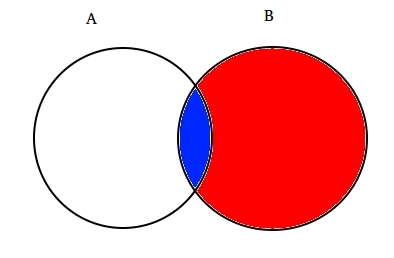
Seit B passiert ist, ist der Teil, der jetzt für A wichtig ist, der blau schattierte Teil, der interessanterweise ist. Die Wahrscheinlichkeit eines gegebenen B ist also:

Daher können wir die Formel für das Ereignis B schreiben gegeben A ist bereits aufgetreten durch:

oder

Jetzt ist die zweite Gleichung kann wie folgt umgeschrieben werden :

Dies wird als bedingte Wahrscheinlichkeit bezeichnet.,

Versuchen wir, ein Wettproblem mit dieser Technik zu beantworten.

Angenommen, B das Ereignis des Gewinnens von James Hunt sein. A sei das Ereignis des Regens. Daher

Wenn wir die Werte in der bedingten Wahrscheinlichkeitsformel ersetzen, liegt die Wahrscheinlichkeit bei etwa 50%, was fast dem Doppelten von 25% entspricht Regen wurde nicht berücksichtigt (Lösen Sie es an Ihrem Ende).

Dies stärkte unseren Glauben, dass James im Lichte neuer Beweise gewinnen würde, dh Regen., Sie müssen sich fragen, dass diese Formel eine große Ähnlichkeit mit etwas aufweist, von dem Sie vielleicht viel gehört haben. Denke!

Wahrscheinlich haben Sie es richtig erraten. Es sieht aus wie Bayes-Theorem.

Der Bayes-Satz basiert auf der bedingten Wahrscheinlichkeit und liegt im Herzen der bayesischen Inferenz. Lassen Sie uns es jetzt im Detail verstehen.

3.2 Bayes-Satz

Bayes-Satz tritt in Kraft, wenn mehrere Ereignisse eine erschöpfende Menge mit einem anderen Ereignis B bilden.,

Nun kann B geschrieben werden als

So, wahrscheinlichkeit von B geschrieben werden kann als,

Aber

Wenn wir also P(B) in der Gleichung der bedingten Wahrscheinlichkeit ersetzen, erhalten wir

Dies ist die Gleichung des Bayes-Theorems.

Bayessche Inferenz

Es hat keinen Sinn, in den theoretischen Aspekt einzutauchen. Also, wir werden lernen, wie es funktioniert!, Nehmen wir ein Beispiel für Münzwurf, um die Idee hinter Bayes ‚ scher Inferenz zu verstehen.

Ein wichtiger Teil der bayesischen Inferenz ist die Etablierung von Parametern und Modellen.

Modelle sind die mathematische Formulierung der beobachteten Ereignisse. Parameter sind die Faktoren in den Modellen, die die beobachteten Daten beeinflussen. Zum Beispiel kann beim Werfen einer Münze die Fairness der Münze als der Parameter der Münze definiert werden, der mit θ bezeichnet wird. Das Ergebnis der Ereignisse kann mit D bezeichnet werden

Beantworte dies jetzt., Wie hoch ist die Wahrscheinlichkeit von 4 Köpfen von 9 Würfen(D) angesichts der Fairness der Münze (θ)? dh P(D|θ)

Warte, habe ich die richtige Frage gestellt? Nein.

Wir sollten mehr daran interessiert sein zu wissen : Angesichts eines Ergebnisses (D), wie wahrscheinlich es ist, dass Münzen fair sind (θ=0,5)

Stellen Wir es mit Bayes-Theorem dar:

P(θ|D)=(P(D|θ) X P(θ))/P(D)

Hier P(θ) ist der Prior, dh die Stärke unseres Glaubens an die Fairness der Münze vor dem Wurf., Es ist völlig in Ordnung zu glauben, dass Münzen zwischen 0 und 1 ein beliebiges Maß an Fairness haben können.

P(D|θ) ist die Wahrscheinlichkeit, unser Ergebnis angesichts unserer Verteilung für θ zu beobachten. Wenn wir wüssten, dass Münze fair war, gibt dies die Wahrscheinlichkeit der Beobachtung der Anzahl der Köpfe in einer bestimmten Anzahl von Flips.

P(D) ist der Beweis. Dies ist die Wahrscheinlichkeit von Daten, die durch Summieren (oder Integrieren) aller möglichen Werte von θ bestimmt wird, gewichtet dadurch, wie stark wir an diese bestimmten Werte von θ glauben.,

Wenn wir mehrere Ansichten darüber hatten, was die Fairness der Münze ist (aber nicht sicher wussten), dann sagt uns dies die Wahrscheinlichkeit, eine bestimmte Folge von Flips für alle Möglichkeiten unseres Glaubens an die Fairness der Münze zu sehen.

P(θ|D) ist der hintere Glaube unserer Parameter nach Beobachtung der Beweise, dh der Anzahl der Köpfe.

von hier Aus werden wir tiefer in die mathematischen Implikationen dieses Konzepts. Keine Sorge. Sobald Sie sie verstanden haben, ist es ziemlich einfach, zu seiner Mathematik zu gelangen.,

Um unser Modell korrekt zu definieren , benötigen wir zwei mathematische Modelle vor der Hand. Eine zur Darstellung der Wahrscheinlichkeitsfunktion P(D|θ) und die andere zur Darstellung der Verteilung früherer Überzeugungen . Das Produkt dieser beiden ergibt die posteriore Verteilung P(θ|D).

Da prior und posterior beide Überzeugungen über die Verteilung der Fairness der Münze sind, sagt uns die Intuition, dass beide die gleiche mathematische Form haben sollten. Denken Sie daran. Wir werden wieder darauf zurückkommen.,

Es gibt also mehrere Funktionen, die die Existenz des Bayes-Theorems unterstützen. Sie zu kennen ist wichtig, daher habe ich sie ausführlich erklärt.

4.1. Bernoulli-likelihood-Funktion

Ermöglicht die Zusammenfassung was haben wir gelernt, über die likelihood-Funktion. So haben wir gelernt, dass:

Es ist die Wahrscheinlichkeit, eine bestimmte Anzahl von Köpfen in einer bestimmten Anzahl von Flips für eine bestimmte Fairness der Münze zu beobachten. Dies bedeutet, dass unsere Wahrscheinlichkeit, Kopf/Zahl zu beobachten, von der Fairness der Münze abhängt (θ).,

P(y=1|θ)=

P(y=0|θ)=

Es ist erwähnenswert, dass die Darstellung von 1 als Kopf und 0 als Zahl nur eine mathematische Notation ist, um ein Modell zu formulieren. Wir können die obigen mathematischen Definitionen in einer einzigen Definition kombinieren, um die Wahrscheinlichkeit beider Ergebnisse darzustellen.

P(y|θ)=

Dies nennt man den Bernoulli-Likelihood-Funktion und die Aufgabe der Münze flipping heißt Bernoulli-versuche.,

y={0,1},θ=(0,1)

Und wenn wir eine Reihe von Köpfen oder Flips sehen möchten, ist die Wahrscheinlichkeit gegeben durch:

Wenn wir interessiert an der Wahrscheinlichkeit, dass die Anzahl der Köpfe z in N Anzahl der Flips auftaucht, dann ist die Wahrscheinlichkeit gegeben durch:

4.2. Prior Belief Distribution

Diese Verteilung wird verwendet, um unsere Stärken auf Überzeugungen über die Parameter basierend auf den bisherigen Erfahrungen darzustellen.,

Aber was ist, wenn man keine Vorkenntnisse hat?

Keine Sorge. Mathematiker haben Methoden entwickelt, um dieses Problem zu mildern. Es ist bekannt als uninformative priors. Ich möchte Sie vorher darüber informieren, dass es sich nur um eine falsche Bezeichnung handelt. Jeder uninformative Prior liefert immer einige Informationen über die konstante Verteilung prior.

Nun, die mathematische Funktion zur Darstellung der vorherigen Überzeugungen ist als beta distributionbekannt., Es hat einige sehr schöne mathematische Eigenschaften, die es uns ermöglichen, unsere Überzeugungen über eine Binomialverteilung zu modellieren.

Die Wahrscheinlichkeitsdichtefunktion der Beta-Verteilung hat folgende Form:

wobei unser Fokus weiterhin auf dem Zähler liegt. Der Nenner ist nur da, um sicherzustellen, dass die Gesamtwahrscheinlichkeitsdichtefunktion bei der Integration 1 ergibt.

α und β heißen die formentscheidenden Parameter der Dichtefunktion., Hier ist α analog zur Anzahl der Köpfe in den Versuchen und β entspricht der Anzahl der Schwänze., Die folgenden Diagramme helfen Ihnen, die Beta-Verteilungen für verschiedene Werte von α und β

Auch Sie können die Beta-Verteilung mit dem folgenden Code in R selbst zeichnen:

Hinweis: α und β sind intuitiv zu verstehen, da sie durch Kenntnis des Mittelwerts (μ) und der Standardabweichung (σ) der Verteilung berechnet werden können., Tatsächlich sind sie verwandt mit:

Wenn Mittelwert und Standardabweichung einer Verteilung bekannt sind , können dort Formparameter leicht berechnet werden.

Schlussfolgerung aus den obigen Grafiken:

1. Wenn es keinen Wurf gab, glaubten wir, dass jede Fairness der Münze möglich ist, wie durch die flache Linie dargestellt.
2. Wenn mehr Köpfe als die Schwänze vorhanden waren, zeigte das Diagramm eine Spitze, die nach rechts verschoben war, was auf eine höhere Wahrscheinlichkeit von Köpfen hinweist und diese Münze ist nicht fair.,
3. Wenn mehr Würfe ausgeführt werden und die Köpfe weiterhin in einem größeren Verhältnis stehen, verengt sich der Peak und erhöht unser Vertrauen in die Fairness des Münzwert.

4.3. Posterior Belief Distribution

Der Grund, warum wir prior belief gewählt haben, besteht darin, eine Beta-Distribution zu erhalten. Dies liegt daran, dass, wenn wir es mit einer Wahrscheinlichkeitsfunktion multiplizieren, Die posteriore Verteilung eine Form ähnlich der vorherigen Verteilung ergibt, die viel einfacher zu beziehen und zu verstehen ist., Wenn so viele Informationen Ihren Appetit anregen, sind Sie sicher bereit, eine zusätzliche Meile zu gehen.

Berechnen wir den hinteren Glauben mit dem Bayes-Theorem.

Berechnung des hinteren Glaubens mit Bayes-Theorem

Jetzt wird unser hinterer Glaube

Das ist interessant., Wenn wir nur den Mittelwert und die Standardverteilung unseres Glaubens an den Parameter θ kennen und die Anzahl der Köpfe in N Flips beobachten, können wir unseren Glauben an den Modellparameter aktualisieren(θ).

Lassen Sie uns dies anhand eines einfachen Beispiels verstehen:

Angenommen, Sie denken, dass eine Münze voreingenommen ist. Es hat eine mittlere (μ) Vorspannung von etwa 0,6 mit Standardabweichung von 0,1.

Dann

α= 13.8 , β=9.2

ich.,e unsere Verteilung wird auf der rechten Seite voreingenommen sein. Angenommen, Sie beobachtet 80 Köpfe (z=80) in 100 flips(N=100). Mal sehen, wie unsere vorherigen und hinteren Überzeugungen aussehen werden:

prior = P(θ|α,β)=P(θ|13.8,9.2)

Posterior = P(θ|z+α,N-z+β)=P(θ|93.8,29.2)

Lassen Sie beide Überzeugungen in einem Diagramm visualisieren:

Der R-Code für das obige Diagramm lautet wie folgt:

}

Da immer mehr Flips gemacht werden und neue Daten beobachtet werden, werden unsere Überzeugungen aktualisiert., Dies ist die wahre Kraft der bayesschen Inferenz.

Test for Significance-Frequentist vs Bayesian

Ohne auf die strengen mathematischen Strukturen einzugehen, bietet Ihnen dieser Abschnitt einen schnellen Überblick über verschiedene Ansätze frequentistischer und bayesischer Methoden, um auf Signifikanz und Differenz zwischen Gruppen zu testen und welche Methode am zuverlässigsten ist.

5.1. p-Wert

Dabei wird der t-Score für eine bestimmte Stichprobe aus einer Stichprobenverteilung fester Größe berechnet. Dann werden p-Werte vorhergesagt., Wir können p-Werte wie interpretieren (am Beispiel des p-Wertes als 0,02 für eine Verteilung von Mittelwert 100) : Es besteht eine Wahrscheinlichkeit von 2%, dass die Stichprobe einen Mittelwert von 100 hat.

Diese Interpretation leidet unter dem Fehler, dass man bei Abtastverteilungen unterschiedlicher Größe einen unterschiedlichen t-Score und damit einen unterschiedlichen p-Wert erhalten muss. Es ist völlig absurd. Ein p-Wert von weniger als 5% garantiert nicht, dass die Nullhypothese falsch ist, und ein p-Wert von mehr als 5% stellt sicher, dass die Nullhypothese richtig ist.

5.2., Konfidenzintervalle

Konfidenzintervalle leiden ebenfalls unter demselben Defekt. Da C. I keine Wahrscheinlichkeitsverteilung ist , gibt es keine Möglichkeit zu wissen, welche Werte am wahrscheinlichsten sind.

5.3. Bayes-Faktor

Bayes-Faktor entspricht dem p-Wert im Bayes-Framework. Können verstehen es, in einer umfassenden Weise.

Die Nullhypothese im bayesschen Rahmen geht von einer probability Wahrscheinlichkeitsverteilung nur bei einem bestimmten Wert eines Parameters (z. B. θ=0,5) und einer Wahrscheinlichkeit von Null aus wo., (M1)

Die alternative Hypothese ist, dass alle Werte von θ möglich sind, daher eine flache Kurve, die die Verteilung darstellt. (M2)

Nun sieht die posteriore Verteilung der neuen Daten wie folgt aus.

Bayes-Statistik angepasst Glaubwürdigkeit (Wahrscheinlichkeit) für verschiedene Werte von θ. Es ist leicht zu erkennen,dass sich die Wahrscheinlichkeitsverteilung in Richtung M2 mit einem höheren Wert als M1 verschoben hat, dh M2 ist wahrscheinlicher.,

Der Bayes-Faktor hängt nicht von den tatsächlichen Verteilungswerten von θ ab, sondern von der Größe der Verschiebung der Werte von M1 und M2.

In Panel A (oben gezeigt): Linker Balken (M1) ist die vorherige Wahrscheinlichkeit der Nullhypothese.

In Panel B (gezeigt) ist der linke Balken die hintere Wahrscheinlichkeit der Nullhypothese.

Bayes-Faktor ist definiert als das Verhältnis der hinteren Quoten zu den vorherigen Quoten,

Um eine Nullhypothese abzulehnen, wird eine BF <1/10 bevorzugt.,

Wir können die unmittelbaren Vorteile der Verwendung von Bayes-Faktor anstelle von p-Werten sehen, da sie unabhängig von Absichten und Stichprobengröße sind.

5.4. High Density Interval (HDI)

HDI wird aus der hinteren Verteilung gebildet, nachdem die neuen Daten beobachtet wurden. Da HDI eine Wahrscheinlichkeit ist, gibt der 95% HDI die 95% glaubwürdigsten Werte. Es ist auch garantiert, dass 95 % Werte in diesem Intervall liegen, im Gegensatz zu C. I.

Beachten Sie, wie der 95% HDI in der vorherigen Verteilung breiter ist als die 95% posteriore Verteilung., Dies liegt daran, dass unser Glaube an HDI bei der Beobachtung neuer Daten zunimmt.

Endnotizen

Ziel dieses Artikels war es, Sie dazu zu bringen, über die verschiedenen Arten statistischer Philosophien nachzudenken und darüber, wie einzelne nicht in jeder Situation verwendet werden können.

Es ist höchste Zeit, dass beide Philosophien zusammengeführt werden, um die Probleme der realen Welt zu mildern, indem die Fehler der anderen behoben werden., Teil II dieser Serie konzentriert sich auf die Techniken zur Reduzierung der Dimensionalität unter Verwendung von MCMC-Algorithmen (Markov Chain Monte Carlo). Teil III basiert auf der Erstellung eines bayesischen Regressionsmodells von Grund auf und der Interpretation seiner Ergebnisse in R. Bevor ich also mit Teil II beginne, möchte ich Ihre Vorschläge / Ihr Feedback zu diesem Artikel haben.