Budgetlinie: Hinweise zu Budgetlinie, Raum, Änderungen und Steigung

Die Kenntnis des Konzepts der Budgetlinie oder der sogenannten Budgetbeschränkung ist für das Verständnis der Theorie des Gleichgewichts des Verbrauchers unerlässlich.

Eine höhere Indifferenzkurve zeigt eine höhere Zufriedenheit als eine niedrigere. Daher wird ein Verbraucher in seinem Versuch, seine Zufriedenheit zu maximieren, versuchen, die höchstmögliche Gleichgültigkeitskurve zu erreichen.,

Aber in seinem Streben, immer mehr Waren zu kaufen und damit immer mehr Zufriedenheit zu erzielen, muss er unter zwei Bedingungen arbeiten: Erstens muss er die Preise für die Waren bezahlen und zweitens hat er ein begrenztes Geldeinkommen, mit dem er die Waren kaufen kann. Wie weit er für seine Einkäufe gehen würde, hängt also von den Preisen der Waren und dem Geldeinkommen ab, das er für die Waren ausgeben muss.,

Um das Gleichgewicht des Verbrauchers zu erklären, muss auch die Haushaltslinie, die die Preise der Waren und das Geldeinkommen des Verbrauchers darstellt, in die Indifferenzkurvenanalyse eingeführt werden.

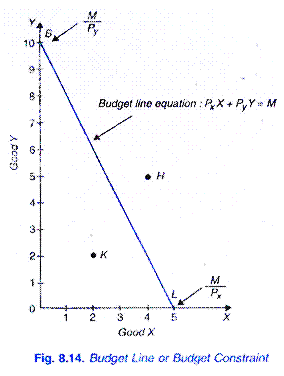
Angenommen, unser Verbraucher hat ein Einkommen von Rs. 50 auf zwei Waren X und Y ausgeben Lassen Preis von gut X auf dem Markt Rs sein. 10 pro Einheit und das von Y Rs. 5 pro Einheit. Wenn der Verbraucher sein gesamtes Einkommen von Rs ausgibt. 50 bei gutem X würde er 5 Einheiten von X kaufen; wenn er sein gesamtes Einkommen von Rs ausgibt., 50 auf gut Y würde er kaufen 10 Einheiten von Y. Wenn eine gerade Linie 5xund 10 gezogen wird, werden wir bekommen, was die Preislinie oder die Budgetlinie genannt wird.

Diese Haushaltslinie zeigt alle Kombinationen von zwei Waren, die der Verbraucher kaufen kann, indem er sein gegebenes Geldeinkommen für die beiden Waren zu ihren gegebenen Preisen ausgibt. Ein Blick auf Abb. 8.14 zeigt, dass mit Rs. 50 und die Preise von X und Y sind Rs 10 und Rs. 5. der Verbraucher kann l0Y und OX oder Stand IX kaufen; oder 6Y und 2X oder 4y und 3X usw.,

Mit anderen Worten, er kann jede Kombination kaufen, die auf der Haushaltslinie mit seinem gegebenen Geldeinkommen und den gegebenen Preisen der Waren liegt. Es sollte sorgfältig darauf hingewiesen werden, dass jede Kombination der beiden Waren wie H (5Y und 4X), die über und außerhalb der angegebenen Haushaltslinie liegt, für den Verbraucher unerreichbar ist.

Aber jede Kombination innerhalb der Haushaltslinie wie K (2X und 2Y) wird für den Verbraucher gut erreichbar sein, aber wenn er eine solche Kombination kauft, wird er nicht sein gesamtes Einkommen von Rs ausgeben. 50., Wenn also davon ausgegangen wird, dass das gesamte gegebene Einkommen für die gegebenen Waren und zu gegebenen Preisen von ihnen ausgegeben wird, muss der Verbraucher aus all jenen Kombinationen wählen, die auf der Haushaltslinie liegen.

Es ist von oben klar, dass Budgetlinie grafisch die Budgetbeschränkung zeigt. Die Kombinationen von Waren, die rechts von der Haushaltslinie liegen, sind unerreichbar, weil das Einkommen des Verbrauchers nicht ausreicht, um diese Kombinationen zu kaufen., Angesichts des Einkommens und der Preise der beiden Waren der Verbraucher sind die Kombinationen von Waren, die links von der Haushaltslinie liegen, erreichbar, dh der Verbraucher kann jeden von ihnen kaufen.

Es ist auch wichtig zu bedenken, dass der Abfangen OB auf der Y-Achse in Fig. 8.14 entspricht der Höhe seines gesamten Einkommens (M) geteilt durch den Preis (PY) der Ware Y. Das heißt, OB = M/PY. Ebenso misst der Intercept OL auf der X-Achse das Gesamteinkommen geteilt durch den Preis der Ware X. Somit ist OL = M / Px.,

Die Haushaltslinie kann algebraisch wie folgt geschrieben werden:

Wobei Px und Py die Preise von Waren X bzw. Y bezeichnen und M für Geldeinkommen steht:

Die obige Haushaltsliniengleichung (1) impliziert, dass angesichts des Geldeinkommens der Waren verbraucher und Preise der beiden Waren, jede Kombination, die auf der Budgetlinie liegt, kostet den gleichen Geldbetrag und kann daher mit dem angegebenen Einkommen gekauft werden., Die Haushaltslinie kann als eine Reihe von Kombinationen von zwei Waren definiert werden, die gekauft werden können, wenn das gesamte gegebene Einkommen für sie ausgegeben wird und seine Steigung gleich dem Negativ des Preisverhältnisses ist.

Budget Raum:

Es sollte sorgfältig verstanden werden, dass die budget gleichung PxX + PyY= M oder Y = M/Py – Px/PyX dargestellt durch die budget linie in Fig. 8.14 beschreibt nur die Budgetlinie und nicht den Budgetbereich., Ein Budgetraum zeigt eine Reihe aller Kombinationen der beiden Waren an, die gekauft werden können, indem das gesamte oder ein Teil des gegebenen Einkommens ausgegeben wird.

Mit anderen Worten, der Budgetraum stellt die für den Verbraucher festgelegte Möglichkeit dar, dh alle Kombinationen von zwei Waren, die er angesichts seiner Budgetbeschränkung kaufen kann. Somit impliziert der Haushaltsraum die Menge aller Kombinationen von zwei Gütern, für die das Einkommen, das für gut X (d. H. P) ausgegeben wird, und das Einkommen, das für gut Y (d. H. PyY) ausgegeben wird, das angegebene Geldeinkommen nicht überschreiten dürfen.,

Daher können wir den Budgetraum algebraisch in der folgenden Form der Ungleichung ausdrücken:

PxX + PyY < M oder M > PxX + PyY

Der Budgetraum wurde grafisch dargestellt in Fig. 8.15 als schattiger Bereich. Der Budgetraum ist der gesamte Bereich, der von der Budgetlinie BL und den beiden Achsen umschlossen wird.

Preisänderungen und Verschiebung der Haushaltslinie:

Nun, was passiert mit der Haushaltslinie, wenn sich entweder die Warenpreise ändern oder sich das Einkommen ändert., Nehmen wir zunächst den Fall der Preisänderungen der Waren. Dies ist in Abb. 8.16. Angenommen, die Haushaltslinie am Anfang ist BL, angesichts bestimmter Preise für Waren X und Y und eines bestimmten Einkommens. Angenommen, der Preis von X fällt, bleiben der Preis von Y und das Einkommen unverändert. Jetzt, mit einem niedrigeren Preis von X kann der Verbraucher mit seinem gegebenen Einkommen mehr Menge von X als zuvor kaufen.

Lassen Sie zum niedrigeren Preis von X das gegebene Einkommen von OL‘ von X, das größer als OL ist., Da der Preis von Y gleich bleibt, kann sich die gekaufte Menge von Gut Y mit demselben gegebenen Einkommen nicht ändern, und infolgedessen wird sich der Punkt B nicht verschieben.Mit dem Preisverfall von gut X, dem Geldeinkommen des Verbrauchers und dem Preis von Y, der konstant bleibt, verschiebt sich die Haushaltslinie nach rechts auf die neue Position BL‘.,

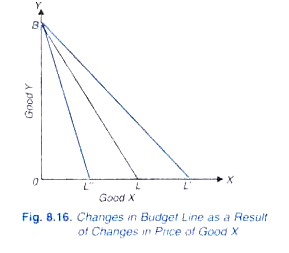
Nun, was wird mit der Budgetlinie passieren (ursprüngliche Budgetlinie BL) wenn der Preis für gut X steigt, bleiben der Preis für gut Y und das Einkommen unverändert. Mit höheren Preis von gut X, kann der Verbraucher kleinere Menge von X kaufen, sagen OL “ als zuvor. Mit dem Preisanstieg von X verschiebt sich die Haushaltslinie also nach links zur neuen Position BL“.

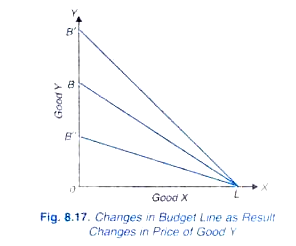
Abbildung 8.,17 zeigt die Änderungen in der Haushaltslinie, wenn der Preis für Gut Y fällt oder steigt, wobei der Preis für X und das Einkommen gleich bleiben. In diesem ist die ursprüngliche Haushaltslinie BL. Da der Preis für gutes Y sinkt und andere Dinge unverändert bleiben,könnte der Verbraucher mit dem gegebenen Geldeinkommen mehr von Y kaufen, und daher wird sich die Haushaltslinie nach LB verschieben. In ähnlicher Weise wird sich die Haushaltslinie mit dem Preisanstieg von Y, der unter anderem konstant ist, unter LB verschieben.,

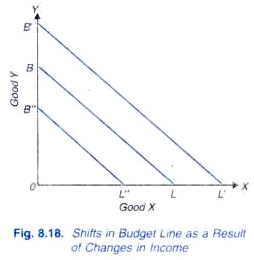
Einkommensänderungen und Verschiebungen in der Haushaltslinie:

Die Frage ist nun, was mit der Haushaltslinie passiert, wenn sich das Einkommen ändert, während die Warenpreise gleich bleiben. Die Auswirkungen von Einkommensänderungen auf die Haushaltslinie sind in Abb. 8.18. Lassen Sie es die ursprüngliche Haushaltslinie sein, angesichts bestimmter Preise von Waren und Einkommen. Wenn das Einkommen der Verbraucher steigt, während die Preise für beide Waren X und y unverändert bleiben, verschiebt sich die Preislinie nach oben (z. B. nach BL‘) und verläuft parallel zur ursprünglichen Haushaltslinie BL.,

Dies liegt daran, dass der Verbraucher mit dem erhöhten Einkommen in der Lage ist, proportional größere Mengen an Gütern X als zuvor zu kaufen, wenn das gesamte Einkommen für X ausgegeben wird, und proportional größere Mengen an Gütern Y als zuvor, wenn das gesamte Einkommen für Y ausgegeben wird Andererseits, wenn das Einkommen des Verbrauchers sinkt, bleiben die Preise für beide Waren X und Y unverändert, verschiebt sich die Haushaltslinie nach unten (z. B. nach B“L“), bleibt aber parallel zur ursprünglichen Preislinie BL.,

Dies liegt daran, dass ein niedrigeres Einkommen eine proportional geringere Menge an Gütern X kauft, wenn das gesamte Einkommen für X ausgegeben wird, und proportional geringere Menge an Gütern Y, wenn das gesamte Einkommen für Y ausgegeben wird

Von oben wird deutlich, dass sich die Haushaltslinie ändert, wenn sich entweder die Warenpreise ändern oder sich das Einkommen des Verbrauchers ändert.

Somit sind die beiden Determinanten der Haushaltslinie:

(a) Die Preise von Waren und

(b) Das Einkommen des Verbrauchers, das für die Waren ausgegeben werden soll.,

Steigung der Haushaltslinie und Preise von zwei Waren:

Es ist auch wichtig zu bedenken, dass die Steigung der Haushaltslinie dem Verhältnis der Preise von zwei Waren entspricht. Dies kann mit Hilfe von Abb. 8.14. Angenommen,das angegebene Einkommen des Verbrauchers ist M und die angegebenen Preise für Waren X und Y sind Px bzw.

Die Steigung der Haushaltslinie BL ist OB / OL. Wir beabsichtigen zu beweisen, dass diese Steigung dem Verhältnis der Preise der Waren X und Y entspricht.,

Die Menge des gekauften Gutes X, wenn das gesamte angegebene Einkommen M dafür ausgegeben wird OL. Daher OL x Px = M

OL = M/Px

Nun ist die Menge des gekauften Gutes Y, wenn das gesamte angegebene Einkommen M dafür ausgegeben wird, OB.

Es ist somit bewiesen, dass die Steigung der Haushaltslinie BL gleich dem Preisverhältnis zweier Waren ist.