Theoretischer Hintergrund
Inhaltsverzeichnis
Einführung
Der Cantilever Beam ist eine der einfachsten Strukturen. Es verfügt über nur eine Unterstützung an einem seiner Enden. Die Stütze ist eine sogenannte feste Stütze, die jede Bewegung, einschließlich vertikaler oder horizontaler Verschiebungen sowie jeglicher Rotationen, hemmt. Das andere Ende wird nicht unterstützt und kann sich daher frei bewegen oder drehen. Dieses freie Ende wird oft als Spitze des Auslegers bezeichnet.,
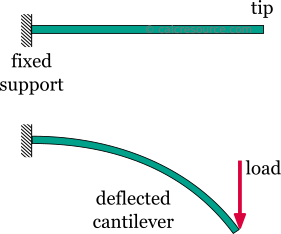
Das Entfernen des Singe-Trägers oder das Einfügen eines internen Scharniers würde den Cantilever-Strahl in einen Mechanismus verwandeln: einen Körper, der sich ohne Einschränkung in eine oder mehrere Richtungen bewegt. Dies ist eine unerwünschte Situation für eine Tragstruktur. Dadurch bietet der Cantilever Beam keine Redundanz in Bezug auf Stützen. Wenn ein lokaler Fehler auftritt, würde die gesamte Struktur zusammenbrechen., Diese Art von Strukturen, die keine Redundanz bieten, werden als kritische oder determinante Strukturen bezeichnet. Im Gegenteil, eine Struktur, die mehr Stützen aufweist, als zur Einschränkung ihrer Bewegungsfreiheit erforderlich sind, wird als redundante oder unbestimmte Struktur bezeichnet. Der Cantilever Beam ist eine determinante Struktur.
Die statische Analyse einer Tragstruktur beinhaltet die Schätzung ihrer inneren Kräfte und Momente sowie ihrer Auslenkungen., Typischerweise sind für eine ebene Struktur mit ebener Belastung die internen Aktionen von Interesse die Axialkraft N, die Querscherkraft V und das Biegemoment M. Bei einem freitragenden Träger, der nur Querbelastungen trägt, ist die Axialkraft immer Null, sofern die Auslenkungen gering sind. Daher ist es ziemlich üblich, axiale Kräfte zu vernachlässigen.,
Die berechneten Ergebnisse auf dieser Seite basieren auf folgenden Annahmen:
- Das Material ist homogen und isotrop (mit anderen Worten, seine Eigenschaften sind in jedem Punkt und in jede Richtung gleich)
- Das Material ist linear elastisch
- Die Lasten werden statisch angelegt (sie ändern sich nicht mit der Zeit)
- Der Querschnitt ist über die gesamte Strahllänge gleich
- Die Auslenkungen sind klein
- Jeder Querschnitt, der anfänglich eben und auch normal zur Längsachse ist, bleibt eben und auch normal zur Umlenkachse., Dies ist der Fall, wenn die Querschnittshöhe ziemlich kleiner als die Trägerlänge ist (10-mal oder mehr) und auch der Querschnitt nicht mehrschichtig ist (kein Sandwichabschnitt).
Die letzten beiden Annahmen erfüllen auch hier die kinematischen Anforderungen an die Euler-Bernoulli-Strahltheorie.
Vorzeichenkonvention
Zur Berechnung der inneren Kräfte und Momente ist an jedem Schnittabschnitt des Balkens eine Vorzeichenkonvention erforderlich., Hier wird Folgendes übernommen:
- Die Axialkraft gilt als positiv, wenn sie eine Spannung am Teil bewirkt
- Die Scherkraft ist positiv, wenn sie eine taktweise Drehung des Teils bewirkt.
- Das Biegemoment ist positiv, wenn es Spannung an der unteren Faser des Balkens und Kompression an der oberen Faser verursacht.
Diese Regeln sind zwar nicht obligatorisch, aber ziemlich universell. Ein anderer Satz von Regeln, wenn konsequent befolgt würde auch die gleichen physikalischen Ergebnisse produzieren.,e, V und Biegemoment, M
Symbole
- E : der Materialelastizitätsmodul (Young-Modul)
- I : das Trägheitsmoment des Querschnitts um die elastische Neutralachse des Biegens
- L : die gesamte Strahllänge
- R : Stützreaktion
- d : Durchbiegung
- M : Biegemoment
- V : Querscherkraft
- \theta : Steigung
li>
Auslegerträger mit gleichmäßig verteilter Last
Die Last w ist über den Auslegerbereich verteilt und weist eine konstante Größe und Richtung auf., Seine Abmessungen sind Kraft pro Länge. Die Gesamtkraft, die auf den freitragenden Balken ausgeübt wird , ist W=Wl, wobei L die Strahllänge ist. Abhängig von den Umständen kann entweder die Gesamtkraft W oder die verteilte Kraft pro Länge w angegeben werden.
Die folgende Tabelle enthält die Formeln, die die statische Reaktion des Cantilever-Strahls unter einer gleichmäßig verteilten Last w beschreiben .
Freitragender Strahl mit Punktkraft an der Spitze
Die Kraft konzentriert sich auf einen einzigen Punkt am freien Ende des Strahls., In der Praxis kann die Kraft jedoch über einen kleinen Bereich verteilt sein, obwohl die Abmessungen dieses Bereichs wesentlich kleiner sein sollten als die freitragende Länge. In der Nähe der Kraftanwendung werden Spannungskonzentrationen erwartet, und infolgedessen ist die von der klassischen Strahltheorie vorhergesagte Reaktion möglicherweise ungenau. Dies ist jedoch nur ein lokales Phänomen. Wenn wir uns vom Kraftort entfernen, werden die Ergebnisse aufgrund des Saint-Venant-Prinzips gültig.,
Die folgende Tabelle enthält die Formeln, die die statische Reaktion des freitragenden Strahls unter einer konzentrierten Punktkraft P beschreiben, die an der Spitze auferlegt wird.
Freitragender Strahl mit Punktkraft an einer zufälligen Position
Die Kraft konzentriert sich in einem einzigen Punkt, irgendwo über die freitragende Länge. In der Praxis kann die Kraft jedoch über einen kleinen Bereich verteilt sein. Um die Kraft jedoch als konzentriert zu betrachten, sollten die Abmessungen des Anwendungsbereichs wesentlich kleiner als die Strahllänge sein., In der näheren Umgebung der Kraft werden Spannungskonzentrationen erwartet und infolgedessen ist die von der klassischen Strahlentheorie vorhergesagte Reaktion möglicherweise ungenau. Dies ist jedoch nur ein lokales Phänomen, und wenn wir uns vom Kraftort entfernen, wird die Diskrepanz der Ergebnisse vernachlässigbar.
Die folgende Tabelle enthält die Formeln, die die statische Reaktion des Auslegerstrahls unter einer konzentrierten Punktkraft P beschreiben, die in einem zufälligen Abstand a von der festen Stütze auferlegt wird.,
Freitragender Strahl mit Punktmoment
In diesem Fall wird ein Moment an einem einzigen Punkt des Strahls überall über die Spannweite verhängt. In der Praxis könnte es sich um ein Kraftpaar oder ein Torsionsglied handeln, das aus der Ebene und senkrecht zum Strahl verbunden ist.
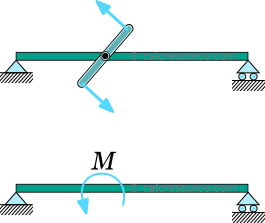
In jedem Fall sollte sich der Momentanwendungsbereich auf eine kleine Länge des Cantilevers ausbreiten, damit er erfolgreich als konzentrierter Moment bis zu einem Punkt idealisiert werden kann., Obwohl in der Nähe des Anwendungsbereichs erwartet wird, dass die vorhergesagten Ergebnisse durch die klassische Strahlentheorie ungenau sind (aufgrund von Spannungskonzentrationen und anderen lokalisierten Effekten), werden die vorhergesagten Ergebnisse vollkommen gültig, wenn wir uns entfernen, wie durch das Saint-Venant-Prinzip angegeben.
Die folgende Tabelle enthält die Formeln, die die statische Reaktion des Auslegerstrahls unter einem konzentrierten Punktmoment M beschreiben, das in einem Abstand a von der festen Stütze auferlegt wird.,
Cantilever beam mit variierender verteilter Last
Die Last wird über die Cantilever-Länge verteilt und hat eine linear variierende Größe, beginnend mit w_1 am festen Träger bis zu w_2 am freien Ende. Die Abmessungen von w_1 und w_2 sind Kraft pro Länge. Die auf den Träger ausgeübte Gesamtkraft beträgt W={L\over2} (w_1+w_2) , wobei L die freitragende Länge ist.
Die Werte w_1 und w_2 können frei zugeordnet werden. Es ist nicht zwingend erforderlich, dass ersteres kleiner als letzteres ist. Sie können sogar negative Werte annehmen (einen oder beide).,
Wenn w_1=0 ist , entsprechen die Formeln in der folgenden Tabelle einer dreieckigen verteilten Last mit zunehmender Größe (Spitze an der Spitze).
Wenn w_2=0 ist , entsprechen die Formeln in der folgenden Tabelle einer dreieckigen verteilten Last mit abnehmender Größe (Spitze am festen Träger).
Die folgende Tabelle enthält die Formeln, die die statische Reaktion des Cantilever-Strahls unter einer variierend verteilten Last von Trapezform beschreiben.,
Freitragende Träger mit trapezförmiger Lastverteilung
Diese Lastverteilung ist typisch für freitragende Träger einer Platte. Die Verteilung sieht aus wie ein rechtes Trapez, mit einem zunehmenden Teil in der Nähe der festen Stütze und einem konstanten Teil, mit einer Größe gleich w , auf der verbleibenden Länge, bis zur Spitze. Die Abmessungen von w sind Kraft pro Länge. Die auf den Träger ausgeübte Gesamtkraft beträgt W=w (L-a/2) , wobei L die freitragende Länge und a die Länge nahe der festen Stütze ist, wobei die Lastverteilung variiert (dreieckig).,
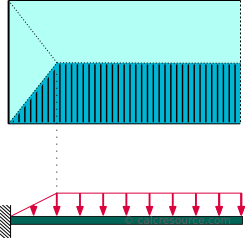
Die folgende Tabelle enthält die Formeln, die die statische Reaktion des Cantilever-Strahls unter einer trapezförmigen Lastverteilung aufgrund einer Platte beschreiben, wie im obigen Schema dargestellt.
Freitragender Balken mit teilweise verteilter gleichmäßiger Last
Die Last wird auf einen Teil der freitragenden Länge mit konstanter Größe w verteilt, während die verbleibende Länge entladen wird. Die Abmessungen von w sind Kraft pro Länge., Die auf den Träger ausgeübte Gesamtkraft beträgt W=w\links (L-a-b\rechts) , wobei L die freitragende Länge und a , b die unbelasteten Längen auf der linken bzw. rechten Seite des Trägers sind.
Die folgende Tabelle enthält die Formeln, die die statische Reaktion des freitragenden Strahls unter einer teilweise verteilten gleichmäßigen Last beschreiben.
Auslegerträger mit teilweise verteilter Trapezlast
Die Last wird auf einen Teil der Auslegerlänge mit linear variierender Größe von w_1 bis w_2 verteilt, während die verbleibende Länge entladen wird., Die Abmessungen von w_1 und w_2 sind Kraft pro Länge. Die auf den Strahl ausgeübte Gesamtkraft beträgt W={L-a-b\over2}(w_1+w_2) , wobei L die Strahllänge und a , b die unbelasteten Längen auf der linken bzw. rechten Seite des Strahls sind.
Die Werte w_1 und w_2 können frei zugeordnet werden. Es ist nicht zwingend erforderlich, dass ersteres kleiner als letzteres ist. Sie können sogar negative Werte annehmen (einen oder beide).
Dies ist die generischen Fall., Die Formeln für teilweise verteilte gleichmäßige und dreieckige Lasten können durch entsprechende Einstellung der Werte von w_1 und w_2 abgeleitet werden . Des Weiteren können durch Setzen von a und b auf Null die jeweiligen Fälle für voll beladene Spannweite abgeleitet werden.
Die folgende Tabelle enthält die Formeln, die die statische Reaktion des freitragenden Strahls unter einer teilweise verteilten trapezförmigen Last beschreiben.,
Schreibe einen Kommentar