Der Satz des Pythagoras

Eine der bekanntesten mathematischen Formeln ist der Satz des Pythagoras, der uns die Beziehung zwischen den Seiten in einem rechtwinkligen Dreieck liefert. Ein rechtwinkliges Dreieck besteht aus zwei Beinen und einer Hypotenuse. Die beiden Beine treffen sich in einem Winkel von 90° und die Hypotenuse ist die längste Seite des rechten Dreiecks und die Seite gegenüber dem rechten Winkel.,

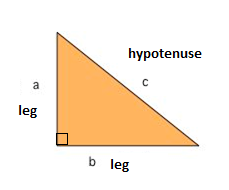
Der Satz von Pythagoras besagt, dass die Beziehung in jedem rechtwinkligen Dreieck lautet:

$$a^{2}+b^{2}=c^{2}$$

Beispiel

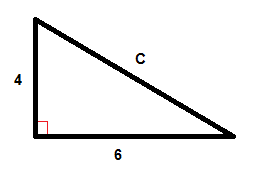
$$C^{2}=6^{2}+4^{2}$$

$$C^{2}=36+16$$

$$C^{2}=52$$

$$C=\sqrt{52}$$

$$C\approx $ $$

Es gibt einige spezielle Arten von rechtwinkligen Dreiecken, wie die 45°-45° rechtwinkligen Dreiecke und das 30°-60° rechtwinklige Dreieck.,

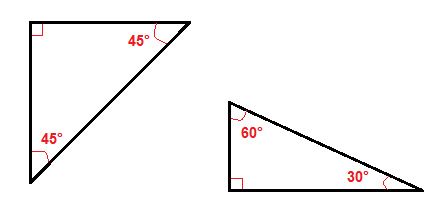
Aufgrund ihrer Winkel ist es einfacher, die Hypotenuse oder die Beine in diesen rechten Dreiecken zu finden als in allen anderen rechten Dreiecken.

In einem 45°-45° rechtwinkligen Dreieck müssen wir nur ein Bein mit √2 multiplizieren, um die Länge der Hypotenuse zu erhalten.

Beispiel

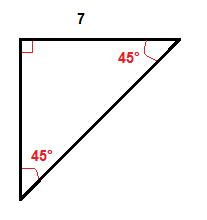
Wir multiplizieren die Länge des Beins, die 7 Zoll mal √2 beträgt, um die Länge der Hypotenuse zu erhalten.

$$7\cdot \sqrt{2}\ca.,9$$

In einem 30°-60° – rechtwinkligen Dreieck können wir die Länge des Beins ermitteln, die dem 30° – Winkel entgegengesetzt ist, indem wir diese Formel verwenden:

$$a=\frac{1}{2}\cdot c$$

Beispiel

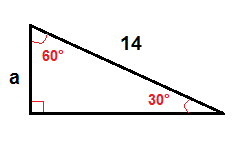
Um a zu finden, verwenden wir die obige Formel.

$$a=\frac{1}{2}\cdot 14$$

$$a=7$$

Video-Lektion

Finden Sie die Seiten dieses rechtwinkligen Dreiecks