Die Binomialverteilung

„Bi“ bedeutet „zwei“ (wie ein Fahrrad hat zwei Räder) … … es geht also um Dinge mit zwei Ergebnissen.,

Werfen wir eine Münze!

Werfen Sie eine faire Münze dreimal … was ist die Chance, zwei Köpfe zu bekommen?,tr>

THH THT TTH TTT

Which outcomes do we want?,

„Zwei Köpfe“ sein kann in beliebiger Reihenfolge: „HHT“, „THH“ und „HTH“ alle haben zwei Köpfe (und ein Endstück).

So erzeugen 3 der Ergebnisse „Zwei Köpfe“.

Wie hoch ist die Wahrscheinlichkeit eines jeden Ergebnisses?,ationen sind (P bedeutet „Wahrscheinlichkeit von“):

• P (Drei Köpfe) = P(HHH) = 1/8
• P (Zwei Köpfe) = P (HHT) + P (HTH) + P (THH) = 1/8 + 1/8 + 1/8 = 3/8
• P (Ein Kopf) = P (HTT) + P (THT) + P (TTH) = 1/8 + 1/8 + 1/8 = 3/8
• P(Null Köpfe) = P(TTT) = 1/8

Wir können dies in Form einer Zufallsvariablen schreiben, X, = „Die Anzahl der Köpfe von 3 Werfen einer Münze“:

• P(X = 3) = 1/8
• P(X = 2) = 3/8
• P(X = 1) = 3/8
• P(X = 0) = 1/8

Und so sieht es als Diagramm aus:

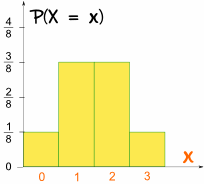
Es ist symmetrisch!,

Formel erstellen

Stellen Sie sich nun vor, wir wollen die Chancen von 5 Köpfen in 9 Würfen: Die Auflistung aller 512 Ergebnisse wird lange dauern!

Also machen wir eine Formel.

Wie können wir in unserem vorherigen Beispiel die Werte 1, 3, 3 und 1 erhalten ?

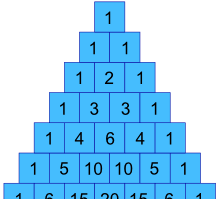
Nun, sie sind tatsächlich in Pascals Dreieck !

Können wir sie mit einer Formel erstellen?

Sicher können wir, und hier ist es:

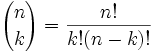
Es wird oft als „n wählen k“

• n = Gesamtzahl
• k = Anzahl wir wollen
• die „!,“bedeutet “ factorial“, zum Beispiel 4! = 1×2×3×4 = 24

Mehr dazu lesen Sie unter Kombinationen und Permutationen.

Versuchen wir es:

Verwenden wir es für eine schwierigere Frage:

Bias!

Bisher waren die Chancen auf Erfolg oder Misserfolg gleich wahrscheinlich.

Aber was ist, wenn die Münzen voreingenommen sind (landen Sie mehr auf einer Seite als auf einer anderen) oder die Auswahl nicht 50/50 ist.

Lassen Sie uns ein Baumdiagramm zeichnen:

Die Fälle „Zwei Hühner“ sind hervorgehoben.

Die Wahrscheinlichkeiten für“ zwei Hühner “ betragen 0,147, da wir jeweils zwei 0,7 s und eine 0,3 multiplizieren. Mit anderen Worten

0.147 = 0.7 × 0.7 × 0.3

Oder mit Exponenten:

= 0,72 × 0,31

Die 0,7 ist die Wahrscheinlichkeit jeder gewünschten Wahl, nennen Sie es p

Die 2 ist die Anzahl der gewünschten Auswahlmöglichkeiten, nennen Sie es k

Und wir haben (bisher):

= pk × 0,31

Die 0.,3 ist die Wahrscheinlichkeit der entgegengesetzten Wahl, also ist es: 1−p

Die 1 ist die Anzahl der entgegengesetzten Entscheidungen, also ist es: n−k

Was uns gibt:

= pk(1-p)(n-k)

Wobei

• p die Wahrscheinlichkeit jeder Wahl ist, die wir wollen
• k ist die Anzahl der Entscheidungen, die wir wollen
• n ist die Gesamtzahl der

Jetzt wissen wir, dass die Wahrscheinlichkeit jedes Ergebnisses 0.147

OK ist. Das war eine Menge Arbeit für etwas, das wir bereits kannten, aber jetzt haben wir eine Formel, die wir für härtere Fragen verwenden können.,

Zusammensetzen

Jetzt wissen wir, wie viele berechnet werden:

n!k!(n-k)!

Und die Wahrscheinlichkeit von jedem:

pk (1-p) (n-k)

Wenn wir multipliziert werden, erhalten wir:

Wichtige Hinweise:

• Die Versuche sind unabhängig,
• Es gibt nur zwei mögliche Ergebnisse in jeder Studie,
• Die Wahrscheinlichkeit eines „Erfolgs“ in jeder Studie ist konstant.,

Quincunx

Spielen Sie mit dem Quincunx (lesen Sie dann Quincunx Explained), um die Binomialverteilung in Aktion zu sehen.

Werfen die Würfel

Ein fairer Würfel wird geworfen, vier mal. Berechnen Sie die Wahrscheinlichkeiten des Erhaltens:

• 0 Twos
• 1 Zwei
• 2 Twos
• 3 Twos
• 4 Twos

In diesem Fall ist n=4, p = P(Zwei) = 1/6

X die Zufallsvariable ‚Anzahl der Zwei aus vier Würfen‘.,

Setzen Sie x = 0 bis 4 in die Formel ein:

P (k aus n) = n!k!(n-k)! pk (1-p) (n-k)

So (bis 4 Dezimalstellen):

Diesmal ist der Graph nicht symmetrisch:

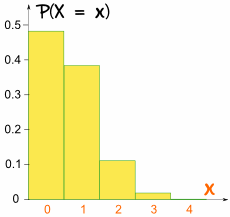
Es ist nicht symmetrisch!

Es ist schief, weil p nicht 0,5

Sportfahrräder

Ihr Unternehmen stellt Sportfahrräder her. 90% bestehen die Endkontrolle (und 10% versagen und müssen repariert werden).

Was ist der erwartete Mittelwert und die Varianz der 4 nächsten Inspektionen?

Berechnen wir zunächst alle Wahrscheinlichkeiten.,

• n = 4,
• p = P(Pass) = 0.9

X ist die Zufallsvariable „Anzahl der Durchläufe von vier Inspektionen“.

Setzen Sie x = 0 bis 4 in die Formel ein:

P (k aus n) = n!k!(n-k)! pk (1-p) (n-k)

Mittelwert, Varianz und Standardabweichung

Berechnen wir den Mittelwert, die Varianz und die Standardabweichung für die Sportfahrradinspektionen.

Es gibt (relativ) einfache Formeln für sie. Sie sind ein wenig schwer zu beweisen, aber sie arbeiten!,

Der Mittelwert oder „Erwartungswert“ ist:

μ = np

Die Formel für die Varianz lautet:

Varianz: σ2 = np (1-p)

Und die Standardabweichung ist die Quadratwurzel der Varianz:

σ = √(np (1-p))