SPSS Correlation Analysis Tutorial (Español)

También vea correlaciones de Pearson-introducción rápida.

• prueba de correlación – ¿Qué es?
• hipótesis nula
• suposiciones
• prueba de correlación en SPSS
• Reporting

prueba de correlación – ¿Qué es?

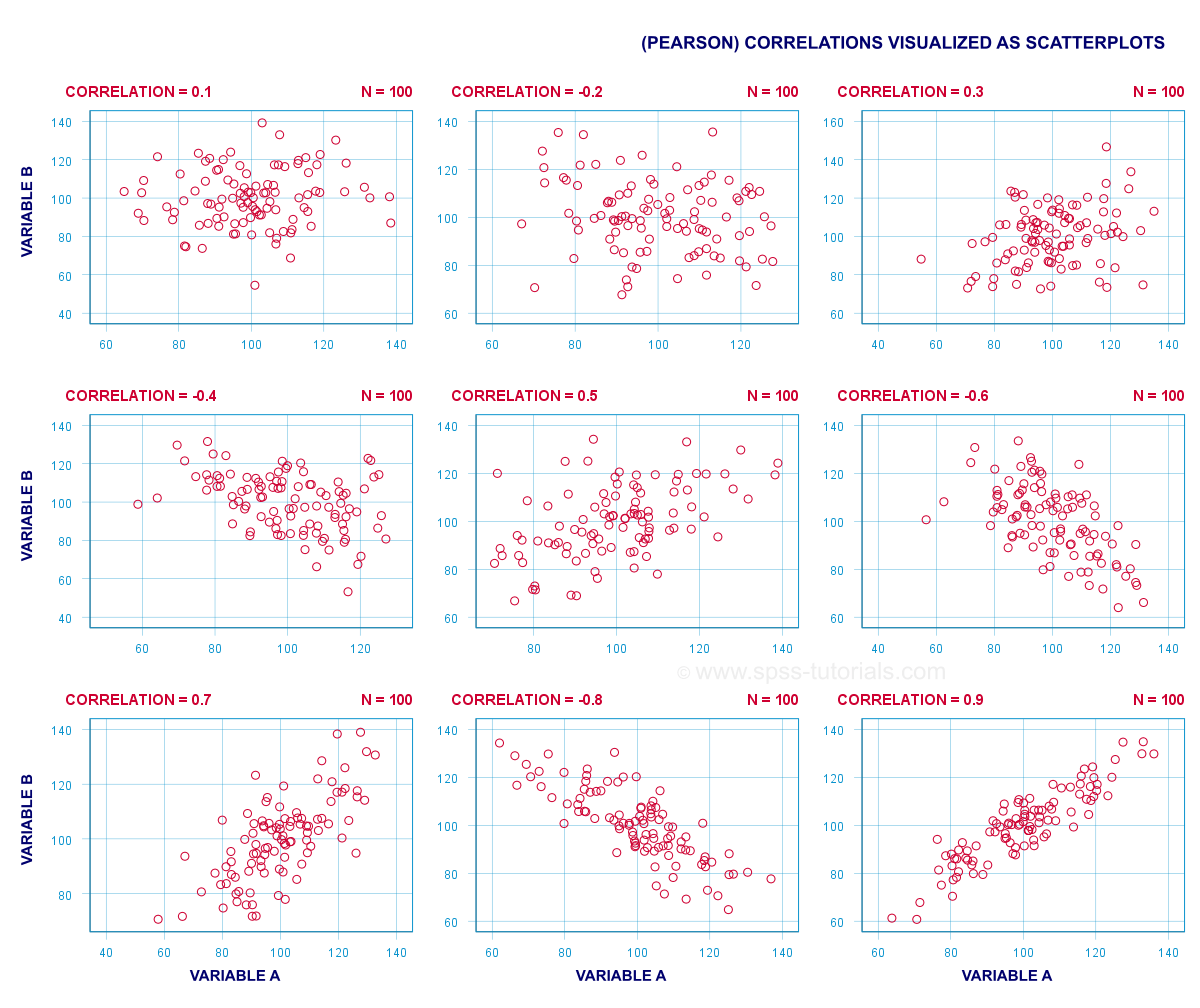
la correlación de Pearson es un número entre -1 y +1 que indica hasta qué punto 2 variables cuantitativas están relacionadas linealmente. Se entiende mejor mirando algunas gráficas de dispersión.,

En resumen,

• una correlación de -1 indica una relación lineal descendente perfecta: las puntuaciones más altas en una variable implican puntuaciones más bajas en la otra variable.
• una correlación de 0 significa que no hay relación lineal entre 2 variables en absoluto. Sin embargo, puede haber una relación no lineal (fuerte) sin embargo.
• una correlación de 1 indica una relación lineal ascendente perfecta: los puntajes más altos en una variable se asocian con puntajes más altos en la otra variable.,

hipótesis nula

una prueba de correlación (generalmente) prueba la hipótesis nula de que la correlación de la población es cero.Los datos a menudo contienen solo una muestra de una población (mucho) más grande: encuesté a 100 clientes (muestra), pero estoy realmente interesado en todos mis 100,000 clientes (población). Los resultados de la muestra suelen diferir un poco de los resultados de la población. Así que encontrar una correlación no cero en mi muestra no prueba que 2 variables están correlacionadas en toda mi población; si la correlación de la población es realmente cero, puedo encontrar fácilmente una pequeña correlación en mi muestra., Sin embargo, encontrar una correlación fuerte en este caso es muy poco probable y sugiere que mi correlación de población no fue cero después de todo.

prueba de correlación-suposiciones

calcular e interpretar los coeficientes de correlación por sí mismos no requiere ninguna suposición. Sin embargo, la prueba de significancia estadística para correlaciones asume

• observaciones independientes;
• normalidad: nuestras 2 variables deben seguir una distribución normal bivariada en nuestra población. Esta suposición no es necesaria para tamaños de muestra de N = 25 o más.,Para tamaños de muestra razonables, el teorema del límite central asegura que la distribución de muestreo será normal.

SPSS-quick Data Check

vamos a ejecutar algunas pruebas de correlación en SPSS ahora. Usaremos adolescentes.sav, un archivo de datos que contiene datos de pruebas psicológicas en 128 Niños entre 12 y 14 años de edad. Parte de su vista variable se muestra a continuación.

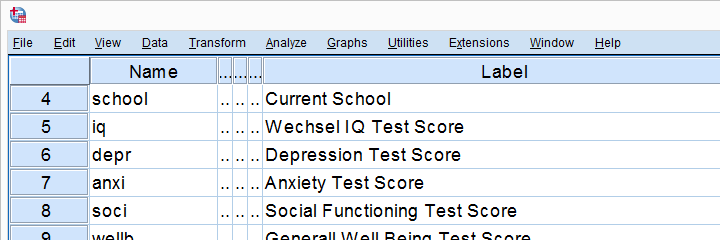
ahora, antes de ejecutar cualquier correlación, primero asegurémonos de que nuestros datos sean plausibles en primer lugar., Dado que las 5 variables son métricas, inspeccionaremos rápidamente sus histogramas ejecutando la sintaxis a continuación.

Salida del histograma

nuestros histogramas nos dicen mucho: nuestras variables tienen entre 5 y 10 valores faltantes. Sus medias están cerca de 100 con desviaciones estándar alrededor de 15, lo cual es bueno porque así es como se han calibrado estas pruebas. Una cosa me molesta, sin embargo, y se muestra a continuación.,

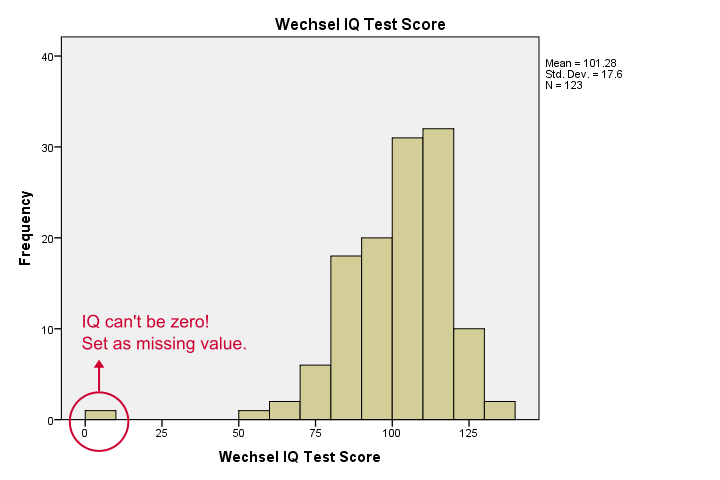
parece que alguien anotó cero en algunas pruebas, lo cual no es plausible en absoluto. Si ignoramos esto, nuestras correlaciones serán severamente sesgadas. Vamos a ordenar nuestros casos, ver lo que está pasando y establecer algunos valores faltantes antes de proceder.

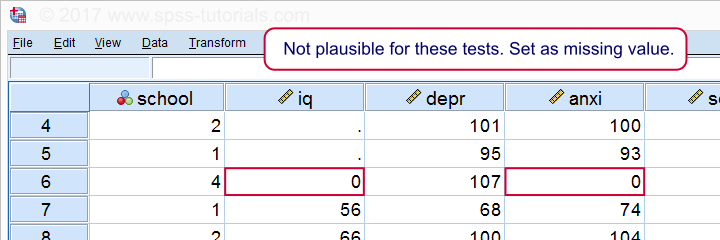
Si ahora volvemos a ejecutar nuestros histogramas, veremos que todas las distribuciones parecen plausibles., Solo ahora debemos proceder a ejecutar las correlaciones reales.

ejecutar una prueba de correlación en SPSS

primero naveguemos a analizarCorrelate Bivariate como se muestra a continuación.

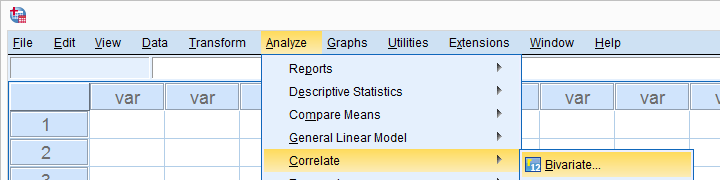
mueva todas las variables relevantes al cuadro variables. Probablemente no quieras cambiar nada más aquí.

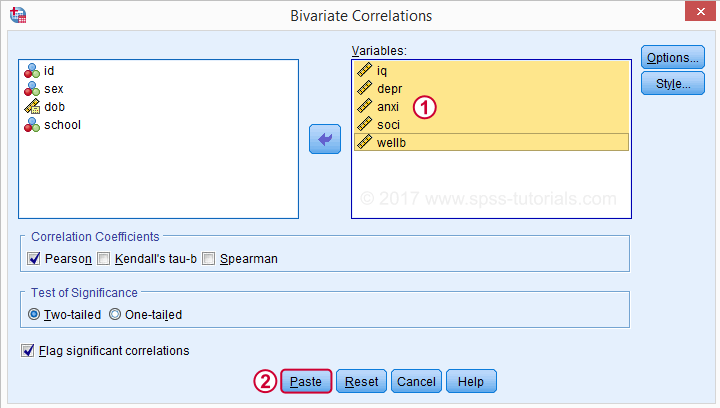
Al hacer clic en Pegar se obtiene la siguiente sintaxis. Vamos a comprobarlo.

sintaxis de correlaciones SPSS

Salida de correlación

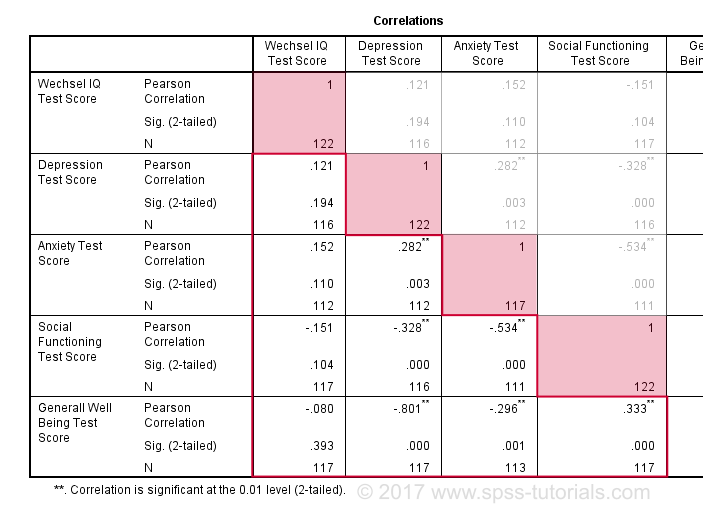
de forma predeterminada, SPSS siempre crea una matriz de correlación completa. Cada correlación aparece dos veces: por encima y por debajo de la diagonal principal. Las correlaciones en la diagonal principal son las correlaciones entre cada variable y sí mismo, por lo que son todas 1 y no son interesantes en absoluto. Las 10 correlaciones por debajo de la diagonal son lo que necesitamos., Como regla general,una correlación es estadísticamente significativa si su «Sig. (2-tailed)» < 0.05.Ahora echemos un vistazo a nuestros resultados: la correlación más fuerte es entre la depresión y el bienestar general : r = -0.801. Se basa en N = 117 niños y su significancia de 2 colas, p = 0,000. Esto significa que hay una probabilidad de 0.000 de encontrar esta correlación de muestra – o una mayor-si la correlación real de la población es cero.tenga en cuenta que el coeficiente intelectual no se correlaciona con nada. Su correlación más fuerte es 0,152 con la ansiedad pero P = 0.,11 por lo que no es estadísticamente significativamente diferente de cero. Es decir, hay una probabilidad de 0.11 de encontrarlo si la correlación de la población es cero. Esta correlación es demasiado pequeña para rechazar la hipótesis nula.
así, nuestras 10 correlaciones indican hasta qué punto cada par de variables están relacionadas linealmente. Finalmente, tenga en cuenta que cada correlación se calcula en un N ligeramente diferente-que va de 111 a 117. Esto se debe a que SPSS utiliza la eliminación por pares de los valores faltantes de forma predeterminada para las correlaciones.,

gráficos de dispersión

estrictamente, debemos inspeccionar todos los gráficos de dispersión entre nuestras variables también. Después de todo, las variables que no se correlacionan podrían estar relacionadas de alguna manera no lineal. Pero para más de 5 o 6 variables, el número de posibles gráficos de dispersión explota, por lo que a menudo omitimos inspeccionarlos. Sin embargo, consulte la herramienta SPSS – crear todas las gráficas de dispersión.
la sintaxis a continuación crea solo una gráfica de dispersión, solo para tener una idea de cómo se ve nuestra relación. Sin embargo, el resultado no muestra nada inesperado.

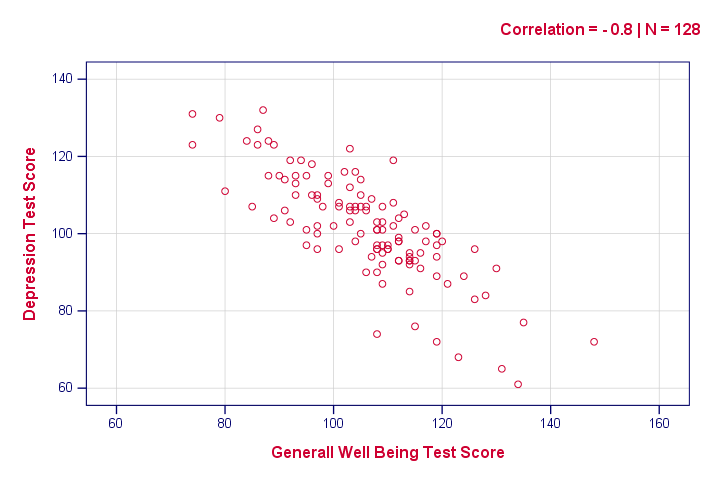
Reporting a Correlation Test

la siguiente figura muestra el formato más básico recomendado por la APA para reportar correlaciones. Es importante asegurarse de que la tabla indica qué correlaciones son estadísticamente significativas en p < 0.05 y quizás p < 0.01. Ver también correlaciones SPSS en formato APA.

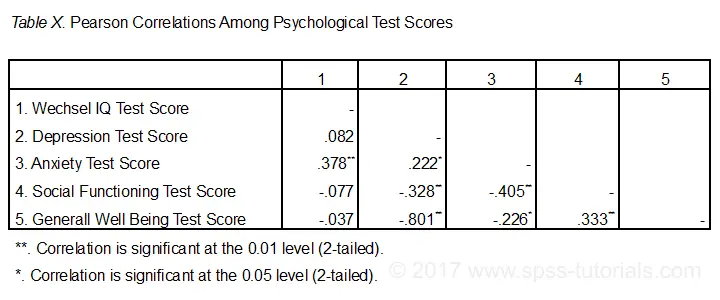
si es posible, también Informe los intervalos de confianza para sus correlaciones., Curiosamente, SPSS no incluye esos. Sin embargo, consulte la herramienta SPSS intervalos de confianza para correlaciones.

Gracias por leer!