L’Intérieur de l’Angle est un angle à l’intérieur d’une forme
un Autre exemple:
les Triangles
Les Angles Intérieurs d’un Triangle ajouter jusqu’à 180°
nous allons essayer un triangle: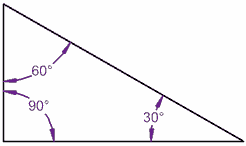
90° + 60° + 30° = 180°
Cela fonctionne pour ce triangle
Maintenant, de l’inclinaison de la ligne de 10°: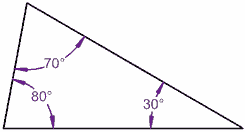
80° + 70° + 30° = 180°
Il fonctionne encore!,
Un angle a augmenté de 10°,
et l’autre est en baisse de 10°
les Quadrilatères (Carrés, etc)
(Un Quadrilatère a 4 côtés droits)
Les Angles Intérieurs d’un Quadrilatère ajouter jusqu’à 360°
Car il y a 2 triangles dans un carré …
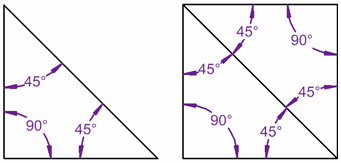
L’intérieur des angles dans un triangle ajouter jusqu’à 180° …
… et pour le carré, ils ajoutent jusqu’à 360° …
… parce que le carré peut être fait de deux triangles!,
Pentagone
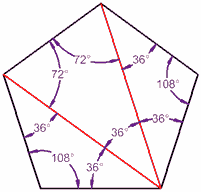
Un pentagone a 5 côtés, et peut être faite à partir de trois triangles, donc vous savez ce qu’ …
…,poule elle est régulière (tous les angles de la même façon), puis chaque angle est de 540° / 5 = 108°
(Exercice: assurez-vous que chaque triangle ajoute jusqu’à 180°, et de vérifier que le pentagone angles intérieurs d’ajouter jusqu’à 540°)
L’Intérieur des Angles d’un Pentagone ajouter jusqu’à 540°
La Règle Générale
Chaque fois que nous ajoutons un côté (triangle, quadrilatère, le quadrilatère de la à la du pentagone, etc), nous ajoutons un autre de 180° à la totale:
Donc, la règle générale est:
Somme des Angles Intérieurs = (n−2) × 180°
Chaque Angle d’un Polygone Régulier) = (n−2) × 180° / n
peut-être un exemple pour vous aider:


Laisser un commentaire