SPSS Correlation Analysis Tutorial (Français)

Voir Aussi Pearson Correlations – introduction rapide.

• Test de corrélation – Qu’est-ce que c’est?
• Hypothèse Nulle
• Hypothèses
• Test de concordance dans SPSS
• Déclaration

la Corrélation Test – Quel Est-Il?

une corrélation (Pearson) est un nombre compris entre -1 et +1 qui indique dans quelle mesure 2 variables quantitatives sont linéairement liées. Il est préférable de comprendre en regardant quelques nuages de points.,

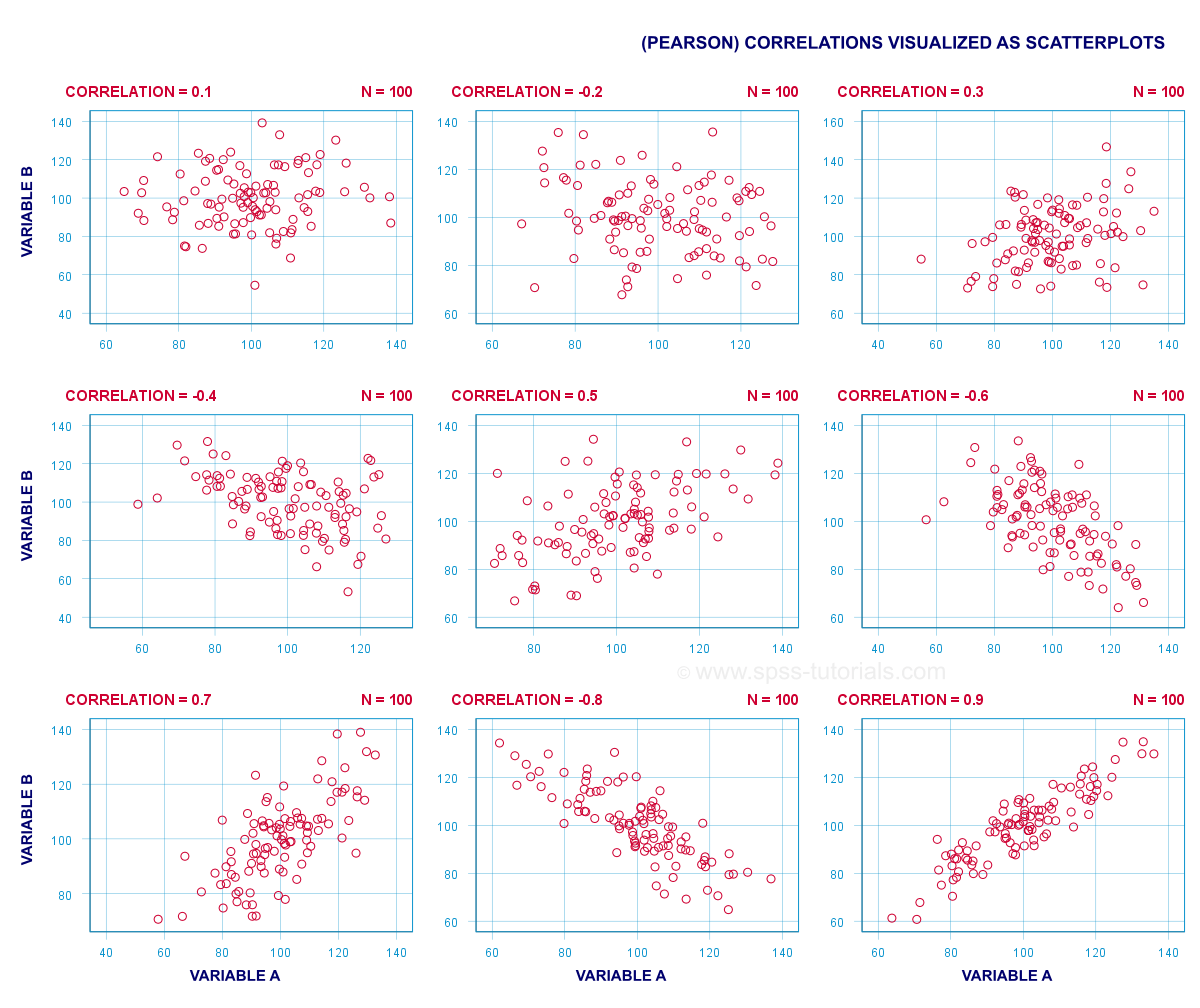
bref,

• une corrélation de -1 indique une parfaite linéaire décroissant relation: des scores plus élevés sur une variable implique des scores plus faibles sur l’autre variable.
• une corrélation de 0 signifie qu’il n’y a aucune relation linéaire entre 2 variables. Cependant, il peut néanmoins y avoir une relation non linéaire (forte).
• une corrélation de 1 indique une relation linéaire ascendante parfaite: des scores plus élevés sur une variable sont associés à des scores plus élevés sur l’autre variable.,

Hypothèse Nulle

Un essai de corrélation (généralement) teste l’hypothèse nulle que la population de corrélation est égal à zéro.Les données ne contiennent souvent qu’un échantillon d’une population (beaucoup) plus importante: j’ai interrogé 100 clients (échantillon) mais je suis vraiment intéressé par tous mes 100 000 clients (population). Les résultats de l’échantillon diffèrent généralement quelque peu des résultats de la population. Donc, trouver une corrélation non nulle dans mon échantillon ne prouve pas que 2 variables sont corrélées dans toute ma population; si la corrélation de population est vraiment nulle, je peux facilement trouver une petite corrélation dans mon échantillon., Cependant, trouver une forte corrélation dans ce cas est très peu probable et suggère que ma corrélation de population n’était pas nulle après tout.

Test de corrélation – hypothèses

Le calcul et l’interprétation des coefficients de corrélation eux-mêmes ne nécessitent aucune hypothèse. Cependant, le test de signification statistique pour les corrélations suppose

• observations indépendantes;
• normalité: nos 2 variables doivent suivre une distribution normale bivariée dans notre population. Cette hypothèse n’est pas nécessaire pour les tailles d’échantillon de N = 25 ou plus.,Pour des tailles d’échantillon raisonnables, le théorème central limite garantit que la distribution d’échantillonnage sera normale.

SPSS – Quick Data Check

exécutons maintenant quelques tests de corrélation dans SPSS. Nous utiliserons des adolescents.sav, un fichier de données qui contient des données de tests psychologiques sur 128 enfants entre 12 et 14 ans. Une partie de sa vue variable est montrée ci-dessous.

maintenant, avant d’exécuter des corrélations, nous allons d’abord nous assurer que nos données sont plausibles en premier lieu., Étant donné que les 5 variables sont métriques, nous inspecterons rapidement leurs histogrammes en exécutant la syntaxe ci-dessous.

sortie de L’histogramme

nos histogrammes nous en disent long: nos variables ont entre 5 et 10 valeurs manquantes. Leurs moyennes sont proches de 100 avec des écarts types autour de 15-ce qui est bien car c’est ainsi que ces tests ont été calibrés. Une chose me dérange, cependant, et c’est montré ci-dessous.,

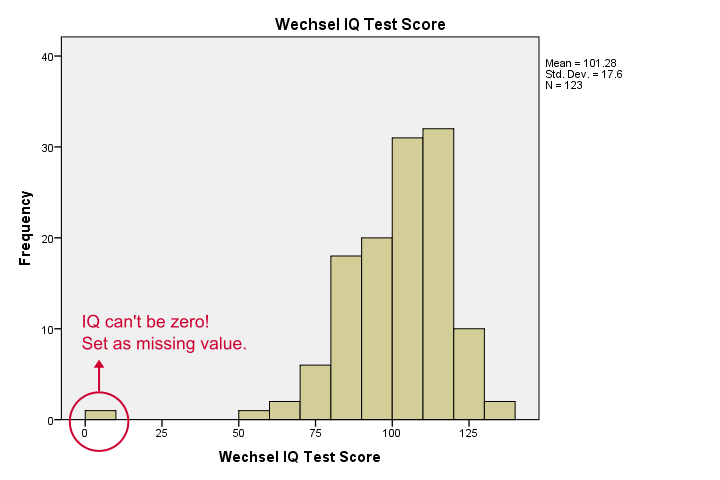
Il semble que quelqu’un ait marqué zéro sur certains tests-ce qui n’est pas du tout plausible. Si nous ignorons cela, nos corrélations seront sévèrement biaisées. Trions nos cas, voyons ce qui se passe et définissons quelques valeurs manquantes avant de continuer.

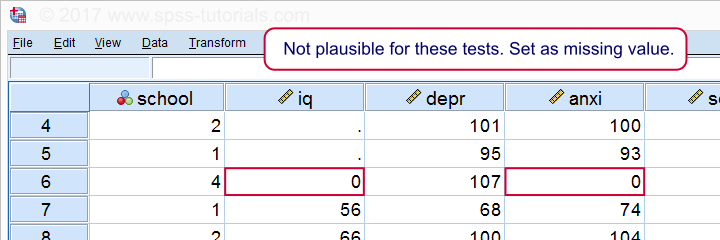
Si nous réexécutons maintenant nos histogrammes, nous verrons que toutes les distributions semblent plausibles., Ce n’est que maintenant que nous devrions procéder à l’exécution des corrélations réelles.

exécution d’un Test de corrélation dans SPSS

naviguons d’abord pour analyser corréler Bivarier comme indiqué ci-dessous.

Déplacer toutes les variables pertinentes dans la zone variables. Vous ne voulez probablement rien changer d’autre ici.

cliquer sur Coller donne la syntaxe ci-dessous. Nous allons l’exécuter.

syntaxe des corrélations SPSS

sortie de corrélation

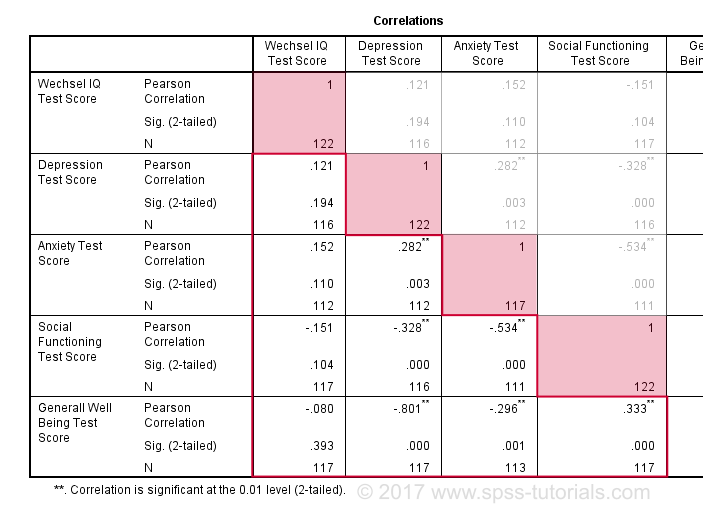
par défaut, SPSS crée toujours une matrice de corrélation complète. Chaque corrélation apparaît deux fois: au-dessus et au-dessous de la diagonale principale. Les corrélations sur la diagonale principale sont les corrélations entre chaque variable et elle-même-c’est pourquoi elles sont toutes 1 et pas intéressantes du tout. Les 10 corrélations sous la diagonale sont ce dont nous avons besoin., En règle générale,une corrélation est statistiquement significative si son « Sig. (2-queue) »< 0.05.Examinons maintenant de près nos résultats: la corrélation la plus forte est entre la dépression et le bien-être global : r = -0.801. Il est basé sur N = 117 enfants et sa signification à 2 queues, p = 0.000. Cela signifie qu’il y a une probabilité de 0,000 de trouver cette corrélation d’échantillon-ou une plus grande – si la corrélation de population réelle est nulle.
notez que le QI ne correspond à rien. Sa corrélation la plus forte est 0.152 avec l’anxiété mais p = 0.,11 donc ce n’est pas statistiquement significativement différent de zéro. Autrement dit, il y a 0,11 chance de le trouver si la corrélation de population est nulle. Cette corrélation est trop faible pour rejeter l’hypothèse nulle.
ainsi, nos 10 corrélations indiquent dans quelle mesure Chaque paire de variables est linéairement liée. Enfin, notez que chaque corrélation est calculée sur un N légèrement différent allant de 111 à 117. En effet, SPSS utilise la suppression par paires des valeurs manquantes par défaut pour les corrélations.,

nuages de points

strictement, nous devrions également inspecter tous les nuages de points parmi nos variables. Après tout, les variables qui ne sont pas corrélées pourraient toujours être liées de manière non linéaire. Mais pour plus de 5 ou 6 variables, le nombre de nuages de points possibles explose, nous ignorons donc souvent leur inspection. Cependant, consultez L’outil SPSS – Create All Scatterplots.
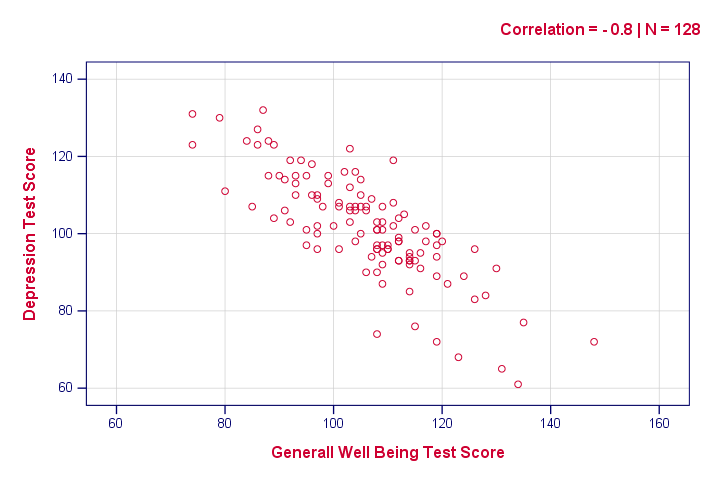
la syntaxe ci-dessous crée un seul nuage de points, juste pour avoir une idée de ce à quoi ressemble notre relation. Le résultat ne montre rien d’inattendu, cependant.

signaler un Test de corrélation

la figure ci-dessous montre le format le plus basique recommandé par L’APA pour signaler les corrélations. Surtout, assurez-vous que le tableau indique les corrélations sont statistiquement significatives à p < 0,05 et peut-être p < 0.01. Voir également les corrélations SPSS au Format APA.

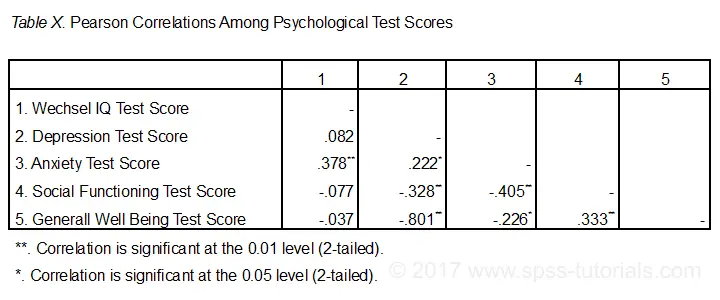
si possible, signalez également les intervalles de confiance pour vos corrélations., Curieusement, SPSS ne les inclut pas. Cependant, consultez L’outil intervalles de confiance SPSS pour les corrélations.

Merci pour la lecture!