most menj vissza a korábbi példát mutatják, 100 fő (amely magában foglalja a 40 terhes nők, a fennmaradó 60 nem terhes nők, mind a férfiak egy kövér hasa), mint terhes vagy nem terhes. A 40 terhes nő közül 30 terhes nő helyesen van besorolva, a fennmaradó 10 terhes nőt pedig a gépi tanulási algoritmus nem terhesnek minősíti. Másrészt a nem terhes kategóriába tartozó 60 ember közül 55 nem terhes, a fennmaradó 5 pedig terhes.,
ebben az esetben TN = 55, FP = 5, FN = 10, TP = 30. A zavart mátrix a következő.

mi a gépi tanulási modell pontossága ehhez az osztályozási feladathoz?,

Pontosság számát jelöli helyesen besorolt adatok esetben a száma összesen adatok esetekben.
ebben a példában a pontosság = (55 + 30)/(55 + 5 + 30 + 10 ) = 0.85 százalékban a pontosság 85% lesz.
A pontosság a legjobb intézkedés?
a pontosság nem feltétlenül jó intézkedés, ha az adatkészlet nem kiegyensúlyozott (mind a negatív, mind a pozitív osztályok eltérő számú adatpéldányt tartalmaznak)., Ezt egy példával magyarázzuk meg.
vegye figyelembe a következő forgatókönyvet: 90 egészséges (negatív) és 10 beteg van valamilyen betegségben (pozitív). Tegyük fel, hogy gépi tanulási modellünk tökéletesen besorolta a 90 embert egészségesnek, de az egészségtelen embereket is egészségesnek minősítette. Mi fog történni ebben a forgatókönyvben? Nézzük meg a zűrzavar mátrixot és derítsük ki a pontosságot?
ebben a példában TN = 90, FP = 0, FN = 10 és TP = 0. A zavart mátrix a következő.,

a pontosság ebben az esetben (90 + 0)/(100) = 0.9 százalékban a pontosság 90 %.
van valami gyanús?
a pontosság ebben az esetben 90%, de ez a modell nagyon rossz, mert mind a 10 egészségtelen ember egészségesnek minősül., Ezzel a példával azt próbáljuk mondani, hogy a pontosság nem jó mutató, ha az adatkészlet kiegyensúlyozatlan. Az ilyen forgatókönyvek pontosságának használata az eredmények félrevezető értelmezését eredményezheti.
tehát most tovább haladunk, hogy megtudjunk egy másik metrikát az osztályozáshoz. Ismét visszatérünk a terhesség osztályozási példájához.
most megtaláljuk a pontosságot (pozitív prediktív érték) az adatpéldányok osztályozásában., A pontosság meghatározása a következő:
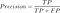
mit jelent a pontosság?
a pontosság ideális esetben 1 (magas) lehet egy jó osztályozó számára. A pontosság csak akkor lesz 1, ha a számláló és a nevező egyenlő, azaz TP = TP + FP, ez azt is jelenti, hogy az FP nulla. Az FP növelésével a nevező értéke nagyobb lesz, mint a számláló, a precíziós érték pedig csökken (amit nem akarunk).
tehát a terhességi példában a pontosság = 30/(30+ 5) = 0.,857
most bemutatunk egy másik fontos mutatót, a visszahívást. Emlékszem, is ismert, mint az érzékenység, vagy a valódi pozitív arány meghatározása a következő:

Emlékszem, hogy ideális esetben 1 (magas) egy jó osztályozó. A visszahívás csak akkor válik 1-re, ha a számláló és a nevező egyenlő i. E TP = TP + FN, ez azt is jelenti, hogy az FN nulla., Az FN növelésével a nevező értéke nagyobb lesz, mint a számláló, a visszahívási érték pedig csökken (amit nem akarunk).
tehát a terhességi példában lássuk, mi lesz a visszahívás.
visszahívás = 30/(30+ 10) = 0.75
tehát ideális esetben egy jó osztályozóban azt akarjuk, hogy mind a pontosság, mind a visszahívás olyan legyen,ami azt is jelenti, hogy az FP és az FN nulla. Ezért szükségünk van egy mutatóra, amely figyelembe veszi mind a pontosságot, mind a visszahívást., F1-pontszám egy mérőszám, amely figyelembe veszi mind a pontosság, mind pedig emlékszem, pedig meghatározása a következő:

F1 Pontszám lesz 1 csak akkor, ha a pontosság, mind pedig emlékszem, hogy mindketten 1. Az F1 pontszám csak akkor lesz magas, ha mind a pontosság, mind a visszahívás magas. Az F1-es pontszám a pontosság és a visszahívás harmonikus átlaga, és jobb mérőszám, mint a pontosság.
a terhességi példában, F1 pontszám = 2* ( 0.857 * 0.75)/(0.857 + 0.75) = 0.799.,
Olvasási lista
a következő érdekes cikk a közös bináris osztályozási mutatóról neptune.ai. a cikk linkje itt érhető el: https://neptune.ai/blog/f1-score-accuracy-roc-auc-pr-auc
Vélemény, hozzászólás?