Druck-und KMT
Die makroskopischen Phänomene von Druck erklärt werden kann in Bezug auf die kinetische molekulare Theorie der Gase. Angenommen, ein Gasmolekül (dargestellt durch eine Kugel) befindet sich in einer Box mit der Länge L (Abbildung 1). Durch die Verwendung der oben dargelegten Annahmen und wenn man bedenkt, dass sich die Kugel nur in x-Richtung bewegt, können wir die Instanz der Kugel untersuchen, die elastisch mit einer der Wände der Box kollidiert.,
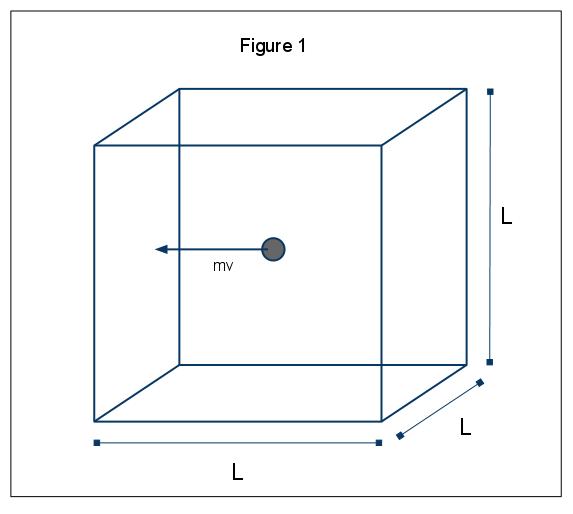
Der Impuls dieser Kollision ist gegeben durch p=mv, in diesem Fall p=mvx, da wir nur die x Dimension betrachten. Die Gesamtimpulsänderung für diese Kollision wird dann durch
\
gegeben, da die Zeitspanne zwischen Kollisionen des Moleküls mit der Wand L / vx beträgt Wir können die Häufigkeit von Kollisionen des Moleküls gegen eine gegebene Wand der Box pro Zeiteinheit als vx/2L angeben., Man kann nun für die Änderung des Impulses pro Zeiteinheit lösen:
\
Das Lösen des Impulses pro Zeiteinheit ergibt die von einem Objekt ausgeübte Kraft (F=ma=p/Zeit)., Mit dem Ausdruck, dass F=mvx2/L man nun für den durch die molekulare Kollision ausgeübten Druck lösen kann, wobei die Fläche als Fläche einer Wand der Box angegeben wird, A=L2:
\
\
Der Ausdruck kann nun in Bezug auf den mit Kollisionen verbundenen Druck aus N Anzahl von Molekülen geschrieben werden:
\
Dieser Ausdruck kann nun angepasst werden, um die Bewegung in x -, y-und z-Richtung zu berücksichtigen, indem die mittlere quadratische Geschwindigkeit für drei Dimensionen und ein großer Wert von N., Der Ausdruck wird nun wie folgt geschrieben:
\
Dieser Ausdruck gibt nun Druck, eine makroskopische Qualität, in Bezug auf atomare Bewegung. Die Bedeutung der obigen Beziehung besteht darin, dass der Druck proportional zur mittleren quadratischen Geschwindigkeit von Molekülen in einem bestimmten Behälter ist. Mit zunehmender Molekulargeschwindigkeit steigt daher auch der auf den Behälter ausgeübte Druck.
Schreibe einen Kommentar