En Indre Vinkel er en vinkel inne i en form
et Annet eksempel:
Trekanter
Det Indre Vinklene i en Trekant legge opp til 180°
La oss prøve en trekant: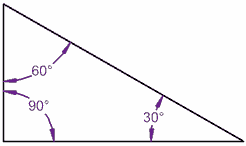
90° + 60° + 30° = 180°
Det fungerer for denne trekanten
Nå tilt en linje ved 10°: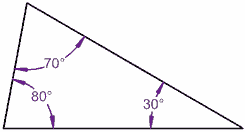
80° + 70° + 30° = 180°
Det fungerer fortsatt!,
En vinkel gikk opp med 10°,
og den andre gikk ned med 10°
Quadrilaterals (Firkanter, etc)
(En Firkant har 4 rett sider)
Det Indre Vinklene i en Firkant legge opp til 360°
Fordi det er 2 trekanter i en firkant …
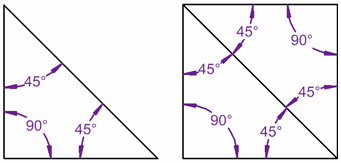
Det indre vinklene i en trekant legge opp til 180° …
… og for den plassen de legger opp til 360° …
… fordi plassen, kan være laget av to trekanter!,
Pentagon
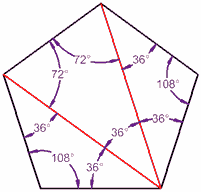
En pentagon har 5 sider, og kan være laget av tre trekanter, slik at du vet hva …
…,a det er vanlig (alle vinkler det samme), så hver vinkel er 540° / 5 = 108°
(Øvelse: sørg for at hver trekant her legger opp til 180°, og sjekk at pentagon ‘ s indre vinklene legge opp til 540°)
Det Indre Vinklene i en Pentagon legge opp til 540°
Generelt
Hver gang vi legger til en side (trekanten for å firkant, firkant til pentagon, etc), legger vi til en annen 180° til totalt:
Slik at den generelle regelen er:
Summen av de Indre Vinklene = (n−2) × 180°
Hver Vinkel (av et Regulært Polygon) = (n−2) × 180° / n
Kanskje et eksempel vil hjelpe:


Legg igjen en kommentar