Een inwendige Hoek is een hoek in een vorm
een Ander voorbeeld:
Driehoeken
Het Interieur van de Hoeken van een Driehoek toevoegen tot 180°
Laten we proberen een driehoek: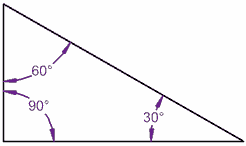
90° + 60° + 30° = 180°
Het werkt voor deze driehoek
Nu tilt een lijn met 10°: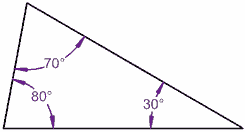
80° + 70° + 30° = 180°
Het werkt nog steeds!,
Een hoek ging 10°omhoog,
en de andere 10°
vierhoeken(vierkanten, enz.)
(een vierhoek heeft 4 rechte zijden)
de binnenhoeken van een vierhoek tellen op tot 360°
omdat er 2 driehoeken in een vierkant zijn…
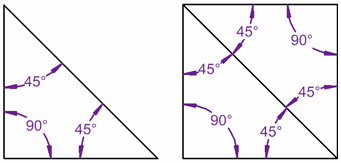
de binnenhoeken in een driehoek bedragen 180° …
… en voor het vierkant tellen ze op tot 360° …
… omdat het vierkant kan worden gemaakt van twee driehoeken!,
Pentagon
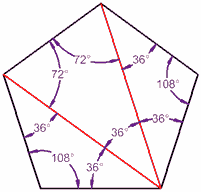
een pentagon heeft 5 zijden en kan worden gemaakt van drie driehoeken, dus je weet wat …
…,kip regelmatig (alle hoeken hetzelfde), dan is elke hoek van de 540° / 5 = 108°
(Oefening: zorg ervoor dat elke driehoek hier voegt tot 180° en controleer dat het pentagon de hoeken oplopen tot 540°)
De Hoeken van een Vijfhoek oplopen tot 540°
De Regel
Elke tijd voegen we een kant (driehoek rechthoekig, vierhoek pentagon, etc), voegen we nog een 180° ten opzichte van het totaal:
Dus de algemene regel is:
de Som van de binnenhoeken = (n−2) × 180°
Elke Hoek (van een Regelmatige Veelhoek) = (n−2) × 180° / n
Misschien een voorbeeld zal helpen:


Geef een reactie