|
Zwei Dreiecke sind kongruent, wenn sie haben:
Aber wir müssen nicht alle drei Seiten und alle drei Winkel kennen …normalerweise reichen drei von sechs aus. |
Es gibt fünf Möglichkeiten zu finden, ob zwei Dreiecke kongruent sind: SSS, SAS, ASA, AAS und HL.,
SSS (Seite, Seite, Seite)
SSS steht für „Seite, Seite, Seite“ und bedeutet, dass wir zwei Dreiecke, bei denen alle drei Seiten gleich.
Zum Beispiel:
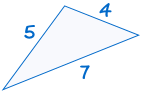 |
ist kongruent zu: | 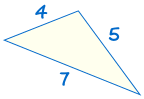 |
(Siehe Lösen von SSS-Dreiecken, um mehr zu erfahren)
Wenn drei Seiten eines Dreiecks gleich drei Seiten eines anderen Dreiecks sind, sind die Dreiecke kongruent.,
SAS (side, angle, side)
SAS steht für „side, angle, side“ und bedeutet, dass wir zwei Dreiecke haben, von denen wir wissen, dass zwei Seiten und der enthaltene Winkel gleich sind.,
Zum Beispiel:
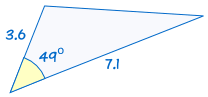 |
ist kongruent zu: | 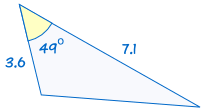 |
(Siehe Lösen von SAS-Dreiecken lesen Sie weiter)
Wenn zwei Seiten und der eingeschlossene Winkel eines Dreiecks gleich den entsprechenden Seiten und dem Winkel eines anderen Dreiecks sind, sind die Dreiecke kongruent.,
ASA (Winkel, Seite, Winkel)
ASA steht für „Winkel, Seite, Winkel“ und bedeutet, dass wir zwei Dreiecke haben, bei denen wir wissen, dass zwei Winkel und die enthaltene Seite gleich sind.,
Zum Beispiel:
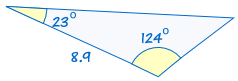 |
ist kongruent zu: | 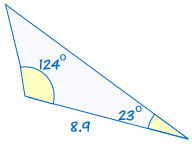 |
(Siehe Lösen) Weitere Informationen)
Wenn zwei Winkel und die eingeschlossene Seite eines Dreiecks den entsprechenden Winkeln und der Seite eines anderen Dreiecks entsprechen, sind die Dreiecke kongruent.,
AAS (Winkel, Winkel, Seite)
AAS steht für „Winkel, Winkel, Seite“ und bedeutet, dass wir zwei Dreiecke haben, bei denen wir wissen, dass zwei Winkel und die nicht enthaltene Seite gleich sind.,
Zum Beispiel:
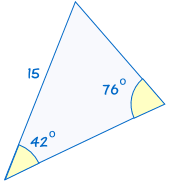 |
ist kongruent zu: | 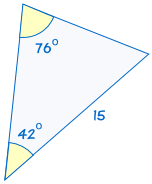 |
(Siehe Lösen von AAS Weitere Informationen)
Wenn zwei Winkel und die nicht enthaltene Seite eines Dreiecks den entsprechenden Winkeln und der Seite eines anderen Dreiecks entsprechen, sind die Dreiecke kongruent.
HL (hypotenuse, leg)
Dieses gilt nur für rechtwinklige Dreiecke!,
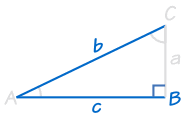 |
oder | 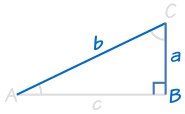 |
HL steht für „Hypotenuse, Bein“ (die längste Seite eines rechtwinkligen Dreiecks wird „Hypotenuse“ genannt, die anderen beiden Seiten werden „legs“genannt)
Es bedeutet, dass wir zwei rechtwinklige Dreiecke mit
- die gleiche Länge der Hypotenuse und
- die gleiche Länge für eines der beiden anderen Beine haben.
Es spielt keine Rolle, welches Bein, da die Dreiecke gedreht werden könnten.,
Zum Beispiel:
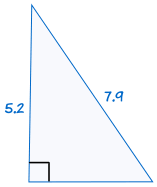 |
ist kongruent zu: | 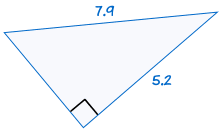 |
(siehe Pythagoras‘ Theorem um mehr zu erfahren)
Wenn die Hypotenuse und ein Bein eines rechtwinkligen Dreiecks gleich der entsprechenden Hypotenuse und dem Bein eines anderen rechtwinkligen Dreiecks sind, sind die beiden Dreiecke kongruent.
Achtung! Verwenden Sie nicht “ AAA “
AAA bedeutet, dass wir alle drei Winkel eines Dreiecks erhalten, aber keine Seiten.,
Dies sind nicht genügend Informationen, um zu entscheiden, ob zwei Dreiecke kongruent sind!
Weil die Dreiecke die gleichen Winkel haben können, aber unterschiedliche Größen haben:
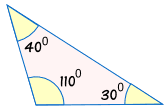 |
ist nicht kongruent zu: | 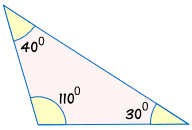 |
Ohne mindestens eine Seite zu kennen, können wir nicht sicher sein, ob zwei Dreiecke kongruent sind.





Schreibe einen Kommentar