en invändig vinkel är en vinkel inuti en form
ett annat exempel:
trianglar
de inre vinklarna i en triangel lägger till upp till 180°
Låt oss prova en triangel: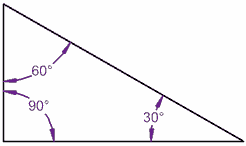
90° + 60° + 30° = 180°
det fungerar för denna triangel
nu luta en linje med 10°:
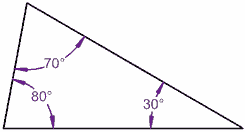
80° + 70° + 30° = 180°
det fungerar fortfarande!,
en vinkel gick upp med 10°,
och den andra gick ner med 10 °
fyrsidiga (kvadrater, etc)
(en fyrsidig har 4 raka sidor)
de inre vinklarna hos en fyrsidig lägger till upp till 360°
eftersom det finns 2 trianglar i en kvadrat …
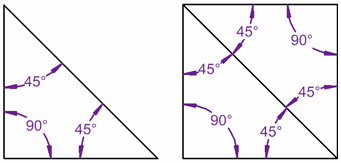
de inre vinklarna i en triangel lägger till upp till 180° …
… och för torget lägger de upp till 360°…
… eftersom torget kan tillverkas av två trianglar!,
Pentagon
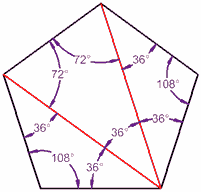
en pentagon har 5 sidor och kan tillverkas av tre trianglar, så du vet vad …
…,då är varje vinkel 540° / 5 = 108°
(övning: se till att varje triangel här lägger till upp till 180° och kontrollera att Pentagons inre vinklar lägger till upp till 540°)
de inre vinklarna i en Pentagon lägger till upp till 540°
den allmänna regeln
varje gång vi lägger till en sida(triangel till fyrsidig, fyrsidig till pentagon, etc) lägger vi till en annan 180° till den totala:
så den allmänna regeln är:
summan av invändiga vinklar = (N−2) × 180°
varje vinkel (av en vanlig polygon) = (n−2) × 180° / n
kanske ett exempel kommer att hjälpa:


Lämna ett svar