In dieser Lektion werden wir die fünf (5) gemeinsamen logischen Verbindungen oder Operatoren konstruieren. Sie gelten als gemeinsame logische Verbindungen, weil sie sehr beliebt, nützlich und immer zusammen unterrichtet werden.
Bevor wir beginnen, schlage ich vor, dass Sie meine andere Lektion überprüfen, in der der Link unten gezeigt wird.
Diese einleitende Lektion über Wahrheitstabellen enthält Grundkenntnisse oder Informationen, die Ihnen helfen, den Inhalt dieser Lektion besser zu verstehen.,
Einführung in Wahrheitstabellen, – anweisungen und-Verknüpfungen
Beginnen wir mit der Auflistung der fünf (5) gemeinsamen logischen Verknüpfungen.
Die fünf (5) gemeinsamen logischen Verknüpfungen oder Operatoren
- Logische Negation
- Logische Verbindung (UND)
- Logische Disjunktion (einschließlich ODER)
- Logische Implikation (bedingt)
- Logische bikonditionelle (doppelte Implikation)
I., Wahrheitstabelle der logischen Negation
Die Negation einer Aussage ist auch eine Aussage mit einem Wahrheitswert, der genau dem der ursprünglichen Aussage entgegengesetzt ist. Zum Beispiel die negation der Aussage steht symbolisch als
~\large{P} oder \large{\neg P}.
~{P} oder {\neg P} wird als“not P“gelesen
Denken Sie daran: Der Negationsoperator, der mit dem Symbol ~ oder \neg bezeichnet wird, nimmt den Wahrheitswert der ursprünglichen Anweisung an und gibt dann das genaue Gegenteil seines Wahrheitswerts aus., Mit anderen Worten, Negation kehrt einfach den Wahrheitswert einer gegebenen Aussage um. Wenn also die Anweisung P wahr ist, ist der Wahrheitswert ihrer Negation falsch. Auf die gleiche Weise, wenn P falsch ist, ist der Wahrheitswert seiner Negation wahr.

II. Die Tabelle der logischen Verbindung
Eine Konjunktion ist eine Art zusammengesetzter Anweisung, die aus zwei Sätzen (auch als einfache Anweisungen bezeichnet) besteht, die vom Operator AND verbunden werden. ,
Das Symbol, das zur Darstellung des Operators UND / oder logische Konjunktion verwendet wird, ist \color{red}\Large{\wedge}. Es sieht aus wie ein umgekehrter Buchstabe V.
Wenn wir zwei einfache Anweisungen P und Q haben und eine zusammengesetzte Anweisung bilden möchten, die vom Operator AND verbunden wird, können wir sie wie folgt schreiben:
\large{P \wedge Q}.
{P \wedge Q} wird als“P und Q.“gelesen
Denken Sie daran: Der Wahrheitswert der zusammengesetzten Anweisung P \wedge Q ist nur wahr, wenn die Wahrheitswerte P und Q beide wahr sind., Andernfalls ist P \wedge Q falsch.
Beachten Sie in der folgenden Wahrheitstabelle, dass, wenn P wahr und Q wahr ist, P \ / Q wahr ist. Die anderen drei Kombinationen der Sätze P und Q sind jedoch falsch.

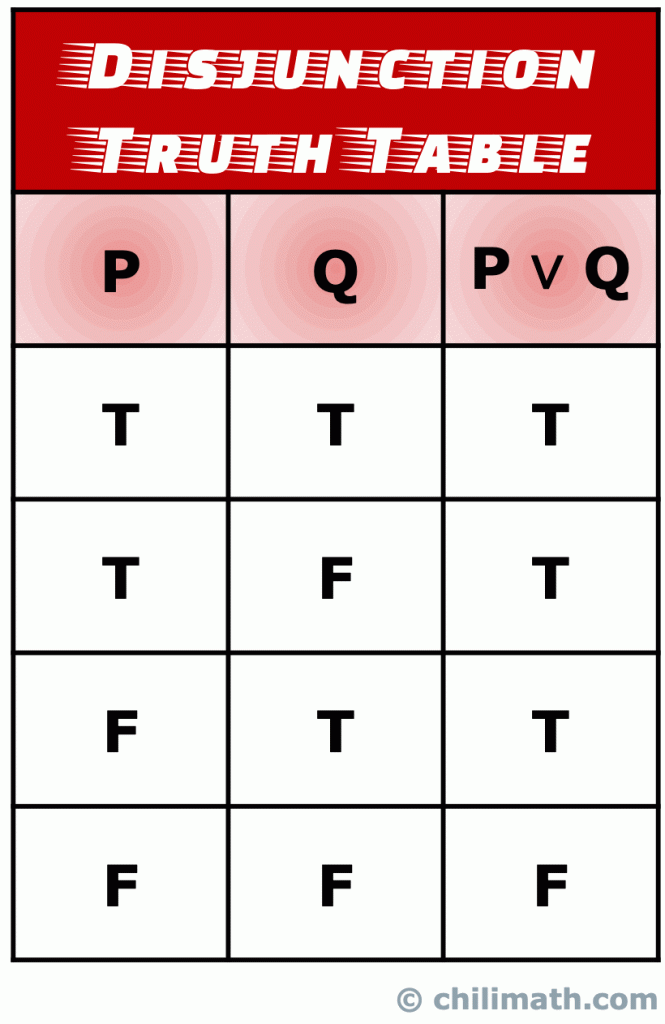
III. Wahrheitstabelle der logischen Disjunktion
Eine Disjunktion ist eine Art zusammengesetzte Anweisung, die aus zwei einfachen Anweisungen besteht, die durch Verbinden der Anweisungen mit dem OR-Operator gebildet werden.
In einer Disjunction-Anweisung ist die Verwendung von OR inklusive. Das bedeutet „das eine oder andere“ oder beides.,
Das Symbol, das zur Darstellung des Operators OR oder logische Disjunktion verwendet wird, ist \color{red}\Large{ \vee }. Es ähnelt dem Buchstaben V des Alphabets.
Zwei sätze P und Q verbunden durch ODER operator zu bilden eine zusammengesetzte anweisung ist geschrieben als:
\large{P \vee Q}.
{P \vee Q} wird als“P oder Q.“ gelesen
Denken Sie daran: Der Wahrheitswert der zusammengesetzten Anweisung P \vee Q ist wahr, wenn der Wahrheitswert der beiden einfachen Anweisungen P und Q wahr ist., Moreso, P \vee Q ist auch wahr, wenn die Wahrheitswerte beider Aussagen P und Q wahr sind. Das einzige Mal, dass die Disjunction-Anweisung P \vee Q falsch ist, tritt auf, wenn die Wahrheitswerte von P und Q falsch sind.
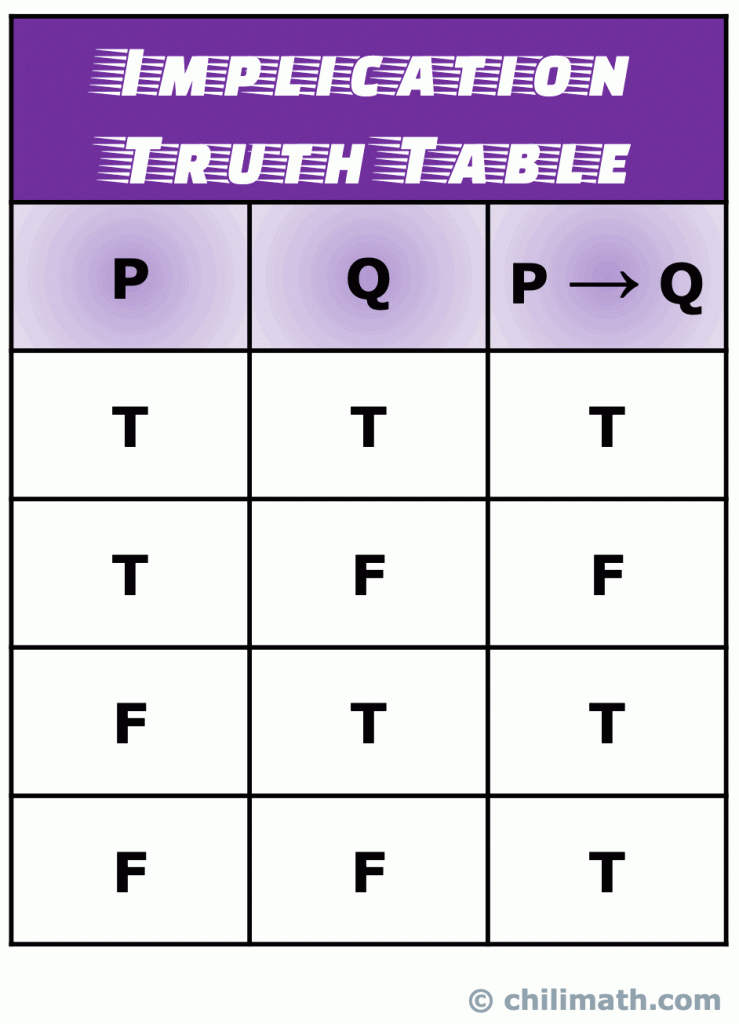
IV. Wahrheitstabelle der logischen Implikation
Eine Implikation (auch als bedingte Anweisung bezeichnet) ist eine Art zusammengesetzter Anweisung, die gebildet wird, indem zwei einfache Anweisungen mit der logischen Implikation verknüpft werden Bindegewebe oder Operator. ,
Das Symbol, mit dem der logische Implikationsoperator dargestellt wird, ist ein nach rechts zeigender Pfeil, also ein Pfeil nach rechts.

Wenn zwei einfache Aussagen P und Q sind verbunden durch die Implikation Betreiber, wir haben:
\Large{P \to Q}.
- wobei P als Hypothese bekannt ist
- wobei Q als Schlussfolgerung bekannt ist
Es gibt viele Möglichkeiten, die Bedingung {P \bis Q} zu lesen., Im Folgenden sind einige der wenigen gemeinsamen.
Denken Sie daran: Der Wahrheitswert der zusammengesetzten Anweisung P \bis Q ist wahr, wenn sowohl die einfachen Anweisungen P als auch Q wahr sind. Moreso, P \zu Q ist immer wahr, wenn P falsch ist. Das einzige Szenario, dass P \zu Q falsch ist, passiert, wenn P wahr ist und Q falsch ist.
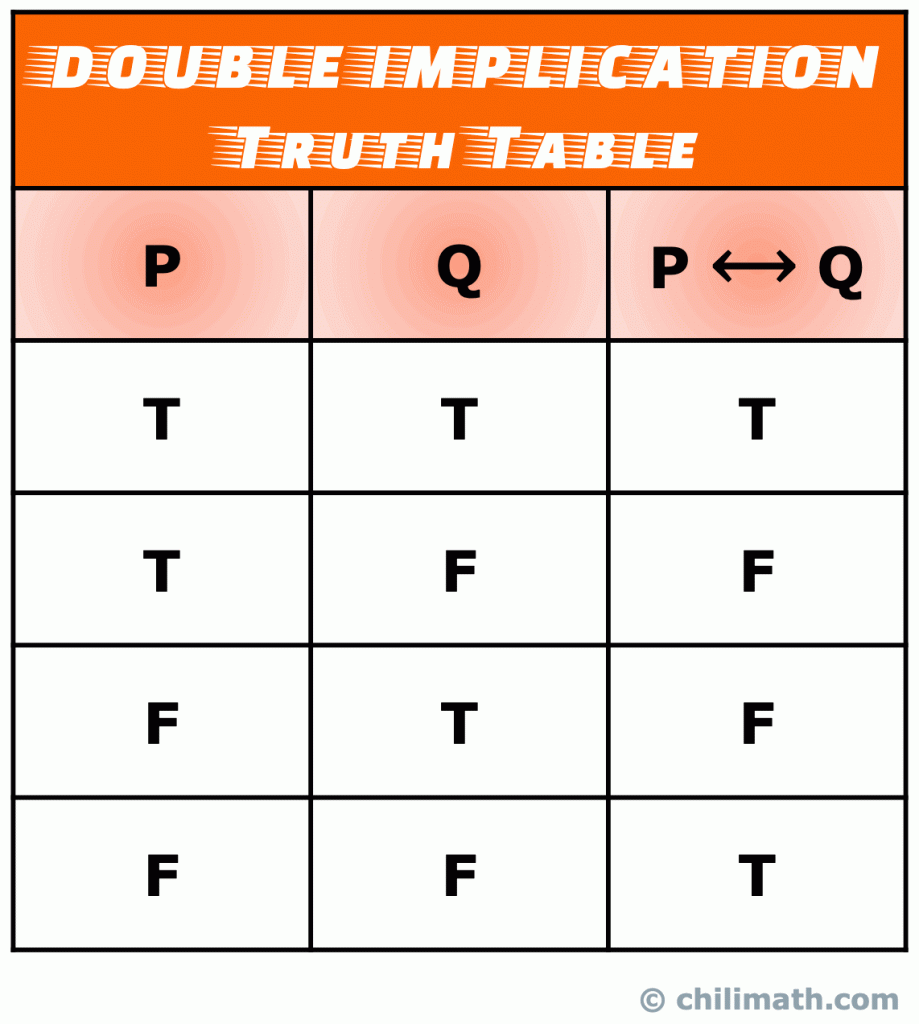
V., Wahrheitstabelle der logischen bikonditionellen oder doppelten Implikation
Eine doppelte Implikation (auch als bikonditionelle Anweisung bezeichnet) ist eine Art zusammengesetzter Anweisung, die durch Verbinden zweier einfacher Anweisungen mit dem bikonditionellen Operator gebildet wird. Eine Biconditional-Anweisung ist wirklich eine Kombination aus einer bedingten Anweisung und ihrer Umkehrung.
Der bikonditionelle Operator wird mit einem Doppelpfeil bezeichnet.,

Wenn Sie zwei einfache Anweisungen (auch als molekulare Anweisungen bezeichnet) mit dem bikonditionellen Operator verbinden, erhalten wir:
\Large{P \leftrightarrow Q}
{P \leftrightarrow Q} wird als „P wenn und nur wenn Q.,“
- wobei P als Vorläufer
- wobei Q als Folge
bekannt ist Denken Sie daran: Der Wahrheitswert der bikonditionellen Anweisung P \leftrightarrow Q ist wahr, wenn sowohl einfache Anweisungen P als auch Q wahr oder beide falsch sind. Andernfalls ist P \ leftrightarrow Q falsch.
Möglicherweise interessieren Sie sich auch für:
Einführung in Wahrheitstabellen, – anweisungen und logische Verknüpfungen
Converse, Inverse und Kontrapositive einer bedingten Anweisung
Schreibe einen Kommentar