koniske afsnit: et afsnit (eller skive) gennem en kegle.vidste du, at ved at tage forskellige skiver gennem en kegle kan du oprette en cirkel, en ellipse, en parabola eller en hyperbola?,

Cones

Circle
straight through
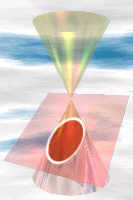
Ellipse
slight angle

Parabola
parallel to edge
of cone

Hyperbola
steep angle
So all those curves are related!
Focus!,
kurverne kan også defineres ved hjælp af en lige linje og et punkt (kaldet directri.og focus).
Når vi måler distance:
- fra fokus til et punkt på kurven, og
- vinkelret fra directrix til dette punkt
de to afstande vil altid være de samme forhold.
- for en ellipse er forholdet mindre end 1
- For en parabola er forholdet 1, så de to afstande er ens.,
- For en hyperbel, forholdet er større end 1
Kort
At forholdet ovenfor er kaldt “excentricitet”, så kan vi sige, at alle keglesnit afsnit er:
“alle punkter, hvis afstand til fokus er lig
at excentricitet gange afstanden til directrix”
For:
- 0 < excentricitet < 1 vi får en ellipse
- excentricitet = 1 en parabel, og
- excentricitet > 1 en hyperbel.,
en cirkel har en e .centricitet på nul, så e .centriciteten viser os, hvordan “un-cirkulær” kurven er. Jo større e .centriciteten er, desto mindre buet er den.
Latus Endetarmen
latus endetarmen (nej, det er ikke en uhøflig ord!) løber parallelt med directri and og passerer gennem fokus. Dens længde er:
- I en parabel, der er fire gange brændvidden
- I en cirkel, er det diameter
- I en ellipse, er 2b2/a (hvor a og b er den ene halvdel af større og mindre diameter).,
Her er en ellipses hovedakse og mindre akse.
Der er et fokus og directri.på hver side (dvs. et par af dem).,
Ligninger
Når den er placeret som på en x-y graf, ligningen for en ellipse er:
x2a2 + y2b2 = 1
Det særlige tilfælde, som af en cirkel (hvor radius=a=b):
x2a2 + y2a2 = 1
Og for en hyperbel det er:
x2a2 − y2b2 = 1
Generelle Ligning
Vi kan lave en ligning, der dækker alle disse kurver.,
fordi de er plane kurver (selvom de er skåret ud af det faste stof), er vi kun nødt til at beskæftige os med kartesiske (“.” og “y”) koordinater.
men disse er ikke lige linjer, så bare “and” og “y” vil ikke gøre … vi skal gå til næste niveau og have:
- 22 og y2,
- og også. (uden y), y (uden.),
- together og Y sammen (.y)
- og et konstant udtryk.
Der skal det gøre det!
og hver enkelt har brug for en faktor (a,b,C osv.)…,
Så den generelle ligning, der dækker alle keglesnit sektioner er:
![]()
Og fra denne ligning kan vi skabe ligninger for den cirkel, ellipse, parabel og hyperbel.






Skriv et svar