Conic sektioner

Conic avsnitt: en sektion (eller skiva) genom en kon.

Cones

Circle
straight through

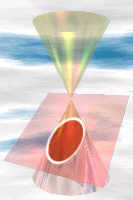
Ellipse
slight angle

Parabola
parallel to edge
of cone

Hyperbola
steep angle

So all those curves are related!

Focus!,

kurvorna kan också definieras med en rak linje och en punkt (kallad directrix och fokus).

När vi mäter avståndet:

• från fokus till en punkt på kurvan, och
• vinkelrätt från directrix till den punkten

de två avstånden kommer alltid att vara samma förhållande.

• för en ellips är förhållandet mindre än 1
• för en parabola är förhållandet 1, Så de två avstånden är lika.,
• för en hyperbola är förhållandet större än 1

excentricitet

det förhållandet ovan kallas ”excentricitet”, så vi kan säga att alla koniska avsnitt är:

för:

• 0< excentricitet< 1 vi får en ellips,
• excentricitet = 1 en parabola, och
• excentricitet> 1 en hyperbola.,

en cirkel har en excentricitet på noll, så excentriciteten visar oss hur ”un-circular” kurvan är. Ju större excentricitet, desto mindre krökt är det.

Latus Rectum

latus rectum (nej, det är inte ett oförskämt ord!) löper parallellt med directrix och passerar genom fokus. Dess längd:

• i en parabola, är fyra gånger brännvidden
• i en cirkel, är diametern
• i en ellips, är 2b2 / a (där A och b är hälften av större och mindre diameter).,

här är huvudaxeln och den mindre axeln hos en ellips.

det finns ett fokus och directrix på varje sida (dvs ett par av dem).,

ekvationer

När den placeras så här i ett X-y − diagram är ekvationen för en ellips:

x2a2 + y2b2 = 1

det speciella fallet för en cirkel (där radius=a=b):

x2a2 + y2a2 = 1

och för en hyperbola är det:

x2a2-y2b2 = 1

allmän ekvation

vi kan göra en ekvation som täcker alla dessa kurvor.,

eftersom de är plankurvor (även om de skärs ut ur det fasta) behöver vi bara hantera kartesiska (”x” och ”y”) koordinater.

men det här är inte raka linjer, så bara ”x” och ”y” kommer inte att göra … vi måste gå till nästa nivå och ha:

• x2 och y2,
• och även x (utan y), y (utan x),
• X och y tillsammans (xy)
• och en konstant term.

där, det borde göra det!

och var och en behöver en faktor (A,B,C etc) …,

så den allmänna ekvationen som täcker alla koniska sektioner är:

och från den ekvationen kan vi skapa ekvationer för cirkeln, ellipsen, parabolen och hyperbola.