sección cónica: una sección (o rebanada) a través de un cono.

Cones

Circle
straight through
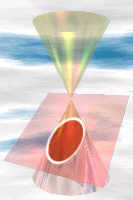
Ellipse
slight angle

Parabola
parallel to edge
of cone

Hyperbola
steep angle
So all those curves are related!
Focus!,
Las curvas también pueden definirse mediante una línea recta y un punto (llamado la directriz y el foco).
Cuando medimos la distancia:
- desde el foco a un punto de la curva, y
- perpendicularmente desde la directriz a ese punto
las dos distancias siempre será la misma proporción.
- para una elipse, la relación es menor que 1
- para una parábola, la relación es 1, por lo que las dos distancias son iguales.,
- Para una hipérbola, el ratio es mayor que 1
Excentricidad
Que la relación anterior es llamado la «excentricidad», por lo que podemos decir que la sección cónica es:
«todos los puntos cuya distancia al foco es igual a
a la excentricidad veces la distancia a la directriz»
Para:
- 0 < excentricidad < 1 se obtiene una elipse,
- excentricidad = 1 una parábola, y
- excentricidad > 1 una hipérbola.,
un círculo tiene una excentricidad de cero, por lo que la excentricidad nos muestra cuán «no circular» es la curva. Cuanto mayor es la excentricidad, menos curvada es.
Latus Recto
El latus recto (no, no es una palabra grosera!) corre paralelo a la directriz y pasa a través del foco. Su longitud:
- En una parábola, es cuatro veces La Longitud focal
- en un círculo, es el diámetro
- en una elipse, es 2b2 / a (donde a y b son la mitad del diámetro mayor y menor).,
Aquí es el eje mayor y el eje menor de una elipse.
hay un foco y una directriz en cada lado (es decir, un par de ellos).,
Ecuaciones
Cuando se coloca así en un gráfico x-y, la ecuación de una elipse es:
x2a2 + y2b2 = 1
El caso especial de un círculo (que radius=a=b):
x2a2 + y2a2 = 1
Y para una hipérbola es:
x2a2 − y2b2 = 1
Ecuación General
podemos hacer una ecuación que cubre todas estas curvas.,
debido a que son curvas planas (aunque cortadas del sólido) solo tenemos que tratar con coordenadas cartesianas («x» E «y»).
pero estas no son líneas rectas, por lo que solo «x» E «y» no bastarán … tenemos que ir al siguiente nivel, y tiene:
- x2 y y2
- y también x (sin y), y (sin x),
- x e y juntos (xy)
- y un término constante.
allí, que debe hacerlo!
y cada uno necesita un factor (A,B, c, etc.)…,
así que la ecuación general que cubre todas las secciones cónicas es:
![]()
y a partir de esa ecuación podemos crear ecuaciones para el círculo, Elipse, Parábola e hipérbola.






Deja una respuesta