Conic-osio: osa (tai viipale) kartion läpi.

Cones

Circle
straight through
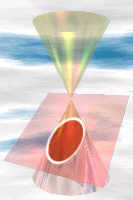
Ellipse
slight angle

Parabola
parallel to edge
of cone

Hyperbola
steep angle
So all those curves are related!
Focus!,
käyrät voidaan määritellä myös käyttämällä suora ja piste (kutsutaan johtosuoran ja focus).
Kun me mitata etäisyys:
- painopiste on piste, käyrä, ja
- kohtisuoraan päässä johtosuoran, että kohta
kahden etäisyydet on aina sama suhde.
- Esimerkiksi ellipsi, suhde on alle 1
- Varten paraabeli, suhde on 1, joten kaksi etäisyydet ovat yhtä suuret.,
- a hyperbeli, suhde on suurempi kuin 1
Eksentrisyys
Että suhde edellä on nimeltään ”eksentrisyys”, niin voimme sanoa, että kaikki kartioleikkauksen on:
”kaikki pisteet, joiden etäisyys painopiste on tasa –
epäkeskisyys kertaa etäisyys directrix”
Varten:
- 0 < eksentrisyys < 1 saadaan ellipsi,
- eksentrisyys = 1 paraabeli, ja
- eksentrisyys > 1 hyperbeli.,
ympyrän eksentrisyys on nolla, joten eksentrisyys näyttää, miten ”un-circular” käyrä on. Mitä suurempi eksentrisyys, sitä vähemmän kaareva se on.
Latus Peräsuolen
latus peräsuolen (ei, se ei ole ruma sana!) kulkee rinnakkain directrixin kanssa ja kulkee fokuksen läpi. Sen pituus:
- Vuonna paraabeli, on neljä kertaa polttoväli
- ympyrä on halkaisijaltaan
- ellipsin, on 2b2/a (missä a ja b ovat puolet suuria ja pieniä halkaisijaltaan).,
Tässä on pääakselin ja pieniä akselin suuntainen ellipsi.
kummallakin puolella on focus ja directrix (eli pari niistä).,
Yhtälöt
Kun sijoittaa kuin tämä x-y kuvaaja, ellipsin yhtälö on:
x2a2 + y2b2 = 1,
erikoistapauksena ympyrä (jossa säde=a=b):
x2a2 + y2a2 = 1,
Ja hyperbeli on:
x2a2 − y2b2 = 1,
Yleiset Yhtälö
Emme voi tehdä yhtälö, joka kattaa kaikki nämä käyrät.,
Koska ne ovat koneen käyrät (vaikka leikata pois kiinteä) me vain täytyy käsitellä Loogiseksi (”x” ja ”y”) – Koordinaatit.
Mutta nämä eivät ole suoria viivoja, joten vain ”x” ja ”y” ei tehdä … meidän täytyy mennä seuraavalle tasolle, ja on:
- x2 ja y2,
- ja myös x (ilman y), y (ilman x),
- x ja y yhteen (xy)
- ja jatkuva aikavälillä.
There, that should do it!
ja jokainen tarvitsee tekijän (A,B,C jne.)…,
Niin yleinen yhtälö, joka kattaa kaikki conic pääluokat on:
![]()
Ja yhtälöstä voimme luoda yhtälöt ympyrä, ellipsi, paraabeli ja hyperbeli.






Vastaa