Sections coniques

section conique: une section (ou tranche) à travers un cône.

Cones

Circle
straight through

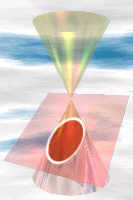
Ellipse
slight angle

Parabola
parallel to edge
of cone

Hyperbola
steep angle

So all those curves are related!

Focus!,

Les courbes peuvent également être définis à l’aide d’une ligne droite et un point (appelé la directrice et de se concentrer).

Lorsque nous mesurons la distance:

• du foyer à un point de la courbe, et
• perpendiculairement de la directrice à ce point

les deux distances seront toujours le même rapport.

• Pour une ellipse, le rapport est inférieur à 1
• Pour une parabole, le rapport est 1, donc les deux distances sont égales.,
• Pour une hyperbole, le ratio est supérieur à 1

Excentricité

Que le ratio ci-dessus est appelé le « excentricité », on peut donc dire que toute conique est:

Pour:

• 0 < excentricité < 1, on obtient une ellipse,
• excentricité = 1 une parabole, et
• excentricité > 1, une hyperbole.,

Un cercle a une excentricité de zéro, donc l’excentricité nous montre à quel point la courbe est « non circulaire ». Plus l’excentricité est grande, moins elle est incurvée.

Latus Rectum

Le latus rectum (non, ce n’est pas un mot impoli!) s’exécute parallèlement à la directrice et traverse le focus. Sa longueur:

• Dans une parabole, soit quatre fois la longueur focale
• Dans un cercle, c’est le diamètre
• Dans une ellipse, est 2b2/a (où a et b sont la moitié de la majeure et la mineure de diamètre).,

Voici le grand axe et le petit axe de l’ellipse.

Il y a un foyer et directrice de chaque côté (c’est à dire une paire d’entre eux).,

les Équations

Lorsqu’il est placé comme sur un graphique x-y, l’équation d’une ellipse est:

x2a2 + y2b2 = 1

Le cas particulier d’un cercle (où radius=a=b):

x2a2 + y2a2 = 1

Et pour une hyperbole c’est:

x2a2 − y2b2 = 1

Équation Générale

On peut faire une équation qui couvre toutes ces courbes.,

Parce que ce sont des courbes planes (même si elles sont découpées dans le solide), nous n’avons qu’à traiter les coordonnées cartésiennes (« x » et « y »).

Mais ce ne sont pas des lignes droites, donc juste « x » et « y » ne feront pas l’affaire … nous avons besoin pour passer au niveau suivant, et disposent de:

• x2 et y2,
• et x (sans y), y (sans x),
• x et y ensemble (xy)
• et un terme constant.

Là, ça devrait le faire!

Et chacun a besoin d’un facteur (A,B,C, etc.) …,

Donc l’équation générale qui couvre toutes les coniques est:

Et à partir de cette équation, nous pouvons créer des équations pour le cercle, ellipse, parabole et hyperbole.