kúpos szakasz: egy szakasz (vagy szelet) egy kúpon keresztül.

Cones

Circle
straight through
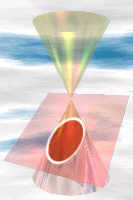
Ellipse
slight angle

Parabola
parallel to edge
of cone

Hyperbola
steep angle
So all those curves are related!
Focus!,
a görbék egy egyenes és egy pont (directrix és focus) segítségével is meghatározhatók.
amikor a távolságot mérjük:
- a fókusztól a görbe egy pontjáig, és
- merőlegesen a directrixtől a pontig
a két távolság mindig azonos arány lesz.
- egy ellipszis esetében az arány kisebb, mint 1
- egy parabola esetében, az arány 1, tehát a két távolság egyenlő.,
- egy hiperbola, ez az arány nagyobb, mint 1
Különcség
Ez az arány felett az úgynevezett “különcség”, így azt mondhatjuk, hogy minden conic szakasz:
“az összes pontot, akinek a távolság, hogy a fókusz egyenlő
a különcség alkalommal a távolság a directrix”
A:
- 0 < különcség < 1 kapunk egy ellipszis,
- különcség = 1 egy parabola, vagy
- különcség > 1 egy hiperbola.,
egy kör excentricitása nulla, tehát az excentricitás megmutatja nekünk, hogy a görbe “kör alakú”. Minél nagyobb az excentricitás, annál kevésbé ívelt.
Latus Rectum
a latus rectum (nem, ez nem durva szó!) párhuzamosan fut a directrixszel és áthalad a fókuszon. Hossza:
- egy parabolában a
- kör fókusztávolságának négyszerese, az ellipszisben a
- átmérője 2B2 / a (ahol a és b a fő-és kisebb átmérő fele).,
itt egy ellipszis főtengelye és kisebb tengelye.
mindkét oldalon van fókusz és directrix (azaz egy pár).,
Egyenletek
Amikor elhelyezett, mint ezt egy x-y grafikon, az egyenlet egy ellipszis van:
x2a2 + y2b2 = 1
A különleges esetben, ha a kör (ahol radius=a=b):
x2a2 + y2a2 = 1
egy hiperbola van:
x2a2 − y2b2 = 1
Általános Egyenlet
lehet, hogy egy egyenlet, ami fedezi ezeket a görbéket.,
mivel síkgörbék (annak ellenére, hogy ki vannak vágva a szilárd anyagból), csak a derékszögű (“x” és “y”) koordinátákkal kell foglalkoznunk.
de ezek nem egyenes vonalak, így csak ” x ” és ” y ” nem fog működni … a következő szintre kell lépnünk:
- x2 és y2,
- , valamint X (Y nélkül), y (x nélkül),
- x és y együtt (xy)
- és egy állandó kifejezés.
ott, hogy meg kell csinálni!
és mindegyiknek szüksége van egy tényezőre (a,B,C stb.)…,
tehát az összes kúpos szakaszt lefedő általános egyenlet a következő:
![]()
és ebből az egyenletből egyenleteket hozhatunk létre a kör, ellipszis, parabola és hyperbola számára.






Vélemény, hozzászólás?